Theoretical Background of Shear Area Calculation
The shear area is a calculated reduction of a cross-sectional area. By using this value, you can consider the shear deformation when determining the internal forces. In contrast to the effective shear area of EN 1993‑1‑1, the shear areas calculated here will only be used to determine the internal forces. Therefore, the shear area of EN 1993‑1‑1 applies for the stress calculation. The reduction of the cross-sectional area results from different distribution of the material law and from the cross-section equilibrium, which leads to a contradiction. This contradiction follows from the hypothesis that the cross-sections remain the same, although the cross-section would be actually subjected to warping when the shear force effect occurs. Therefore, the shear area is introduced into the strength of materials. The derivation of this shear area is described below.
Equalization of the strain energy II* for member element dx
Derivation:
When calculating a rectangle, the result is the shear correction factor κ. This factor indicates to what extent the cross-sectional area must be reduced.
Example of rectangle:
For simple cross-section types, it is possible to conclude the shear area directly. Some of the shear correction factors are:
Rectangle: 0.833
I-beam: ~ Aweb
The comparison of the numerical values shows that you always have to pay attention to the cross-section type when considering the shear deformation. The shear correction factors vary within a wide range, depending on whether there are solid cross-sections, thin-walled open cross-sections, or thin-walled closed cross-sections.
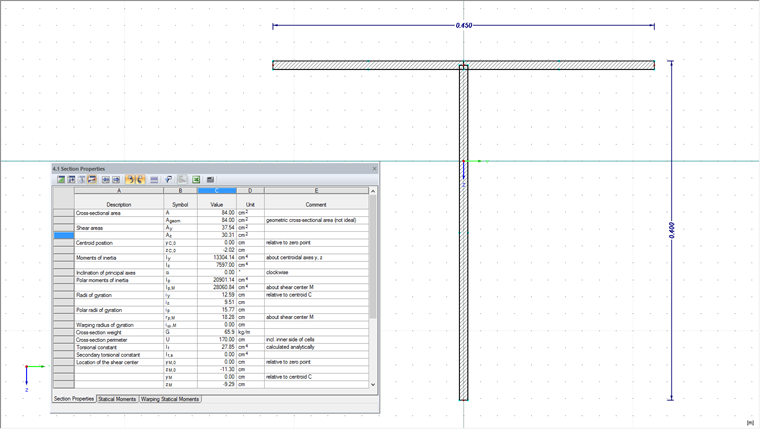
Example of T-Section
The calculation of shear areas for simple cross-sections is thus very easy. For example, if there is only a T-section, SHAPE-THIN determines the shear area for this cross-section automatically.
Analytical solution for shear area calculation:
EN 1993-1-3 
to DIN 18800-2 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
