14751x

001405

Dipl.-Ing. (FH) Stefan Frenzel

20. Februar 2017

Schubflächenberechnung mit DUENQ

Für die Bemessung von Querschnitten werden in der Regel viele verschiedene Querschnittswerte benötigt. In RFEM und RSTAB sind alle dazu benötigten Werte für normierte Querschnitte in der Querschnittsdatenbank vorhanden und man kann diese zur direkten Bemessung heranziehen. Handelt es sich dagegen um nicht normgerechte Querschnitte, so gibt es mit DUENQ die Möglichkeit, auch diese Querschnitte zu verwenden. Über eine einfache Geometrieeingabe können alle benötigten Querschnittswerte ermittelt werden. In folgendem Beispiel wird die Berechnung der Schubfläche anhand eines konkreten Beispiels durchgeführt.

Theoretischer Hintergrund der Schubflächenberechnung

Die Schubfläche ist eine berechnete Reduzierung der Querschnittsfläche. Mit Hilfe dieses Werts kann man die Schubverformung bei der Ermittlung der Schnittgrößen berücksichtigen. Im Gegensatz zur wirksamen Schubfläche der DIN EN 1993-1-1 wird die hier berechnete Schubfläche nur für die Schnittgrößenermittlung verwendet. Für eine Spannungsberechnung findet daher die wirksame Schubfläche der DIN EN 1993-1-1 Anwendung. Die Reduzierung der Querschnittsfläche resultiert aus dem unterschiedlichen Verlauf des Stoffgesetzes und dem Gleichgewicht im Querschnitt, was zu einem Widerspruch führt. Die Ursache für diesen Widerspruch ist die Hypothese vom eben bleiben der Querschnitte, da sich der Querschnitt in Wirklichkeit verwölben würde, wenn eine Querkraftwirkung eintritt. Aus diesem Grund führt man in der Festigkeitslehre die Schubfläche ein. Die Herleitung dieser Schubfläche wird im Folgenden beschrieben.

Gleichsetzen der Formänderungsenergie II* für ein Stabelement dx

Herleitung:

\begin{array}{l} \int_{A} \frac{τ^{2} (z)}{2 \cdot G} dA = \int_{A_{s}} \frac{τ_{m}^{2}}{2 \cdot G} {dA}_{s} = \frac{Q^{2}}{2 \cdot G \cdot A_{s}} \\ \frac{1}{2 \cdot G} \int_{A} {[\frac{Q \cdot S_{y} (z)}{I_{y} \cdot b (z)}]}^{2} dA = \frac{1}{2 \cdot G} \cdot \frac{Q^{2}}{A_{s}} \\ dA = b (z) dz \\ A_{s} = A_{sz} = \frac{I_{y}^{2}}{\int_{z_{o}}^{z_{u}} \frac{S_{y}^{2} (z)}{b (z)} d z} \\ Q = Q_{z} \to A_{sz} \\ Q = Q_{y} \to A_{sy} \end{array}

Formel 1

Bei der Berechnung eines Rechteckes ergibt sich der sogenannte Schubkorrekturfaktor κ. Dieser Faktor gibt an wie stark die Querschnittsfläche reduziert werden muss.

Beispiel Rechteck:

\begin{array}{l} I_{y} = \frac{b \cdot h^{3}}{12} \\ b (z) = b \\ S_{y} (z) = b \int_{- \frac{h}{s}}^{z} \bar{z} d \bar{z} = - \frac{b}{2} \cdot (\frac{h^{2}}{4} - z^{2}) \\ - \frac{h}{2} \leq z \leq \frac{h}{2} \\ \int_{z_{o}}^{z_{u}} S_{y}^{2} (z) dz = \int_{- \frac{h}{s}}^{\frac{h}{2}} \frac{b^{2}}{4} \cdot (\frac{h^{4}}{16} - \frac{1}{2} \cdot h^{2} \cdot z^{2} z^{4}) dz = \frac{b^{2} \cdot h^{5}}{120} \\ A_{s} = \frac{120 \cdot b^{2} \cdot h^{6} \cdot b}{144 \cdot b^{2} \cdot h^{5}} = \frac{5}{6} \cdot b \cdot h = \frac{5}{6} \cdot A \\ κ = \frac{5}{6} \end{array}

Formel 2

Für einfache Querschnittstypen lässt sich so direkt auf die Schubfläche schließen. Nachfolgend sind einige Schubkorrekturfaktoren genannt:
Rechteck: 0,833
I-Träger: ~ A_Steg

Der Vergleich der Zahlenwerte zeigt, dass man im Falle einer Berücksichtigung der Schubdeformation genau beachten muss, welche Profilform vorliegt. Die Schubkorrekturfaktoren schwanken in einem weiten Bereich, je nachdem, ob es sich um Vollquerschnitte, dünnwandige offene oder dünnwandige geschlossene Querschnitte handelt.

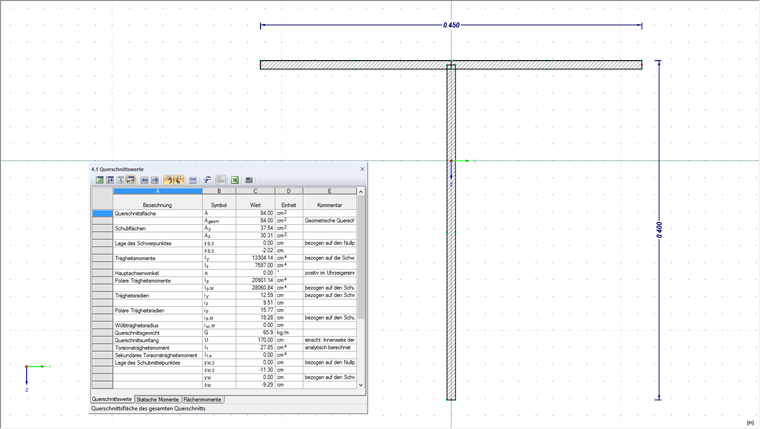
Beispiel eines T-Profils

Die Schubflächen für einfache Querschnitte lassen sich somit sehr einfach berechnen. Hat man nun beispielsweise einen T-Querschnitt, dann ermittelt DUENQ automatisch die Schubfläche dafür.

Eingabe in DUENQ

Analytische Lösung zur Schubflächenberechnung:

\begin{array}{l} I_{y} = 13.304 {cm}^{2} \\ z_{m} = 8, 786 cm \\ b (z) = 1 cm \\ h = 40 cm \\ d = 45 cm \\ S_{y 1} = b (z) \cdot (h - z_{m} - z) \cdot (\frac{h - z_{m} - z}{2} z) \\ S_{y 2} = b (z) \cdot d \cdot - (z_{m} - b (z)) \\ A_{sz} = \frac{I_{y}^{2}}{\int_{- 30, 124}^{8, 786} \frac{S_{y 1} (z)^{2}}{b (z)} dz \int_{9, 286}^{8, 786} \frac{S_{y 2} (z)^{2}}{b (z)} dz} = 30, 17 {cm}^{2} \end{array}

Formel 3

Autor

Herr Frenzel beschäftigt sich mit der Entwicklung im Bereich Dynamik. Außerdem bearbeitet er Anwenderfragen im Kundensupport.

Links

Querschnittswerte-Programme...

;