Teoretické pozadí výpočtu smykové plochy
Smyková plocha se vypočítá jako redukce plochy průřezu. Daná hodnota umožňuje zohlednit deformaci smykem při výpočtu vnitřních sil. Na rozdíl od účinné smykové plochy podle EN 1993-1-1 se zde spočítaná smyková plocha použije pouze pro výpočet vnitřních sil. Při výpočtu napětí se tak uvažuje účinná smyková plocha podle 1993-1-1. Redukce průřezové plochy plyne z rozdílného průběhu materiálového modelu a z rovnováhy v průřezu, což vede k rozporu. Příčinou rozporu je hypotéza zachování rovinnosti průřezu, protože ve skutečnosti by při působení posouvající síly došlo k deplanaci průřezu. Z tohoto důvodu se v nauce o pružnosti a pevnosti zavádí smyková plocha. Odvození smykové plochy popisujeme níže.
Rovnice pro energii změny tvaru II* u prutového prvku dx
Odvození:
Při výpočtu obdélníku dostaneme takzvaný smykový korekční faktor κ, který udává, do jaké míry je průřezovou plochu třeba redukovat.
Příklad obdélníku:
U jednoduchých typů průřezu tak lze vyvodit smykovou plochu přímo. Níže uvádíme některé smykové korekční součinitele:
Obdélník: 0,833
I-nosník: ~ Astojina
Při porovnání hodnot se ukazuje, že v případě zohlednění deformace smykem je nezbytné brát v úvahu tvar průřezu. Smykové korekční součinitele kolísají v širokém rozmezí v závislosti na tom, zda se jedná o plné průřezy, tenkostěnné otevřené anebo tenkostěnné uzavřené průřezy.
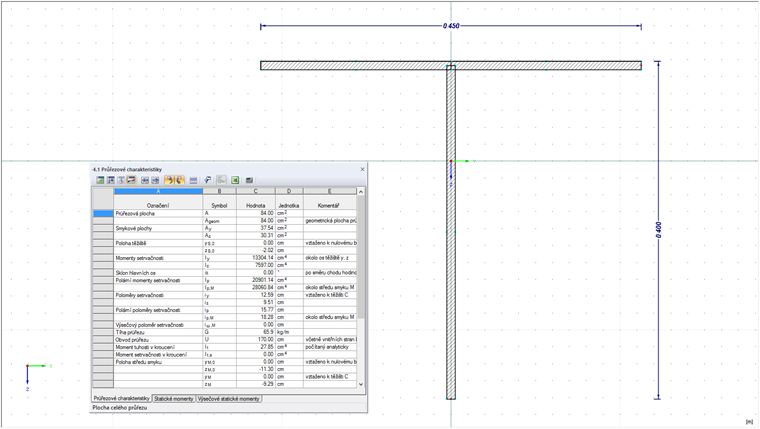
Příklad T-profilu
Smykové plochy lze tedy u jednoduchých průřezů velmi snadno spočítat. Pokud máme například T-průřez, program SHAPE-THIN stanoví smykovou plochu automaticky.
Analytické řešení výpočtu smykové plochy:
.png?mw=350&hash=83397b9718189d605563213de7c48c3b3b18b064)
EN 1993-1-3 
DIN 18800-2 
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
