The effects of wind surround structures, causing forces on walls and sometimes entering buildings if openings exist. The complex architecture of buildings and the requirements from standards for wind make the determination of wind loads one of the main challenges for structural engineers.
Standard and Application Area
The harmonization of standards in Europe has made EC 1 the current standard in many European countries. Eurocode 1 lays down the rules and calculation methods for wind action on buildings less than 200 m tall. EN 1991‑1‑4 also specifies the rules for common chimneys, lattice towers, and bridges (road bridges, craneways, and walkways). Contrary to other Eurocodes, each country has its own National Annex for EC 1. There are, among others, the wind zones (geographical map) and other coefficients.
Pressure Coefficient – General
Each wall of a building is exposed to wind on two faces (the internal and external faces). Wind pressure on the building is either dampened or amplified, depending on the size of the surface the wind is applied to, its openings, and the type of impact on the faces (overpressure or depression). For any structure, we recommend determining these two effects: external pressure and internal pressure.
As many buildings are assumed to be closed, the internal pressure of wind may be negligible.
Internal Pressure Coefficient – Cpi
The internal pressure coefficient cpi depends on the size and layout of the openings in the building. Here, we are talking about permanent openings (such as gaps, chimney ducts, and so on).
If, on at least two faces of a building (facade or roofing), the total area of openings on each face represents 30% or more of the total area of the face, the rules defined in 7.3 and 7.4 of EC 1 (insulated roofs) must be applied.
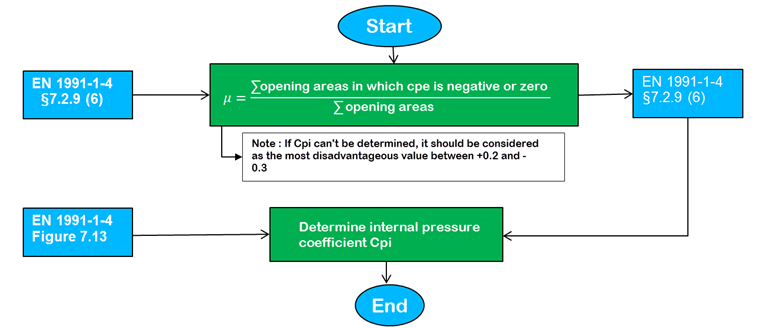
The internal pressure coefficient can be determined in a few steps (see Image 01).
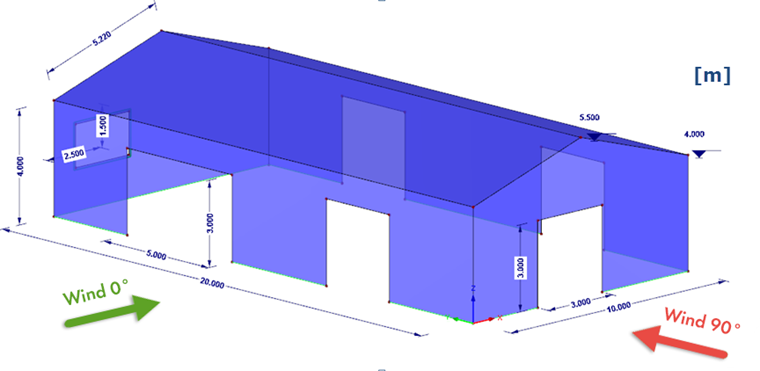
Practical Case: Open Industrial Hangar
Dimensions:
Openings
Determining Percentage of Opening Areas of Each Face
| Face Area | Area of Openings | Percentage | |
|---|---|---|---|
| Long pan 0° | 80 m2 | 24.00 m2 | 30% |
| Long pan 180° | 80 m2 | 18.00 m2 | 23% |
| Pinion-90° | 47.5 m2 | 9.00 m2 | 19% |
| Pinion + 90° | 47.5 m2 | 3.75 m2 | 7.9% |
| 0° slope | 104.4 m2 | 0.00 m2 | 0% |
| 180° slope | 104.4 m2 | 0.00 m2 | 0% |
When examining the areas of the openings, no face has more than 30% open area. Thus, we are in the presence of a building without a dominant face.
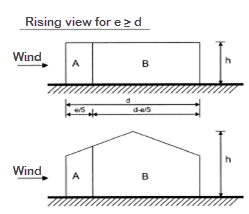
Calculation of Width e
Conclusion: When e ≥ d (depth of the building is d = 10 m), there is no C zone.
Calculation of h/d
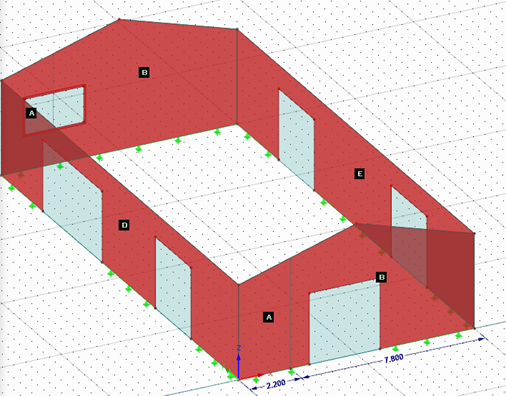
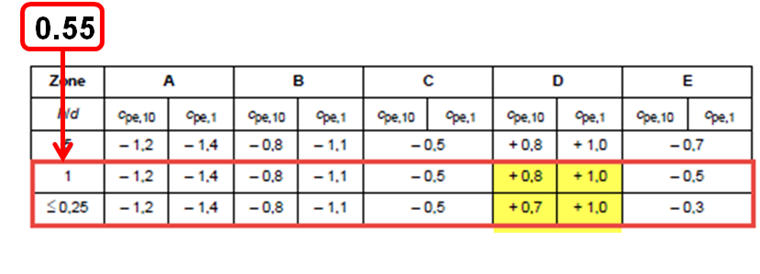
Reading Zones
where cpe is negative.
Opening Report
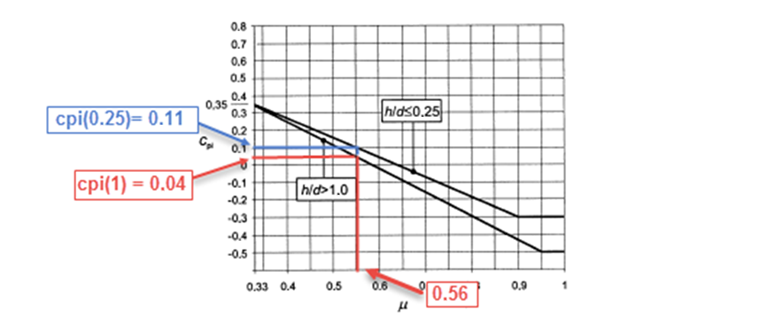
Reading Coefficient cpi
- If cpi is read on the corresponding curve for each wind and opening configuration.
- If cpi is obtained by linear interpolation between the two curves for each configuration.
Interpolation for Determining cpi
For buildings with a dominant face, meaning a building with one face of which the area is twice the size of all the other areas:
- cpi = 0.75 ⋅ cpe if the opening areas of the dominant face are twice the size of the other openings
- cpi = 0.9 ⋅ cpe if the opening areas of the dominant face are three times the size of the other openings
In most cases (for common buildings), without precise knowledge of the distribution of the openings, the standard recommends using extreme values cpi = +0.2 (overpressure) and cpi = 0.3 (underpressure).
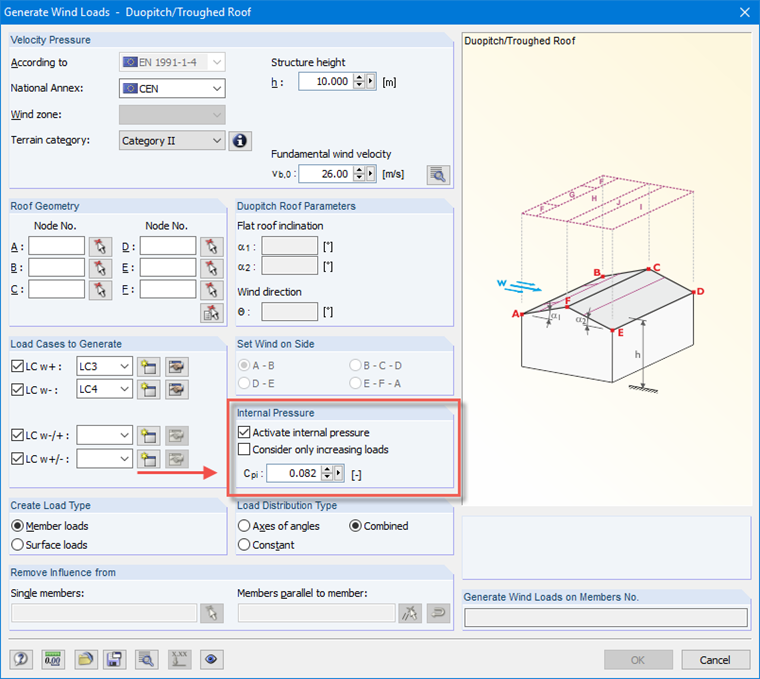
Consideration of Internal Pressure Coefficient in RFEM
In RFEM's wind load generators, the value of the internal pressure coefficient can be entered after it has been determined. These data are then considered during the automatic creation of the loads.