In order to combine the snow loads with other actions (imposed loads, wind, and so on) in defined design situations according to the combination standard DIN EN 1990, the load is classified accordingly as variable, fixed, and static action [1], [2]. The conditions present at the corresponding place of construction (normal or exceptional) are important. A normal condition is assumed if exceptional snowfall is unlikely to happen at this location.
In this case, the load for the persistent/transient design situation has to be determined. An exceptional condition is assumed if snowfall is likely to happen at this location. In the North German Plain, snow loads up to a multiple of the numerical values have been recorded in rare cases. In this case, the load for the persistent/transient and accidental design situation has to be determined. According to the National Annex, drifted snow loads are not accidental actions.
| [3] | Normal Conditions | Exceptional Conditions |
|---|---|---|
| Case | Case A – DIN EN 1991-1-3 3.2(1) | B1 – DIN EN 1991-1-3 3.3(1) |
| Description | No accidental snowfall / No accidental drifted snow load | Accidental snowfall / No accidental drifted snow load |
| Design Situation 1 | Persistent/transient | Persistent/transient |
| Snow load s on the roof – non-drifted | ||
| Snow load s on the roof – drifted | ||
| Design Situation 2 | - | Accidental (if snow is the accidental action) |
| Snow load s on the roof – non-drifted | - | where |
| Snow load s on the roof – drifted | - | where |
where
| μi | Roof snow load shape coefficient |
| Ce | Exposure coefficient (Ce = 1.0 shall be applied according to NA) |
| Ct | Temperature coefficient (Ct = 1.0 shall be applied according to NA) |
| sk | Characteristic Value of Snow Load on Ground |
| sAd | Design value for accidental snow loads on the ground |
| Cesl | Coefficient for exceptional snow loads (according to [5], Cesl = 2.3 in the North German Lowlands) |
Characteristic Value of Snow Load on Ground
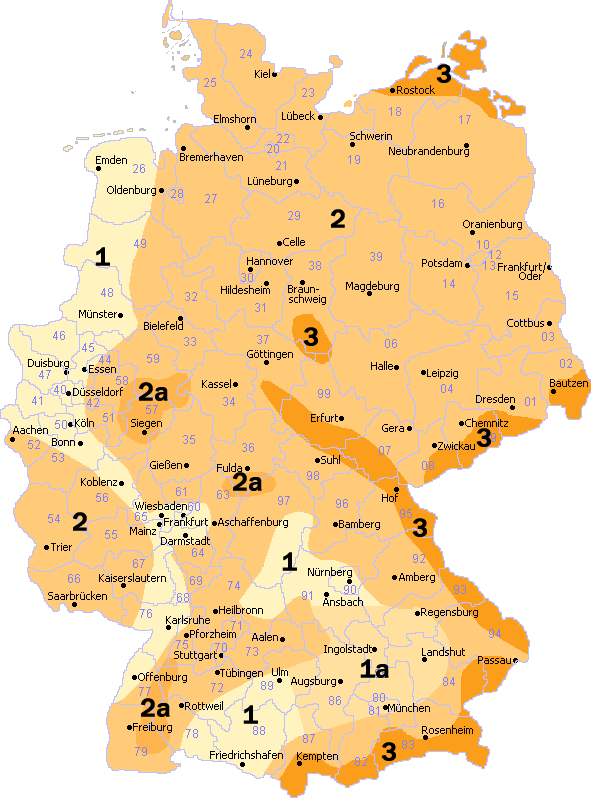
"The characteristic value of snow load on the ground is a fractile value of 98% with an annual probability exceedance value of 0.02 and a return period of 50 years." [3] This value is defined in the National Annex of Germany and is calculated depending on the snow load zone and the height above sea level. The National Annex [2] shows a map of Germany with zone indications in Figure NA.1. The exact assignment of snow loads of administrative units, particularly at the edges of the zones, has to be checked with the competent authorities [5]. The German Center of Competence for Construction (DIBt) offers (in German) the table "Categorization of snow load zones according to administrative limits" for each land area on this subject on its website. Moreover, this table indicates, for each administrative area, the assignment to the North German Plain concerning the implementation of the accidental design situation.
| Zone [2],[4] | Characteristic value of the snow load sk on the ground in kN/m² |
|---|---|
| 1 | |
| 1a | |
| 2 | |
| 2a | |
| 31) | |
| 3a and > 3a2) | |
| A | Ground elevation above sea level in m |
| 1) | In Zone 3, higher values may govern than according to the equation mentioned above for certain locations (for example, Oberharz, high altitudes of Fichtelgebirge, Reit im Winkl, Obernach/Walchensee). Information on the snow load in these regions has to be requested from the competent authorities. |
| 2) | New zones 3a and> 3a on the basis of [4] according to the notification of the Supreme Building Authority in the Bavarian State Ministry of the Interior of January 19, 2018. |
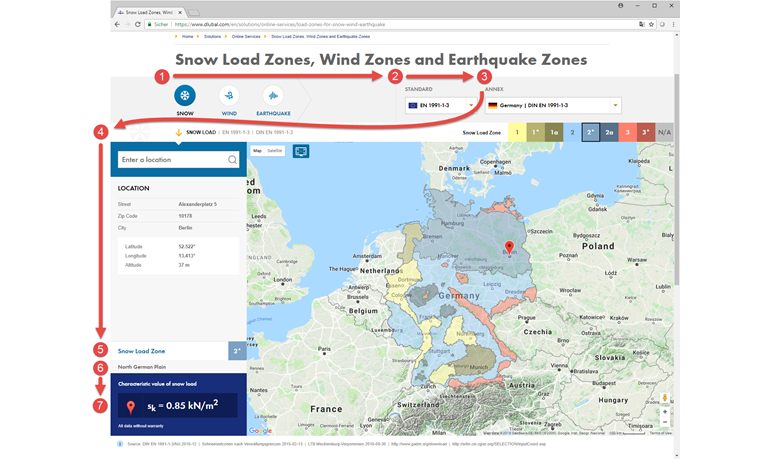
Determination with Dlubal Online Service
The Dlubal online service Snow Load, Wind Speed, and Seismic Zone Maps combines the standard specifications with digital technologies.
The service places the respective zone map over the Google Maps map, depending on the selected load type (snow, wind, earthquake) and the country-specific standard. Enter the location, geographic coordinates, or local conditions in the search function to get the relevant data. The tool then determines the characteristic load or acceleration at this location by means of the exact height above sea level and the zone data entered. If it is impossible to define the location by means of a specific address, you can zoom into the map and select the correct location. When selecting the correct location on the map, the calculation will be adapted to the new altitude and will display the updated loads.
The online service is available on the Dlubal website at Solutions → Online Services.
By specifying the parameters (1-4), you obtain the following (5-7) for the selected location:
- Load type = snow
- Standard = EN 1991-1-3
- Annex = Germany | DIN EN 1991-1-3
- Address = Zellweg 2, Tiefenbach
- Snow load zone
- Additional information, if applicable
- Characteristic value of the snow load sk
If you select a location in the North German Plain, the online service displays the message "North German Plain" at step 6. Then, the calculated load has to be considered as exceptional snow action in the exceptional design situation.
Shape Coefficient of Selected Roofs
Snow can occur in many different load distributions on a roof [1]. Among other things, the snow load depends on the shape of the roof, the insulating properties, the surface roughness, the heat buildup under the roof, the neighboring buildings, the surrounding area, and of course, the local climate. Hence, it is essential that a non-drifted and a drifted distribution of the snow load is considered during the design. The snow load to be applied acts perpendicularly and refers to the horizontal projection of the roof surface.
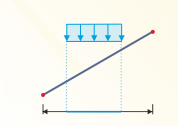
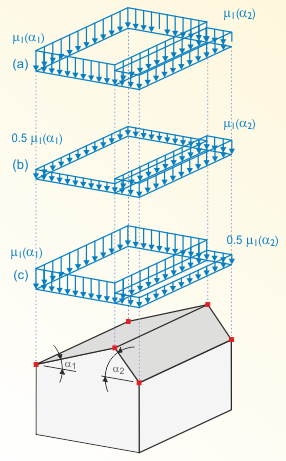
Basically, the shape factor μi depends on the inclination α of the considered roof surface.
| Shape Factor | Roof Inclination in α | ||
|---|---|---|---|
| μi | |||
| μi(α) | 0.8 | 0 |
Note: The shape coefficients apply if the snow can slide off the roof without being obstructed. If the sliding is obstructed (for example, by a snow guard, attic, and so on), shape coefficient 0.8 has to be applied.
A uniformly distributed load has to be applied with and without drift for flat and monopitch roofs.
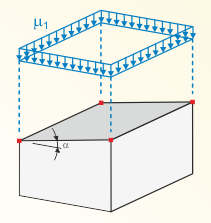
Three load arrangements have to be analyzed for duopitch roofs. Case a) shows the distribution without wind effects. Cases b) and c) show the distribution with influences from drift and melting. These two additional distributions often govern for structures that are sensitive to unequally distributed loads.