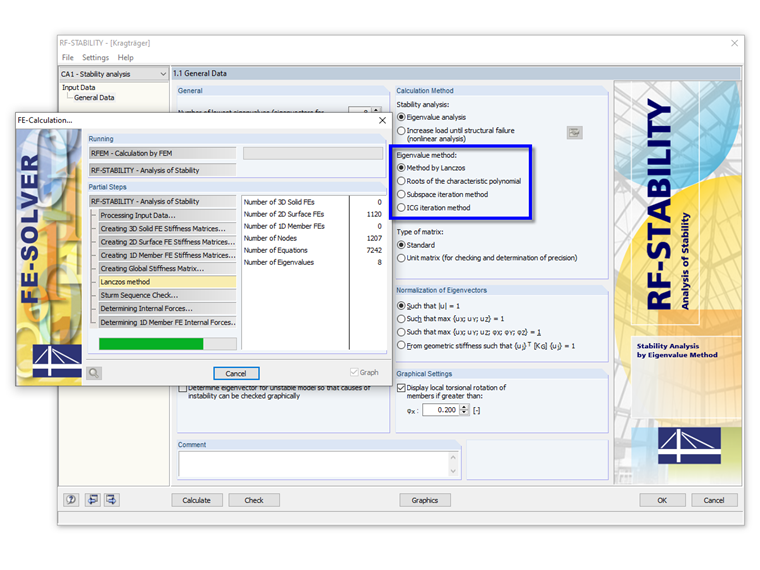
Método de Lanczos
Los valores propios se determinan directamente. Usando este algoritmo, generalmente se puede lograr una convergencia rápida. Este método es adecuado para modelos estándar y, por lo tanto, se establece de forma predeterminada.
Más información: método de Lanczos
Raíces del polinomio característico
Este método también se basa en un método de cálculo directo. Para grandes sistemas estructurales, este método puede ser más rápido que el método de Lanczos. La principal ventaja es la precisión del cálculo de valores propios más altos.
Más información: Polinomio característico
método de iteración del subespacio
Todos los valores propios se determinan en un solo paso. El espectro de la matriz de rigidez tiene una fuerte influencia en la duración del cálculo. Dado que la matriz de rigidez se almacena en la memoria operativa, este método no es adecuado para sistemas complejos. Además, se pueden mostrar factores de carga crítica negativos.
Más información: Método del subespacio de Krylov
método de iteración ICG
El método del gradiente conjugado incompleto requiere poca memoria de acceso aleatorio. Dado que los valores propios se determinan uno tras otro, esto requiere más tiempo de cálculo para el cálculo de sistemas estructurales pequeños y medianos, en comparación con el método directo. Sin embargo, el espectro no influye en la duración del cálculo. El método ICG es adecuado para análisis de sistemas muy grandes con pocos valores propios. Este método no proporciona ningún factor de carga crítica negativo.
Más información: Método del CG