Obecné
Při posouzení průřezů se vychází z vnitřních sil, které se obvykle počítají pro zatížení, jejich působiště je známé a pevně dané. Při posouzení jeřábových drah nebo mostů pozemních komunikací je ovšem třeba zohlednit také pohyblivá provozní zatížení. Působiště těchto zatížení jsou proměnná v čase.
Pro posouzení nosné konstrukce je třeba znát maximální a minimální vnitřní síly a reakce. Pro nalezení rozhodujících působišť zatížení můžeme použít příčinkové čáry.
Výpočet příčinkových čar
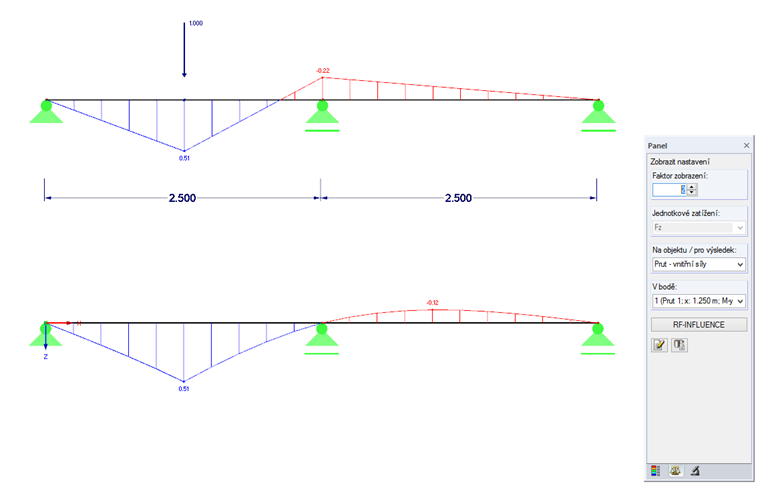
Stejně jako u nepohyblivého zatížení se jako základní krok vytvoří řez, na kterém se mají vypočítat vnitřní síly. Uvažuje se přitom jednotkové zatížení, jehož působiště je proměnné. Obrázek 01 ukazuje srovnání vyhodnocení vnitřní síly My pro nepohyblivé zatížení Fz s x = 1,25 m a příčinkové čáry ηMy pro pohyblivé jednotkové zatížení Fz = 1 a vyhodnocovací polohu x = 1,25 m.
Pro určení příčinkové čáry necháme osamělé břemeno posunovat se přes danou nosnou konstrukci a pro každé jednotlivé místo zaznamenáme vliv na posuzovaný řez jako pořadnici η. Pořadnice přitom mohou být kladné i záporné. Pokud má pořadnice hodnotu η = 0, přetíná v daném místě příčinková čára základní čáru. Zatížení v tomto místě tak nemá žádný vliv na sledovanou vnitřní sílu. Na obr. 01 se jedná o případ, kdy se zatížení nachází přímo nad podporou.
Jestliže spojíme všechny koncové body stanovených pořadnic, dostaneme příčinkovou čáru.
Vyhodnocení příčinkových čar
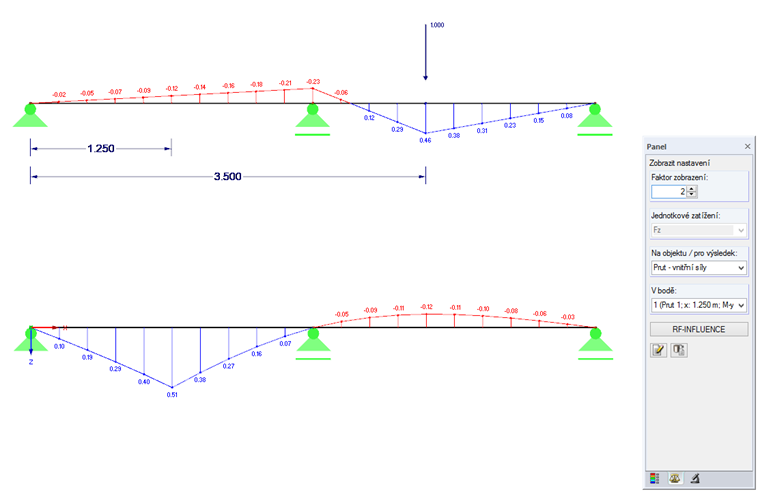
Na obr. 02 jsme na horní nosník o dvou polích umístili staticky působící zatížení do bodu x = 3,50 m. Na dolním nosníku o dvou polích je vyhodnocena příčinková čára pro místo x = 1,25 m. Nyní bychom měli vysvětlit význam pojmu „vliv“. V místě x = 1,25 m vzniká moment My = -0,12 kNm, pokud je zatížení Fz = 1,0 kN v x = 3,50 m.
Při zohlednění příčinkové čáry ηMy se nachází x x 3,50 m pořadnice η = -0,12.
Závěr: Libovolné zatížení Fz, které leží v x = 3,50 m, vyvolá moment My = -0,12 ⋅ Fz v x = 1,25 m. (Hodnota -0,12 je zaokrouhlena. Přesná hodnota je -0,11507.)
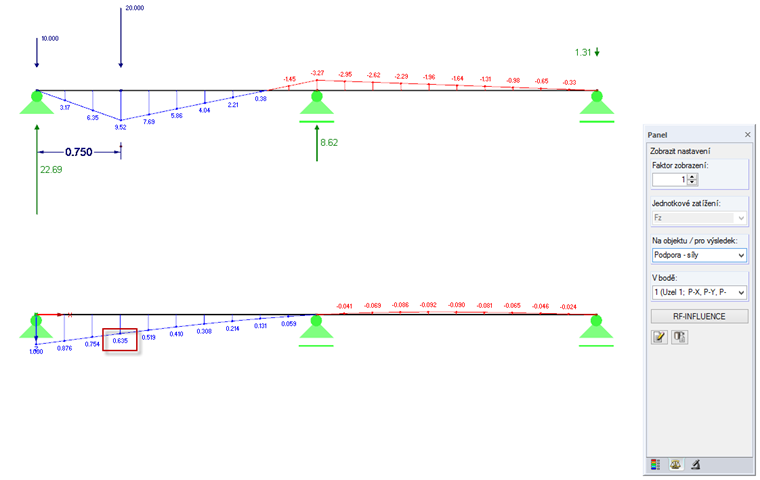
Na dalším jednoduchém příkladu, který je znázorněn na obr. 03, si popíšeme vyhodnocení příčinkové čáry pro reakci v levé podpoře při působení pohyblivé soustavy dvou osamělých břemen. Jednotkové zatížení Fz = 1 vyvolává v podpoře sílu 1,0 kN. Pořadnice η je tak 1,0. Libovolné zatížení P tedy vyvolává v podpoře sílu P ⋅ η. Pokud je k dispozici více zatížení, každé zatížení Pi vyvolává v podpoře sílu Pi ⋅ ηi.
Podporovou sílu tak vypočítáme následovně:
Příklad z obr. 03:
Pro výpočet maximálního zatížení podpory je třeba soustavu břemen umístit do kladné oblasti příčinkové čáry. Pro stanovení minima se soustava břemen musí naopak nacházet v její záporné oblasti.
Obecně platí: Pokud chceme nalézt extrémní hodnotu, musíme největší zatížení umístit přímo nad vrchol příčinkové čáry. Užitečné je přitom grafické znázornění příčinkové čáry v modulu RF-INFLUENCE.
Závěr
Příčinkové čáry používáme pro nalezení extrémních hodnot podporových reakcí a vnitřních sil v případě pohyblivých zatížení.
Z průběhu příčinkové čáry můžeme určit rozhodující zatížení, a nalézt tak na posuzovaném řezu pro příslušnou vnitřní sílu mezní hodnotu.
Příčinková čára se sice zobrazí po celé délce zkoumaného konstrukčního prvku, všechny uvedené pořadnice η ovšem vypovídají o vlivu na určitou veličinu na jediném místě nosníku.
Přídavný modul RF-INFLUENCE je nástroj, který slouží ke stanovení příčinkových čar u prutů a příčinkových ploch u plošných prvků pro vnitřní síly, reakce a deformace.