Ogólne informacje
Sprawdzenia przekrojów dokonuje się na siłach wewnętrznych, które w większości przypadków określa się dla obciążeń o znanym punkcie przyłożenia. Jednak przy projektowaniu belek podsuwnicowych lub mostów drogowych, pojawiają się również obciążenia ruchome. Punkty przyłożenia takich obciążeń są zmienne w czasie.
Do zaprojektowania konstrukcji wsporczej, muszą być znane maksymalne i minimalne siły wewnętrzne oraz reakcje podporowe. Do znalezienia głównych położeń obciążenia można wykorzystać linie wpływu.
Definiowanie linii wpływu
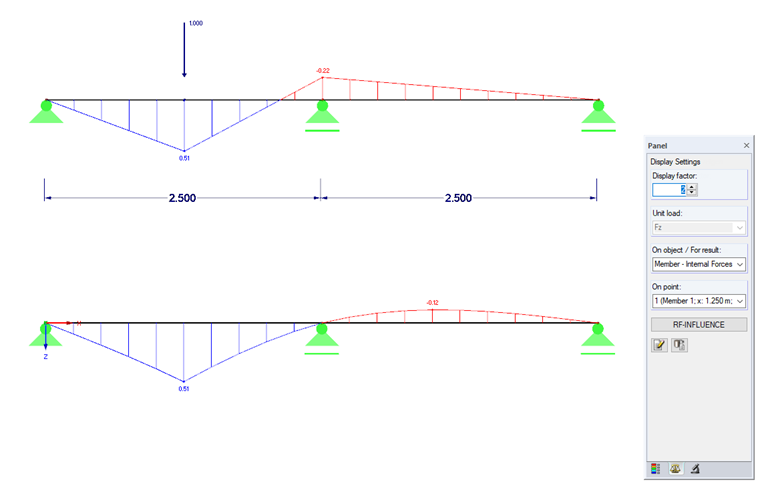
Podobnie jak w przypadku obciążenia statycznego, podstawą jest odnalezienie przekroju, dla którego określone zostaną ekstremalne siły wewnętrzne. Obciążenie jest realizowane poprzez obciążenie jednostkowe, którego lokalizacja jest zmienna. Rysunek 01 przedstawia porównanie analizy siły wewnętrznej My dla nieruchomego obciążenia Fz przy x = 1,25 m oraz linii wpływu ηMy dla ruchomego obciążenia jednostkowego Fz = 1 z pozycją analizy x = 1,25 m.
Aby wyznaczyć linię wpływu, na konstrukcję nośną i dla każdego położenia obciążenia „przetacza się“ pojedyncze obciążenie; wpływ na analizowany przekrój jest zapisywany jako rzędna η. Wartości η mogą być dodatnie lub ujemne. Jeżeli w danym punkcie η = 0, punkt ten jest nazywany punktem oddzielenia obciążenia. W tym miejscu zmienia się znak wartości wyniku. Tym samym, obciążenie przyłożone w tym miejscu nie ma wpływu na badaną siłę wewnętrzną. Na Rysunku 01 punkt oddzielenia obciążenia znajduje się bezpośrednio nad podporą.
Jeżeli wszystkie obliczone wartości wpływu dla określonych współrzędnych zostaną ze sobą połączone, zostaje utworzona linia wpływu.
Ocena linii wpływu
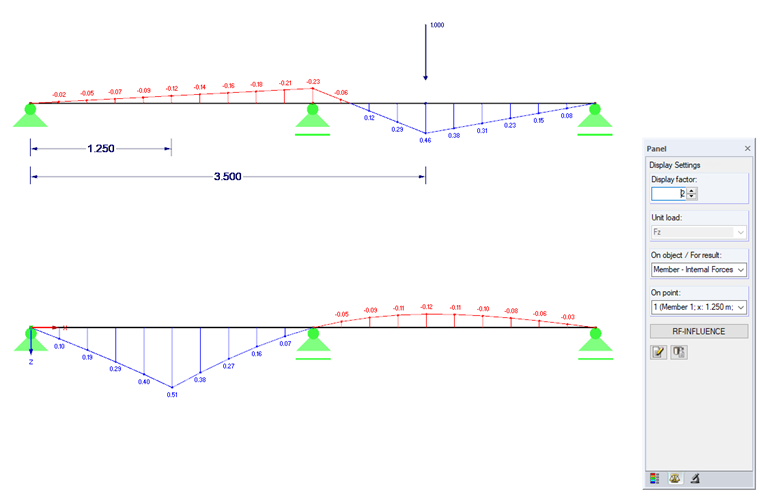
Na Rysunku 02 przyłożone zostało działające obciążenie konstrukcyjne w x = 3.50m co przedstawione zostało na pierwszej belce dwuprzęsłowej. Linia wpływu została przedstawiona na drugiej belce dwuprzęsłowej i jest ponownie oceniana dla x = 1.25 m. Tutaj należy wyjaśnić termin “wpływ”. W miejscu x = 1,25 m, prowadzi to do chwili mr = -0,12 kNm pod warunkiem, że masa Mz = 1,0 kN x = 3,50 m.
Jeżeli uwzględniona zostanie teraz linia wpływu ηMy , rzędna η = -0,12 znajduje się w odległości x = 3,50 m.
Posumowanie: Każde obciążenie Fz, które znajduje się w punkcie x = 3,50 m, generuje moment My = -0,12 ⋅ Fz przy x = 1,25 m. (Wartość -0.12 jest zaokrąglona. Wartość -0.12 jest zaokrąglona.)
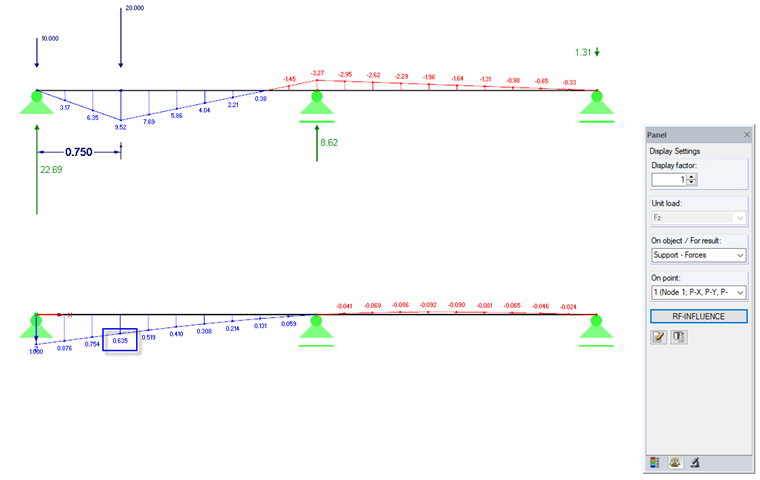
Kolejny prosty przykład przedstawiony na Rysunku 03 pokazuje ocenę linii wpływu dla reakcji podporowej w podporze znajdującej się z lewej strony, dla obciążenia parą sił skupionych. Obciążenie jednostkowe Fz = 1 generuje w podporach siłę 1,0 kN. Wartość η wynosi tym samym 1.0. Dlatego każde obciążenie P generuje siłę P ⋅ η w podporze. Jeżeli dostępnych jest kilka obciążeń, każde pojedyncze obciążenie Pi generuje siłę Pi ⋅ ηi w podporze.
Siła podporowa daje wynik:
Przykład z Rysunku 03:
Aby zdefiniować maksymalną reakcję podporową, obciążenie zestawem sił należy zastosować w obszarze o dodatniej wartości linii wpływu. Jeżeli ma zostać zdefiniowane obciążenie minimalne, wówczas obciążenie parą sił należy zastosować w obszarze o ujemnej wartości linii wpływu.
Ogólna zasada: Aby znaleźć wartość ekstremalną, większe obciążenie zostaje umieszczone bezpośrednio nad wartością ekstremalną linii wpływu. W tym przypadku przydatne jest graficzne wyświetlanie linii wpływu w module RF-INFLUENCE.
Wniosek
Linie wpływu są stosowane do odnajdowania wartości ekstremalnych reakcji podporowych i sił wewnętrznych powstałych od obciążeń ruchomych.
Kształt linii wpływu umożliwia wysnucie wniosku na temat lokalizacji obciążenia, potrzebnego do odnalezienia wartości granicznej odpowiedniej siły wewnętrznej ocenianego przekroju.
Linia wpływu jest wyświetlana na całej długości elementu konstrukcyjnego objętego oceną, ale wszystkie wskazane wartości η opisują wpływ na konstrukcję tylko w jednym, analizowanym miejscu belki.
Moduł RF-INFLUENCE jest narzędziem do definiowania linii wpływu dla prętów i powierzchni, służącym do określenia sił wewnętrznych, reakcji podporowych i odkształceń.