Součinitel citlivosti θ
Součinitel citlivosti θ je definován následovně [1]:
| θ | Součinitel citlivosti mezipatrového posunu |
| Pcelk | Celkové tíhové zatížení na podlaží a nad ním uvažované v seizmické návrhové situaci |
| dr | návrhový posun mezi podlažími stanovený jako rozdíl průměrných bočních posunůds v horní a dolní části příslušného podlaží; v tomto případě se posuny stanoví pomocí lineárního spektra návrhové odezvy s q = 1,0 |
| Vcelk | Celkový seizmický smyk podlaží stanovený pomocí lineárního návrhového spektra odezvy |
| h | Výška poschodí |
Pokud je 0,1 < θ ≤ 0,2, lze účinky druhého řádu zohlednit přibližně součinitelem 1 / (1 − θ).
Pro θ > 0,2 je třeba při výpočtu vlastních čísel a multimodální analýze spektra odezvy zohlednit geometrickou matici tuhosti.
Součinitel citlivosti lze vypočítat také v programech RFEM 6 a RSTAB 9. Další informace najdete v tomto článku databáze znalostí: KB | Stanovení součinitele citlivosti pro posouzení nutnosti teorie druhého řádu pro dynamickou analýzu .
Geometrická matice tuhosti
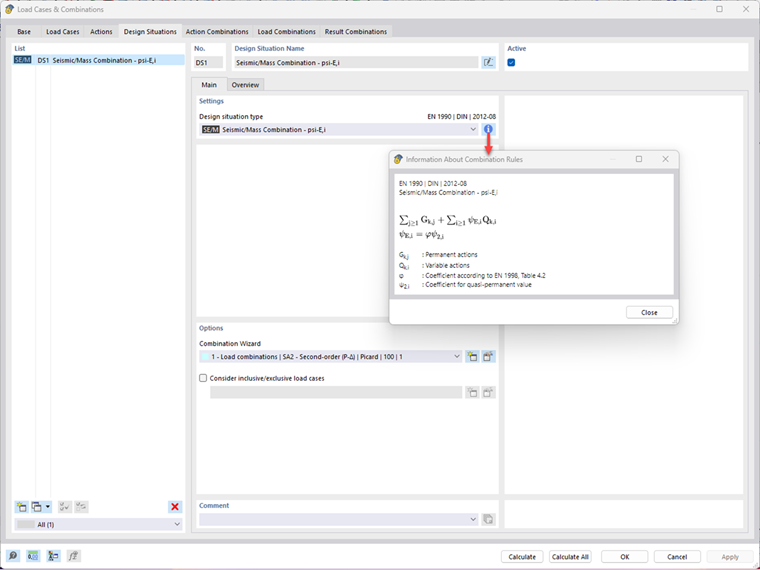
Pro dynamickou analýzu se iterační výpočty pro stanovení nelineárních účinků druhého řádu nehodí. Problém lze linearizovat a pro zohlednění účinků druhého řádu stačí použít geometrickou matici tuhosti z osových zatížení. Přitom se vychází z toho, že se svislá zatížení vlivem vodorovných účinků nemění a deformace jsou malé ve srovnání s rozměry budovy [2]. Uvažovaná zatížení by měla odpovídat zatížením pro seizmické návrhové situace podle EN 1990, odstavec 6.4.3.4 [3]:
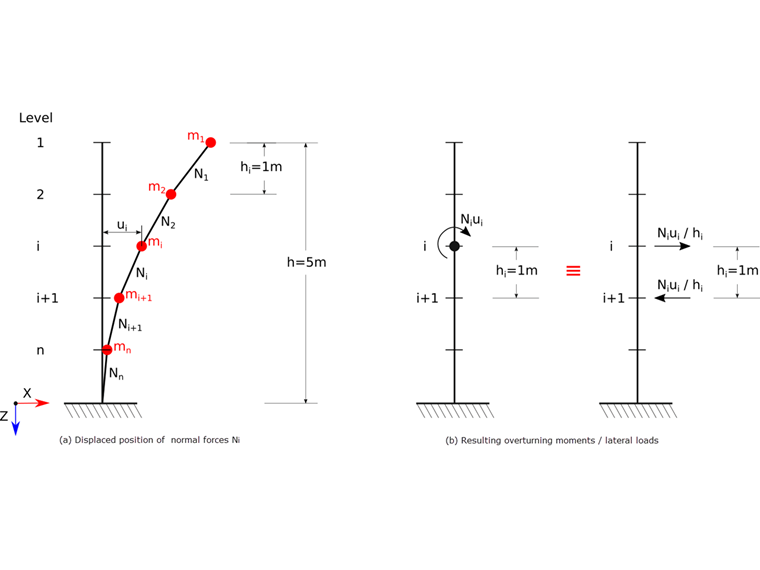
Normálové tahové síly zvyšují tuhost, jako například u předpjatého lana. Tlakové síly snižují tuhost a mohou vést k singularitám v matici tuhosti. Geometrická tuhost Kg není závislá na mechanických vlastnostech systému, ale pouze na délce prutu L a normálové síle N v něm. Pro ilustraci základního problému použijeme jednoduchý příklad konzoly znázorněné na obrázku 1. Jednotlivé hmotné body konzoly představují jednotlivá podlaží budovy. Budova je podrobena dynamické analýze se zohledněním účinků druhého řádu. Normálové síly Ni na jednotlivých podlažích i = 1...n vycházejí ze svislých sil v seizmické návrhové situaci. Výška podlaží je definována prostřednictvím hi.
Geometrickou matici tuhosti Kg lze odvodit z podmínek statické rovnováhy:
Pro jednoduchost zde uvádíme pouze stupně volnosti vodorovných posunů. Uvedené odvození je založeno na použití klopícího momentu v důsledku účinku lineárního posunu. Jedná se o zjednodušení pro ohybový prvek a přesný předpoklad pro příhradový prvek. Přesnější stanovení geometrické matice tuhosti pro ohybové nosníky lze provést pomocí metody kubického posunu nebo pomocí analytického řešení diferenciální rovnice ohybové čáry. Podrobnější informace a odvození naleznete ve Werkle [4]. Geometrická matice tuhosti Kg se přičte k matici tuhosti systému K a získá se upravená matice tuhosti Kmod:
Kmod = K + Kg
V případě tlakových normálových sil tak dochází ke snížení tuhosti.
Příklad: Vlastní frekvence a multimodální analýza spektra odezvy se zohledněním účinků druhého řádu
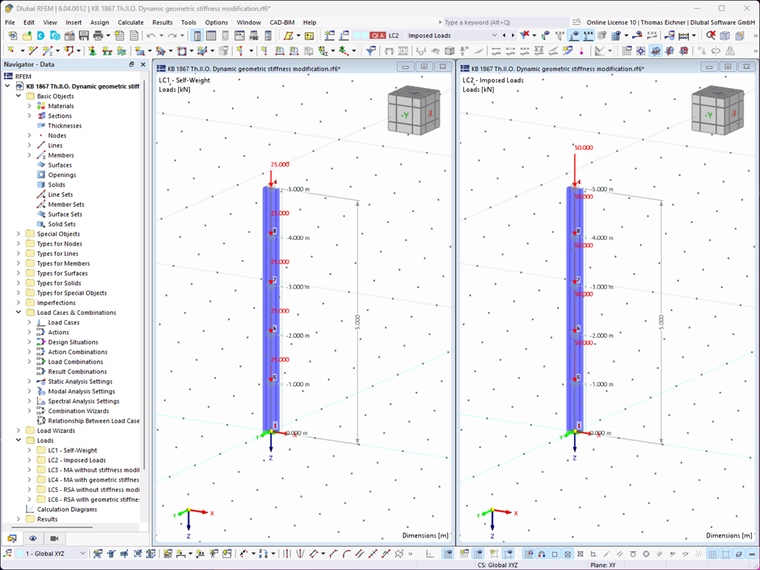
Dále vám ukážeme, jak lze zohlednit geometrickou matici tuhosti v programech RFEM 6 a RSTAB 9. Jako příklad použijeme konzolu znázorněnou na obrázku 1. Konzola se skládá z pěti hmotných bodů. V globálním směru X přitom vždy působí 4 000 kg.
Průřez je IPE 300 z materiálu S 235 s Iy = 8 356 ∙ 10-5 m4 a E = 2,1 ∙ 1011 N/m2. Aby bylo možné zohlednit geometrickou matici tuhosti v dynamické analýze, vytvoříme v hlavním programu RFEM návrhovou situaci typu Seizmická/hmotová kombinace. Následně používaná kombinace zatížení (KZ1) se automaticky vytvoří pomocí kombinatoriky integrované v programu.
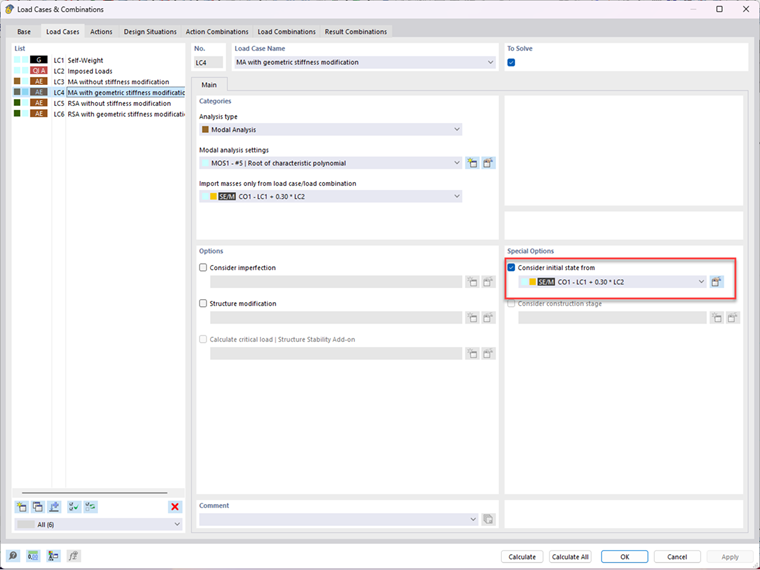
Addon Modální analýza umožňuje stanovit vlastní tvary a účinné modální hmoty konstrukce. Přitom lze definovat počáteční stavy pro zohlednění změn tuhosti na základě zatěžovacích stavů a kombinací zatížení.
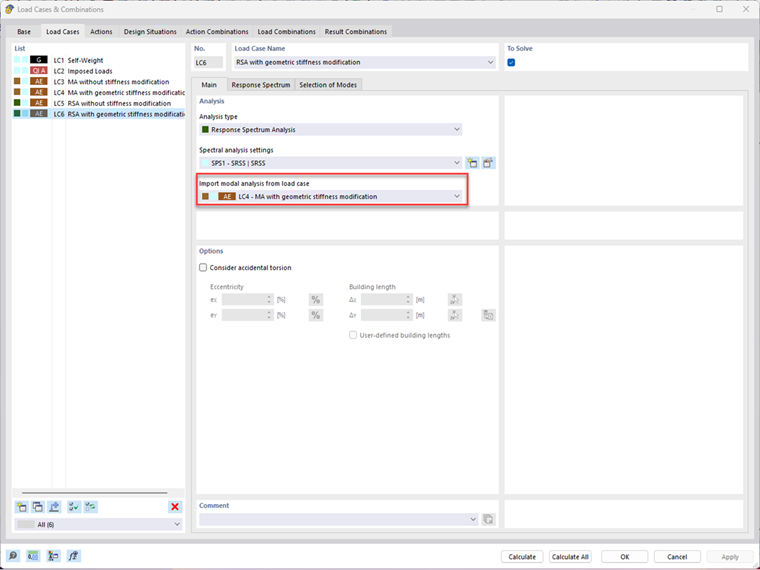
Zadáme dva zatěžovací stavy pro modální analýzu. Do ZS4 se importuje ZS1 pro zohlednění geometrické matice tuhosti a tím i účinků druhého řádu. Pro srovnání je definován ZS3, který neobsahuje žádné změny tuhosti.
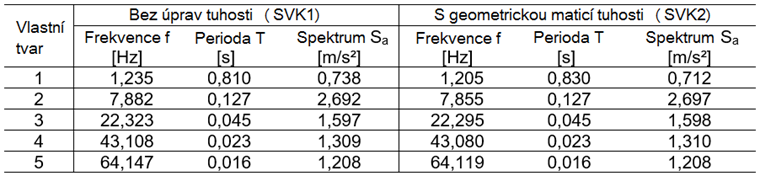
V následující tabulce jsou uvedeny vypočítané vlastní frekvence f [Hz], vlastní periody T [sec] a hodnoty zrychlení Sa [m/s2] ze spektra odezvy bez a s geometrickou maticí tuhosti Kg z normálových sil z KZ1.
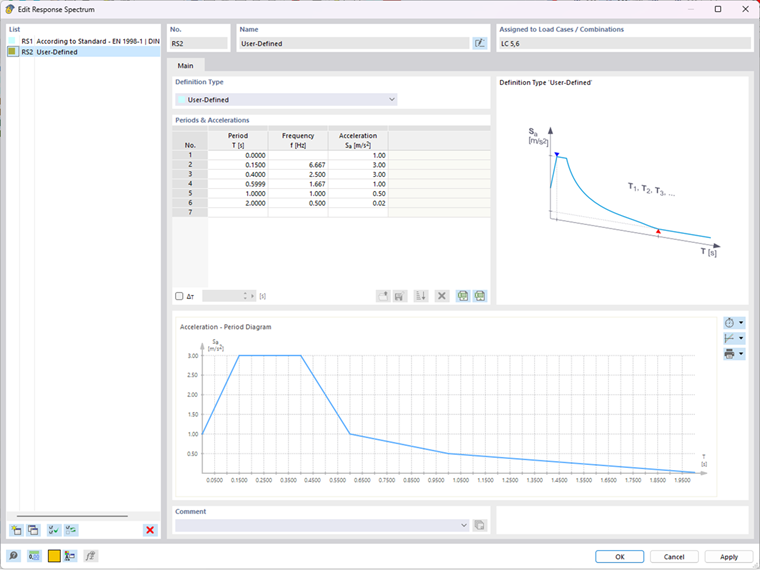
Při multimodální analýze spektra odezvy se s pomocí vlastních frekvencí stanoví hodnoty zrychlení z definovaného spektra odezvy. Na základě těchto hodnot zrychlení program stanoví vnitřní síly spektra odezvy. Grafické znázornění uživatelsky definovaného spektra odezvy je znázorněno na obrázek 6 a hodnoty zrychlení Sa [m/s2] stanovené ze spektra odezvy pro každé vlastní číslo jsou uvedeny v tabulce výše.
Aby bylo zajištěno správné přiřazení upravených frekvencí, je třeba při vytváření zatěžovacího stavu spektra odezvy vycházet z požadované modální analýzy.
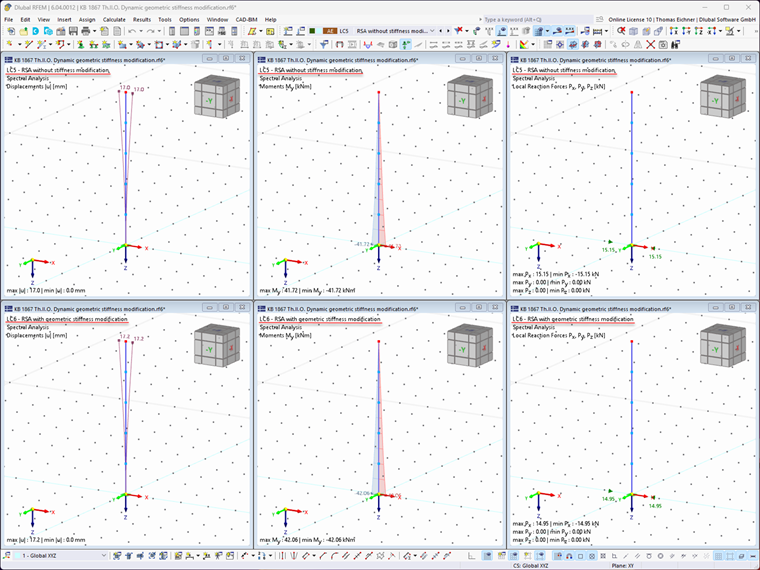
V případě tlakových normálových sil vede zohlednění geometrické matice tuhosti ke snížení vlastní frekvence a může vést k nižším hodnotám zrychlení Sa, jako v našem příkladu. Samotná úprava vlastních frekvencí není dostatečná pro zohlednění účinků druhého řádu; to může vést i k nižším výsledkům, a nebýt tak na straně bezpečnosti. Upravenou matici tuhosti je velmi důležité použít také pro stanovení vnitřních sil a deformací. Při analýze spektra odezvy se upravená tuhost z modální analýzy automaticky použije pro stanovení výsledků analýzy spektra odezvy. Deformace, vnitřní síly a podporové reakce stanovené analýzou spektra odezvy s maticí geometrické tuhosti a bez ní jsou znázorněny na obrázku 8.
Zohlednění geometrické matice tuhosti vede k větším deformacím a vnitřním silám. Při zohlednění geometrické matice tuhosti jsou ovšem výsledná zatížení na podporách o něco menší.