Back to FAQ
1717x
003547
Sonja von Bloh, M.Sc.
2021-06-14

Effective Element Thickness and Small Shear Area Calculation in SHAPE-THIN

SHAPE‑THIN calculates a very small shear area. What is the cause?

Answer:

The shear area is calculated as follows:

Ay = Iz2∫A*Szt*2dA*

Iz

Second moment of area in relation to the axis z or y

Sz

First moment of area in relation to the axis z

t*

Effective element thickness for the shear transfer

A*

Surface area based on the effective shear thickness t*
Shear Area Ay

Az = Iy2∫A*Syt*2dA*

Iy

Second moment of area in relation to the axis y

Sy

First moment of area related to the axis y

t*

Effective element thickness for the shear transfer

A*

Surface area based on the effective shear thickness t*
Shear Area Az

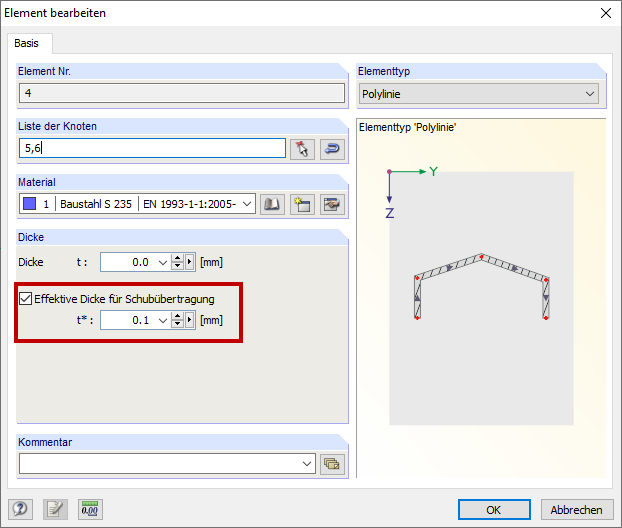
The effective element thickness for the shear transfer t* has a significant influence on the shear area. Therefore, the defined effective element thickness for the shear transfer t* (Image 01) of the elements should be checked.

FAQ|003547
EN-US | Flag FAQ
[EN] FAQ 003547 | SHAPE‑THIN calculates a very small shear area. Why?
Effective Shear Thickness t*
Effective Shear Thickness t*
Author

Ms. von Bloh provides technical support for our customers and is responsible for the development of the SHAPE‑THIN program as well as steel and aluminum structures.

Downloads
SHAPE-THIN Model File
268 KB
;