The shear correction factor is considered in the RF‑LAMINATE add-on module using the following equation.
The calculation of shear stiffness can be found in the English version of the RF‑LAMINATE manual, page 15 ff.
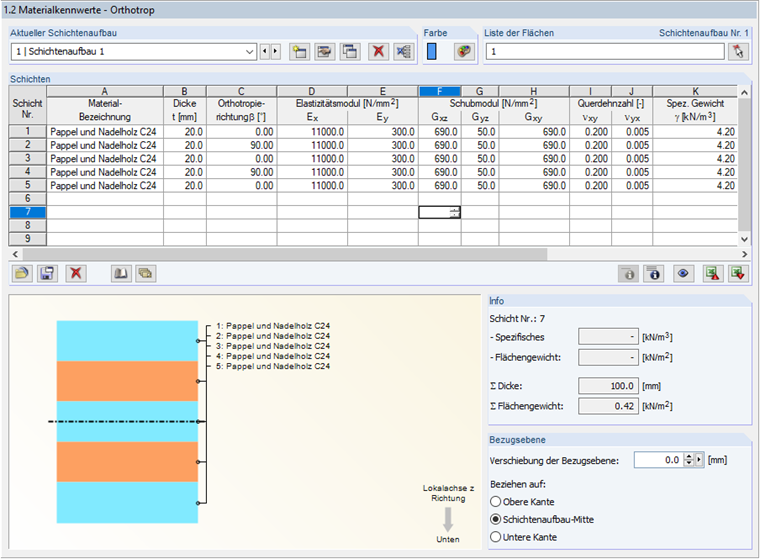
For a plate with the thickness of 10 cm in Image 01, the calculation of the shear correction factor is shown. The equations used here are only valid for simplified symmetrical plate structures!
| Layer | zmin | zmax | Ex(z)(N/mm²) | Gxz(z)(N/mm²) |
|---|---|---|---|---|
| 1 | -50 | -30 | 110000 | 690 |
| 2 | -30 | -10 | 300 | 50 |
| 3 | -10 | 10 | 110000 | 690 |
| 4 | 10 | 30 | 300 | 50 |
| 5 | 30 | 50 | 110000 | 690 |
| χ1 | 13.75 · 106 |
| χ2 | 8.935 · 106 |
| χ3 | 9.47 · 106 |
| χ4 | 8.935 · 106 |
| χ5 | 13.75 · 106 |
8.4642 · 1011
3.147 · 1013
2.5 · 1012
3.147 · 1013
8.4642 · 1011
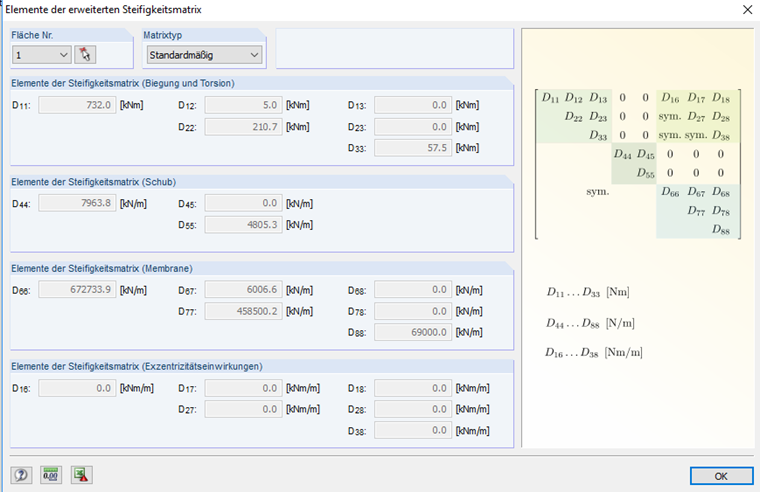
Total is 6.7133 · 1013
This corresponds to the resulting value in RF‑LAMINATE (Image 02).