Hardening Parameters in Nonlinear Material Models

Stress-Strain Diagram for Steel (Source: [1])

Theoretical Background

Strain hardening is characterized by internal variables. This is described in more detail in [2], for example. Using the internal variables, it is possible to consider damage or plasticity of materials, for example. The inner variables describe the dissipative effects of the material.

Hardening in RFEM (von Mises, Tresca, Drucker-Prager, Mohr-Coloumb)

According to [1], Sec. 4.4.2, the state functions of the internal variables, which are usually not observable, are used to describe material defects (displacements, microscopic cracks, and so on); they can be scalar (for example, isotropic damage) or tensorial (for example, kinematic hardening). To determine the internal variables, there are evolution equations (usually common differential equations) depending on the constitutive (independent and dependent) variables and the internal variables.

Equation 1:

These must be integrated with regard to the initial conditions. (Source: [1], Sec. 4.4.2)

Therefore, the internal variables are also referred to as a material memory with the initial condition at time t0.

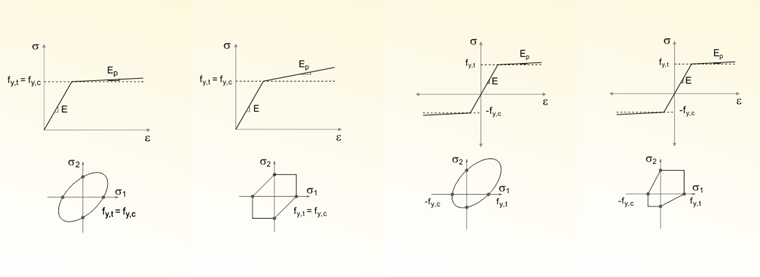
Isotropic hardening is "widening" of the yield surface without changing the surface position in the stress space. One example of this is a steel plate that expands in all directions, at least conceptually, due to hole bearing. After the plastic deformation, the isotropic material is still isotropic, at least in theory. Generally, isotropic hardening is described by the internal variable α.

Kinematic hardening refers to a translation (displacement) of the yield surface in the stress space. The yield surface does not change its shape. The kinematic hardening compensates the local internal stresses of the material, resulting from local displacement of the material. This is also referred to as the Bauschinger effect in the literature. In this case, the yield strength is reduced, as in the case of a wire bent in multiple places. Less and less force has to be applied to the bent wire the more often it is bent. In the case of kinematic hardening, the material is changed from isotropic to anisotropic. Generally, the kinematic hardening is described by the internal variable β.

• Free energy:
  $$\mathrm{\psi }: = \mathrm{\psi }({\mathrm{\epsilon }}^{\mathrm{e}},\mathrm{\alpha },\mathrm{\beta })$$

  Formula 15
• Dissipation of energy:
  $${\mathrm{D}}^{\mathrm{in}} = \mathrm{\sigma } · {\dot{\tilde{\mathrm{\epsilon }}}}^{\mathrm{p}} - \frac{\partial \mathrm{\psi }}{\partial \mathrm{\alpha }} · \dot{\mathrm{\alpha }} - \frac{\partial \mathrm{\psi }}{\partial \mathrm{\beta }} · \dot{\mathrm{\beta }}$$

  Formula 16
• Thermodynamic forces: Isotropic:
  $$\mathrm{\alpha } = - \frac{\partial \mathrm{\psi }}{\partial \mathrm{\alpha }}$$

  Formula 17
• Thermodynamic forces: Kinematic:
  $$\mathrm{\tau } = - \frac{\partial \mathrm{\psi }}{\partial \mathrm{\beta }}$$

  Formula 18

Equation 2:

Equation 3:

Equation 4:

In Equation 4, σe = F(σij) is the "effective" stress of the material in the spatial state of stress. On the other hand, K is the limit stress in the uniaxial compression-tension test.

This is based on the assumption that plastic material behavior in the multiaxial stress state corresponds to the uniaxial state (idealization).

In the case of kinematic hardening, the tensor αij describes the center of the yield surface. The center is shifted by the respective load step dα ij (see Figure 03).

The displacement of the yield surface is quite complicated to take into account in a program due to the material displacement that takes place analogously. Currently, this hardening type is not taken into account in RFEM.

One possible approach is the displacement according to the Prager rule with c as a material constant:

The effective plastic strain is decomposed into kinematic and isotropic hardening.

Equation 5:

Equation 6:

Equation 7:

m is a factor for checking the ratio of isotropic to kinematic hardening.

a) Isotropic, b) Kinematic, c) Mixed Hardening (Source: [3])

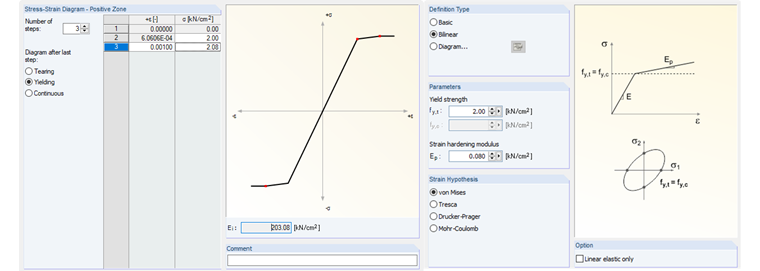
Definition of Strain Hardening in RFEM

As mentioned in the previous article about the Damage material model, user-defined strain hardening is required in the program once you select the "Diagram" option.

• KB 001461 │ Nonlinear Material Model Damage

For this, the 3rd step is defined in Image 04, which considers the strain hardening of the material according to von Mises during the plastification.

Equation 8:

Equation 9:

Stress-Strain Diagram (Manual)

The example shown in Image 04 uses a material with a hardening factor of m = Ep = 0.08 kN/cm² and an elastic modulus of concrete E = 3,100 kN/cm². The stress in Step 2 and Step 3 of the model is changed as follows.

Equation 10:

Equation 11:

Equation 12:

Equation 13:

This example shows how you can consider the strain hardening of isotropic plastic material behavior in the diagram of the Damage material model. For the second strain step, a very large strain step of ε2 = 1 is defined, which is close to ∞.

Conclusion

A user-defined definition of stress-strain diagrams is always required when defining special materials. In the case of such materials, it is also useful to define a strain hardening in order to achieve a better convergence and more realistic consideration of the material behavior.

By defining intermediate points, it is also possible to consider isotropic hardening by entering the "Diagram", even for nonlinear materials.