Principes théoriques
L'écrouissage est caractérisé par des variables internes. Cette opération est décrite plus en détail dans [2]. Les variables internes permettent par exemple de considérer l'endommagement ou la plasticité des matériaux. Les variables internes décrivent les effets dissipatifs du matériau.
Selon [1], section 4.4.2, les fonctions d'état des variables internes, qui ne sont généralement pas visibles, sont utilisées pour décrire les défauts de matériau (déplacements, fissures mineures, etc.) ; elles peuvent être scalaires (par exemple, endommagement isotrope) ou tendues (par exemple, durcissement cinématique). Pour déterminer les variables internes, il existe des équations d'évolution (généralement des équations différentielles courantes) dépendantes des variables de comportement (indépendantes et dépendantes) et des variables internes.
Équation 1 :
Celles-ci doivent être intégrées en fonction des conditions initiales. (Source : [1], section 4.4.2)
Par conséquent, les variables internes sont également appelées mémoire de matériau avec la condition initiale à l'instant t0.
Le durcissement isotrope « élargi » la surface d'élasticité sans modifier la position de la surface dans l'espace de contrainte. Un exemple de ce comportement est celui d'une plaque d'acier qui s'élargit - au moins presque - en raison de la contrainte d'appui dans toutes les directions. Après la déformation plastique, le matériau isotrope est toujours isotrope, du moins en théorie. En général, le durcissement isotrope est décrit par la variable interne α.
Le durcissement cinématique fait référence à une translation (déplacement) de la surface d'élasticité dans l'espace des contraintes. La surface d'élasticité ne change pas de forme. Le durcissement cinématique compense les contraintes internes locales du matériau, résultant d'un déplacement local du matériau. Elle est également appelée « effet Bauscher » dans la littérature spécialisée. Dans ce cas, la limite d'élasticité est réduite, comme dans le cas d'un fil plié en plusieurs points. D'une part, le fil courbe doit absorber les efforts les plus faibles. Dans le cas d'un durcissement cinématique, le matériau passe d'isotrope à anisotrope. En général, le durcissement cinématique est décrit par la variable interne β.
- Énergie libre :
- Dissipation de l'énergie :
- Forces thermodynamiques : Isotrope :
- Forces thermodynamiques : Cinématique :
Équation 2 :
Équation 3 :
Équation 4 :
Dans l'Équation 4, σe = F(σij) est la contrainte « efficace » du matériau dans l'état spatial de contrainte. D'autre part, K est la contrainte limite dans l'essai uniaxial de traction-compression.
Ce résultat est basé sur l'hypothèse que le comportement plastique du matériau à l'état de contrainte multiaxiale correspond à l'état uniaxial (idéal).
Dans le cas du durcissement cinématique, le tenseur αij décrit le centre de la surface d'élasticité. Le centre est déplacé par le pas de charge correspondant dα ij (voir la Figure 03).
Le programme considère le déplacement de la surface d'élasticité dû au déplacement du matériau identique. Ce type de durcissement n'est actuellement pas pris en compte dans RFEM.
Une approche possible est le déplacement selon la règle de Prager avec c comme constante de matériau :
La déformation plastique efficace est décomposée en écrouissement cinématique et isotrope.
Équation 5 :
Équation 6 :
Équation 7 :
m est un facteur pour vérifier le rapport entre le durcissement isotrope et cinématique.
Définition du durcissement dans RFEM
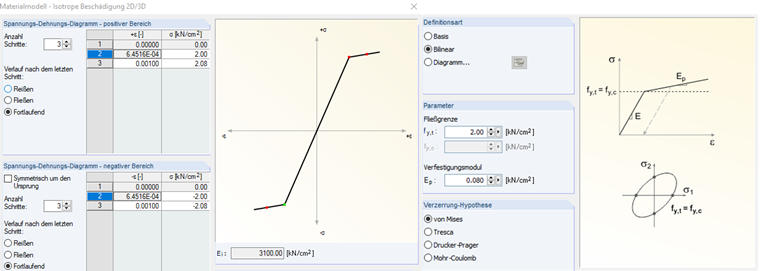
Comme mentionné dans mon article précédent sur le modèle de matériau Endommagement, un écrouissage défini par l'utilisateur est requis dans le programme dès que vous sélectionnez l'option « Diagramme ».
Pour ce faire, le 3e est définie sur la Figure 04, qui considère le durcissement du matériau selon von Mises pendant la plastification.
Équation 8 :
Équation 9:
L'exemple de la Figure 04 utilise un matériau avec un facteur de durcissement de m = Ep = 0,08 kN/cm² et un module d'élasticité du béton E = 3 100 kN/cm². La contrainte aux étapes 2 et 3 du modèle est modifiée comme suit.
Équation 10:
Équation 11:
Équation 12:
Équation 13:
Cet exemple explique comment considérer le durcissement du comportement de matériau plastique isotrope dans le diagramme du modèle de matériau Endommagement. Pour le deuxième pas de déformation, un très grand pas de déformation ε2 = 1 est défini, ce qui est proche de ∞.
Conclusion
Une définition personnalisée des diagrammes de contrainte-déformation est toujours requise lors de la définition des matériaux spéciaux. Dans le cas de tels matériaux, il est également utile de définir un durcissement afin d'obtenir une meilleure convergence et une considération plus réaliste du comportement du matériau.
La définition des points intermédiaires permet également de considérer le durcissement isotrope en entrant le « Diagramme », même pour les matériaux non linéaires.
![Diagramme de contrainte-déformation pour l'acier (source: [1])](/fr/webimage/009400/466787/01-de.png)
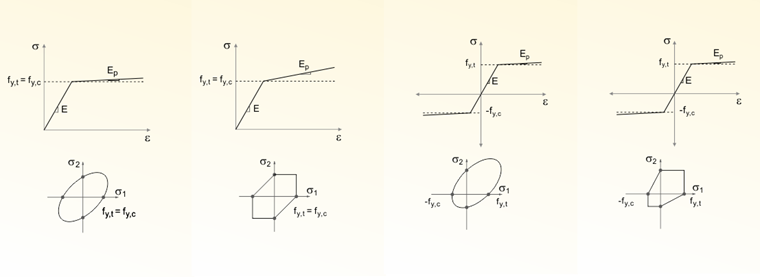
![a) Isotrope, b) Cinématique, c) Durcissement mixte (Source: [3])](/fr/webimage/009402/466791/03-de.png)