Teoretické pozadí
Zpevnění se popisuje pomocí vnitřních proměnných, což je detailněji popsáno např. v [2]. Prostřednictvím vnitřních proměnných lze zohlednit např. poškození nebo plasticitu materiálu. Vnitřní proměnné popisují disipativní účinky materiálu.
Podle [1], kap. 4.4.2 se stavové veličiny vnitřních proměnných, které obecně nelze pozorovat, používají při popisu defektů materiálu (sedání, mikrotrhliny atd.). Může se jednat o skaláry (např. izotropní poškození) nebo o tenzorické veličiny (např. kinematické zpevnění). Vnitřní proměnné se určují vývojovými rovnicemi (lze říci, že se jedná o běžné diferenciální rovnice) v závislosti na konstitutivních (nezávislých a závislých) proměnných a samotných vnitřních proměnných,
Rovnice 1:
které je nutné zaintegrovat se zohledněním počátečních podmínek (zdroj: [1], kap. 4.4.2).
Vnitřní proměnné se tudíž označují také jako paměť materiálu s počáteční podmínkou v časovém bodě t0.
Izotropní zpevnění je "rozšíření" plochy plasticity beze změny polohy plochy v napěťovém prostoru. Jako příklad může posloužit ocelový plech, který se přinejmenším teoreticky může otlačováním natahovat všemi směry. Izotropní materiál je po plastické deformaci přinejmenším teoreticky i nadále izotropní. Izotropní zpevnění lze obecně popsat pomocí vnitřní proměnné α.
Kinematické zpevnění označuje posun (posun) plochy plasticity v napěťovém prostoru. Plocha plasticity svůj tvar nemění. Kinematické zpevnění se rovná vlastním lokálním napětím materiálu, které jsou výsledkem jeho lokálního posunu. Tento jev bývá v literatuře popisován jako Bauschingerův efekt. Hranice plasticity se zde snižuje stejně jako v případě drátu, který je opakovaně ohýbán. Čím častěji se drát ohýbá, tím méně síly je k jeho ohýbání zapotřebí. Při kinematickém zpevnění se materiál přeměňuje z izotropního na anizotropní. Kinematické zpevnění se obecně vyjadřuje prostřednictvím vnitřní proměnné β.
- Volná energie:
- Rozptyl energie:
- Termodynamické síly izotropně:
- Termodynamické síly kinematicky:
Rovnice 2:
Rovnice 3:
Rovnice 4:
V rovnici 4 je σe = F (σij ) „účinné“ napětí materiálu v prostorové napjatosti. k je oproti tomu hraniční napětí v jednoosém testu tlak-tah.
Vychází se přitom z předpokladu, že plastické chování materiálu ve víceosém stavu napětí odpovídá jednoosému stavu (v ideálním případě).
V případě kinematického zpevnění popisuje αij střed plochy plasticity. Střed se posune dalším zatěžovacím krokem dαij (viz obr. 03).
Z důvodu analogicky probíhajícího posunu materiálu není snadné zohlednit posun plochy plasticity v programu. Momentálně tento druh zpevnění v programu RFEM zohledněn není.
Možným vyjádřením je posun podle Pragerova pravidla, kde c je konstanta materiálu:
Efektivní plastické přetvoření se rozloží do kinematického a izotropního zpevnění.
Rovnice 5:
Rovnice 6:
Rovnice 7:
m je faktor, prostřednictvím kterého lze sledovat poměr mezi izotropním a kinematickým zpevněním.
Definice zpevnění v programu RFEM
Po vybrání volby „Diagram“ program uživatele vyzve, aby sám zadal zpevnění, což je zmíněno v předchozím příspěvku o materiálovém modelu Poškození.
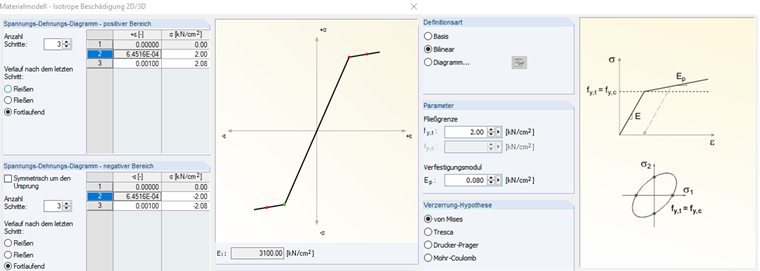
3 Na Obrázku 04 je definován krok, který zohledňuje deformační zpevnění materiálu podle von Misese během plastifikace.
Rovnice 8:
Rovnice 9:
Na příkladu znázorněném na ob. 04 je použit materiál s faktorem zpevnění m = Ep = 0,08 kN/cm² a modulem pružnosti betonu 3 100 kN/cm². Napětí v krocích 2 a 3 v modelu se mění následovně.
Rovnice 10:
Rovnice 11:
Rovnice 12:
Rovnice 13:
Tento příklad ukazuje, jakým způsobem může být zpevnění izotropně plastického chování materiálu zohledněno v diagramu. Pro druhý krok přetvoření je definován značně velký krok protažení ε2 = 1, který se blíží ∞.
Závěr a výhled
Pokud se jedná o speciální materiály, musí uživatel ručně zadat diagramy pro napětí a přetvoření. I v případě těchto materiálů má pro dosažení lepší konvergence a z důvodu realistického posouzení chování materiálu smysl definovat zpevnění.
Pomocí mezikroků zadaných uživatelem je i v případě nelineárních materiálů možné pomocí volby „Diagram“ zohlednit izotropní zpevnění.
![Pracovní diagram pro ocel (zdroj: [1])](/cs/webimage/009400/466787/01-de.png)
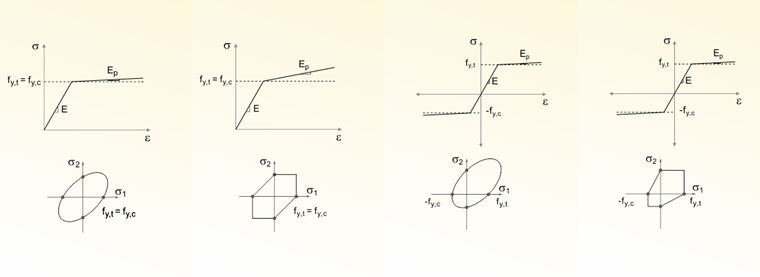
![a) izotropní, b) kinematické, c) smíšené zpevnění (zdroj: [3])](/cs/webimage/009402/466791/03-de.png)