Theoretischer Hintergrund
Verfestigung wird über innere Variablen beschrieben. Detaillierter ist dies zum Beispiel in [2] beschrieben. Über die inneren Variablen werden zum Beispiel Schädigung oder Plastizität von Materialien berücksichtigt. Die inneren Variablen beschreiben die dissipativen Effekte des Materials.
"Die im Allgemeinen nicht beobachtbaren Zustandsgrößen der inneren Variablen werden zur Beschreibung materieller Defekte (Versetzungen, Mikrorisse etc.) herangezogen, es können skalare (zum Beispiel isotrope Schädigung) oder tensorielle Größen (zum Beispiel kinematische Verfestigung) sein. Für die Bestimmung der inneren Variablenwerden Evolutionsgleichungen (im Allgemeinen gewöhnliche Differenzialgleichungen)in Abhängigkeit von den konstitutiven (unabhängigen und abhängigen) Variablen und inneren Variablen selbst angegeben,
Gleichung 1:
die unter Berücksichtigung der Anfangsbedingungen zu integrieren sind." (Quelle:[1], Kap. 4.4.2)
Die inneren Variablen werden deshalb auch als materielles Gedächtnis bezeichnet mit der Anfangsbedingung zum Zeitpunkt t0.
Isotrope Verfestigung bezeichnet das "Aufweiten" der Fließfläche, ohne dass sich die Lage der Fläche im Spannungsraum ändert. Ein Beispiel hierfür ist ein Stahlblech, was sich zumindest gedanklich durch Lochleibung in alle Richtungen aufweitet. Nach der plastischen Verformung ist ein isotroper Werkstoff zumindest theoretisch weiterhin isotrop. Im Allgemeinen wird die isotrope Verfestigung über die innere Variable α beschrieben.
Kinematische Verfestigung bezeichnet eine Translation (Verlagerung)der Fließfläche im Spannungsraum. Die Fließfläche ändert ihre Form nicht. Die kinematische Verfestigung gleicht den lokalen Eigenspannungen des Materials, welche aus lokalen Versetzungen des Materials resultieren. In der Literatur wird dies auch als Bauschinger-Effekt bezeichnet. Die Fließgrenze wird hier wie bei einem mehrfach gebogenen Draht herabgesetzt. Am gebogenen Draht muss immer weniger Kraft aufgewendet werden, je öfter er gebogen wird. Bei kinematischer Verfestigung wird das Material von isotrop in anisotrop geändert. Die Beschreibung der kinematischen Verfestigung erfolgt im Allgemeinen über die innere Variable β.
- Freie Energie:
- Dissipation der Energie:
- Thermodynamische Kräfte isotrop:
- Thermodynamische Kräfte kinematisch:
Gleichung 2:
Gleichung 3:
Gleichung 4:
In Gleichung 4 ist σe = F(σij) die "effektive" Spannung des Materials im räumlichen Spannungszustand. k hingegen ist die Grenzspannung im ein axialen Druck-, Zug-Test.
Dem liegt die Annahme zugrunde, dass plastisches Materialverhalten im mehraxialen Spannungszustand dem einaxialen Zustand entspricht (Idealisierung).
Bei kinematischer Verfestigung beschreibt der Tensor αij das Zentrum der Fließfläche. Das Zentrum wird durch den jeweiligen Lastschritt dαij verschoben (vergleiche Bild 03).
Das Verschieben der Fließfläche ist aufgrund der analog dazu erfolgenden Materialverschiebung recht umständlich in einem Programm zu berücksichtigen. Aktuell wird diese Art der Verfestigung in RFEM nicht berücksichtigt.
Ein möglicher Ansatz ist eine Verschiebung nach der Prager Regel mit c als Materialkonstante:
Die effektive plastische Dehnung wird in kinematische und isotrope Verfestigung zerlegt.
Gleichung 5:
Gleichung 6:
Gleichung 7:
m beschreibt hier einen Faktor, mit dem das Verhältnis von isotroper zu kinematischer Verfestigung kontrolliert wird.
Definition der Verfestigung in RFEM
Wie in einem vorigen Beitrag zum Materialmodel Schädigung erwähnt, ist eine benutzerdefinierte Verfestigung im Programm notwendig, sobald die Einstellung „Diagramm“ gewählt wird.
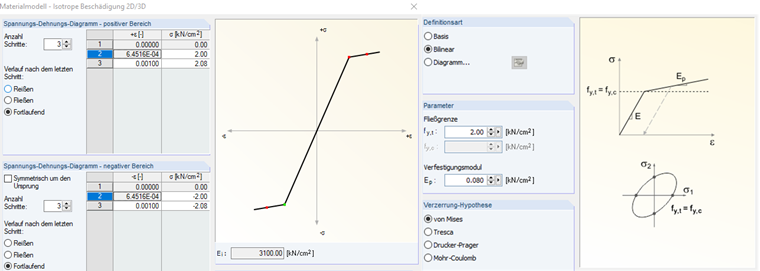
In Bild 04 ist hierzu als Beispiel ein 3. Schritt definiert worden, der die Verfestigung eines Materials nach von Mises während der Plastifizierung berücksichtigt.
Gleichung 8:
Gleichung 9:
Für das in Bild 04 dargestellte Beispiel wird ein Material mit einem Verfestigungsfaktor von m = Ep = 0,08 kN/cm² und einem E-Modul von Beton E = 3.100 kN/cm²verwendet. Die Spannung in den Schritten 2 und 3 des Modells wird hierzu wie folgt geändert.
Gleichung 10:
Gleichung 11:
Gleichung 12:
Gleichung 13:
Mit diesem Beispiel wird gezeigt, wie die Verfestigung von isotrop plastischem Materialverhalten im Diagramm des Materialmodels Schädigung berücksichtigt werden kann. Für den zweiten Dehnungsschritt wird mit ε2 = 1 ein sehr großer Dehnungsschritt definiert der nahe ∞ liegt.
Zusammenfassung
Die benutzerdefinierte Definition von Spannungs-Dehnungs-Diagrammen ist immer dann erforderlich, wenn spezielle Materialien definiert werden. Auch bei diesen Materialien ist es zur Erzielung einer besseren Konvergenz und zur realistischeren Berücksichtigung des Materialverhaltens sinnvoll, eine Verfestigung zu definieren.
Über benutzerdefinierte Zwischenpunkte ist es auch bei nichtlinearen Materialien über die Eingabe "Diagramm" möglich, isotrope Verfestigung zu berücksichtigen.
![Spannungs-Dehnungs-Diagramm Stahl (Quelle: [1])](/de/webimage/009400/466787/01-de.png)
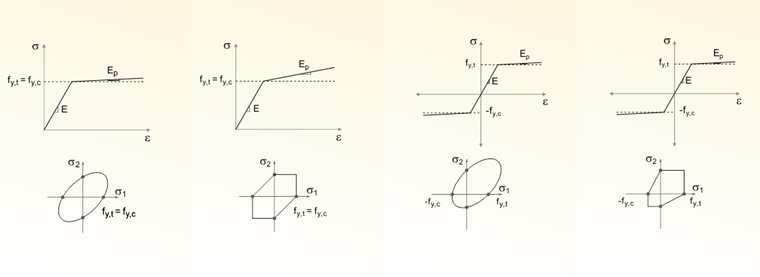
![a) isotrope, b) kinematische, c) gemischte Verfestigung (Quelle: [3])](/de/webimage/009402/466791/03-de.png)