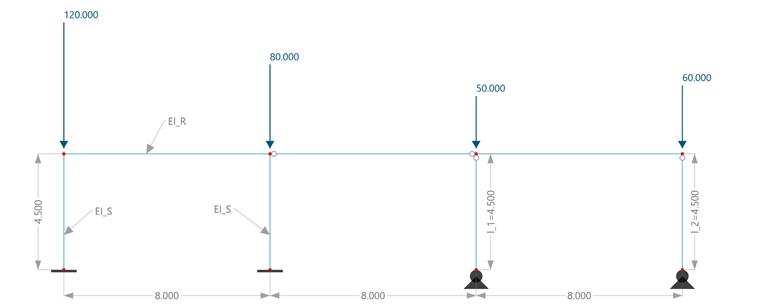
Descripción
Un pórtico coaccionado con dos pilares articulados adicionales está cargado con cargas puntuales verticales. Se debe calcular el factor de carga crítica determinante para el sistema estructural y se deben determinar las longitudes eficaces respectivas para los montantes del pórtico coaccionado.
Eingabeparameter y estructural System
| Parámetros del material | Módulo de elasticidad | E | 210000 | N/mm2 |
| Parámetro de la sección | Rigidez a flexión de los lados | E_IS | 8045,1 | kNcm2 |
| Rigidez a flexión de la viga | E_IR | 1825,53 | kNcm2 | |
| Geometría | luz del vano | l_R | 8.0 | m |
| Altitud | l=l1=l2 | 4.5 | m | |
| Hipótesis de carga | Montante 1 | N_le | 120 | kN |
| Montante 2 | Nri | 80 | kN | |
| Pilar articulado 1 | F1 | 50 | kN | |
| Pilar articulado 2 | F2 | 60 | kN |
Solución analítica
La solución analítica utiliza las fórmulas aproximadas según [1] para pórticos con zapatas coaccionadas.
El factor de carga crítica es mayor que 10, por lo que sería admisible el cálculo de los esfuerzos internos según el análisis estático lineal según EC 3-1-1.
Vergleich Solución analítica con RFEM-Lösung
| Valor de comparación | Solución analítica | RFEM 6 | Razón |
|---|---|---|---|
| f | 10,2524 | 10,085 | 1,017 |
| Lcr,le | 8,00 m | 8 m | 0,992 |
| Lcr,re | 10 m | 10 m | 0,992 |
Los resultados entre el cálculo manual y RFEM 6 se corresponden muy bien. Las desviaciones relativas son inferiores al 2%.
Referencias
[1] ALBERT, Andrej; ua: Tablas de construcción para ingenieros, con notas de cálculo y
ejemplos, 23 ed. Nördlingen