Requisitos de estabilidad
En sec. C1 [1], se enumeran cinco requisitos al considerar el cálculo de estabilidad de una estructura de acero. Directamente desde AISC 360-16, estos incluyen:
- Deformaciones de flexión, cortante y axiales de las barras, y todas las demás deformaciones de componentes y conexiones que contribuyen a los desplazamientos de la estructura
- Efectos de segundo orden (incluidos los efectos P-Δ y P-δ)
- Imperfecciones geométricas
- Reducciones de rigidez debidas a la inelasticidad, incluido el efecto de la fluencia parcial de la sección, que puede acentuarse por la presencia de tensiones residuales
- Incertidumbre en la resistencia y rigidez del sistema, barra y conexión
El método de cálculo de análisis directo se puede utilizar para cumplir con los requisitos anteriores. Este artículo se centrará principalmente en los puntos b al d y la aplicación en RFEM 6.
efectos de segundo orden
El análisis de la estructura considerará los efectos de segundo orden incluyendo P-Δ y P-δ. Cuando un elemento estructural como un pilar tiene una carga axial aplicada además de una carga lateral aplicada, el elemento se deformará. La distancia de flecha, Δ, multiplicada por la carga axial aplicada, P, crea un momento secundario denominado P-Δ que se debe considerar. Además, también se deben considerar en el análisis los efectos desestabilizadores de la carga axial que actúa a lo largo de la curvatura desviada de la barra, o P-δ. Fig. C-C2.1 [1] proporciona un ejemplo gráfico de estos efectos secundarios en una barra.
AISC enumera las condiciones en C2.1(b) [1] donde los efectos P-δ se pueden omitir por completo. De lo contrario, si una barra está sujeta tanto a compresión como a flexión, estas deformaciones localizadas se deben considerar en el análisis.
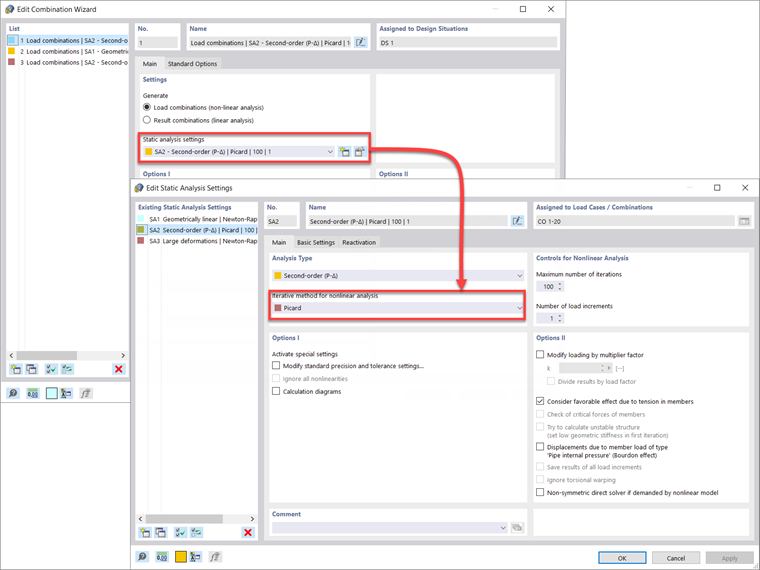
Dentro de RFEM 6, el análisis de segundo orden se resuelve iterativamente como una secuencia de problemas lineales donde el esfuerzo axil se actualiza desde la iteración anterior y se considera constante dentro del paso de iteración. Esta aproximación numérica es el método de iteración de punto fijo conocido como el método de Picard. Tanto los efectos secundarios P-Δ como P-δ se capturan automáticamente en las ecuaciones diferenciales subyacentes dentro del solucionador de RFEM 6 cuando se establece en este método.
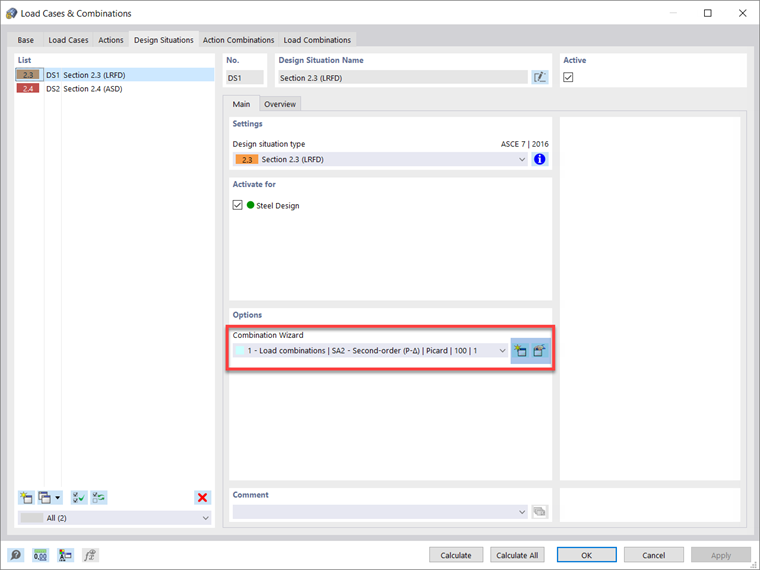
Las situaciones de proyecto y las combinaciones de carga en RFEM 6 se establecen de forma predeterminada en segundo orden y el método de Picard. El usuario puede modificar esta configuración predeterminada para las situaciones de proyecto LRFD o ASD, por ejemplo, en el Asistente para combinaciones - Configuración de análisis estático - Método iterativo para análisis no lineal.
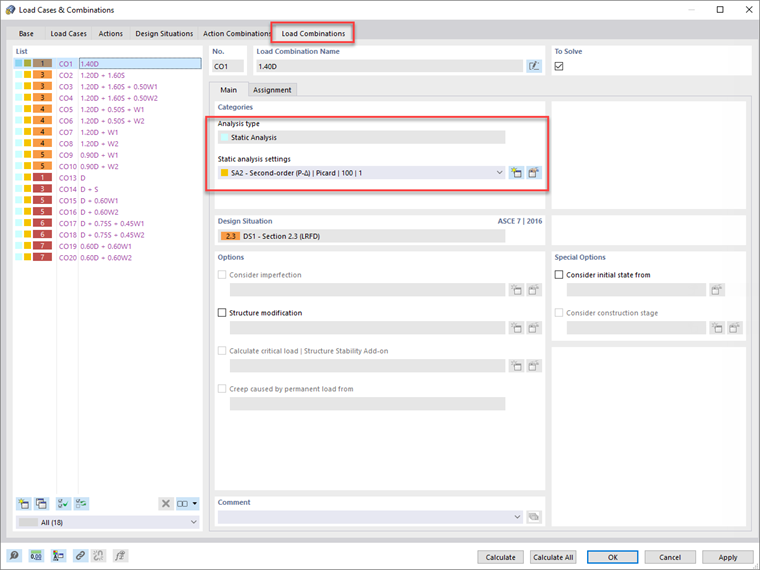
Las combinaciones de carga individuales seguirán posteriormente la configuración del análisis definida en la situación de proyecto respectiva. Sin embargo, el usuario puede modificar la configuración de la combinación de carga individualmente, si lo prefiere.
Para cumplir con la sección C2.1(b) [1], el usuario puede mantener el análisis de segundo orden predeterminado para la situación de proyecto 1 (LRFD) para el cálculo de la resistencia. Además, se puede establecer el tipo de análisis deseado para la Situación de proyecto 2 - ASD, que se puede usar para las comprobaciones de servicio junto con cualquier otra situación de proyecto creada. Visite el manual en línea de RFEM 6 Configuración del análisis estático para obtener más información sobre las opciones que se ofrecen dentro de estos cuadros de diálogo.
Imperfecciones geométricas
El apartado C2.2 [1] requiere que se consideren las imperfecciones de la estructura mediante el modelado directo de las imperfecciones o el uso de cargas ficticias. El AISC aclara aún más que la principal preocupación para las imperfecciones en las estructuras de edificios es la falta de plomada del pilar. En esta sección no se requiere la falta de rectitud de la barra, ya que este efecto se tiene en cuenta en el cap. E [1] para el cálculo a compresión.
El modelado directo de las imperfecciones debe considerar los desplazamientos iniciales debido a la carga y las formas del modo de pandeo anticipadas aplicadas para dar el mayor efecto desestabilizador. Dependiendo del tamaño de la estructura, esto podría llevar mucho tiempo y ser complicado. En su lugar, se puede utilizar el método alternativo con cargas teóricas aplicadas.
Según C2.2b(a) [1], las cargas ficticias se deben aplicar como cargas laterales aditivas en todos los niveles en todas las combinaciones de carga. La excepción dada en C2.2b(d) [1] incluye cuando la deriva de segundo orden de la estructura a la deriva de primer orden es igual o menor que 1,7; entonces las cargas teóricas se pueden aplicar a las combinaciones de carga solo de gravedad y excluirse de las combinaciones con otras cargas laterales aplicadas.
La magnitud de la carga teórica en cada nivel se puede calcular utilizando la ecuación C2-1 [1].
|
α |
= 1,0 (LRFD); 1,60 (ASD) |
|
Ni |
Carga ficticia aplicada en el nivel i, kips (N) |
|
Yi |
Carga de gravedad aplicada en el nivel i de la combinación de cargas LRFD o ASD, según corresponda, kips (N) |
Las cargas teóricas se deben aplicar en la dirección que cause el mayor efecto desestabilizador. Esto significa que para las combinaciones de carga solo de gravedad, las cargas teóricas se deben aplicar en ambas direcciones ortogonales. Para las combinaciones de carga con cargas laterales aplicadas, las cargas teóricas se deben aplicar en la misma dirección resultante de la carga lateral (por ejemplo, las cargas de viento en la dirección X deben incluir las cargas teóricas en la dirección X).
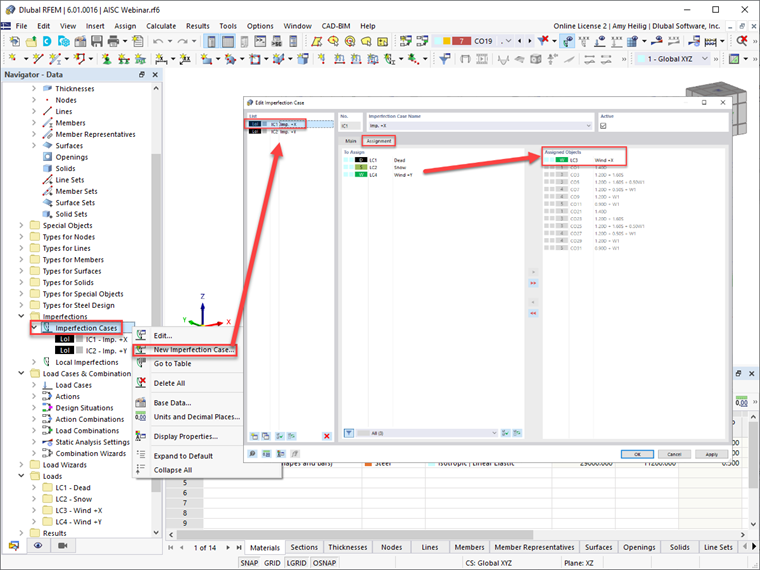
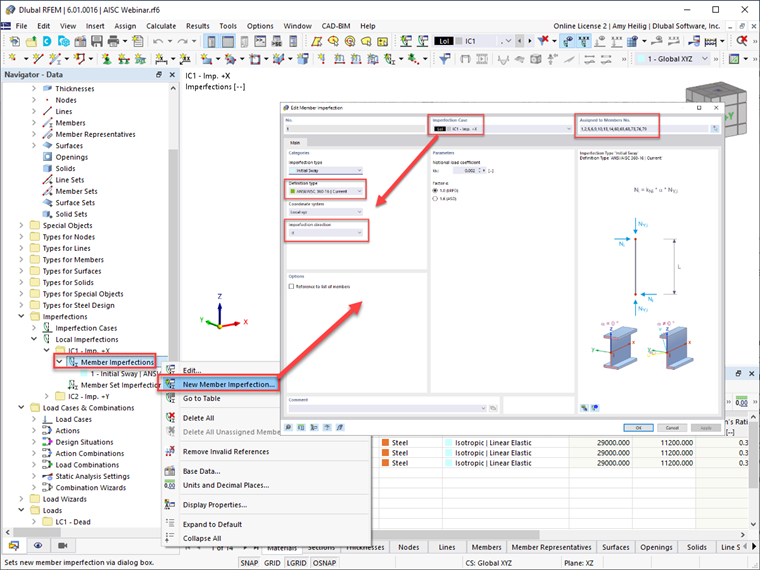
RFEM 6 ofrece a los usuarios la capacidad de definir casos de imperfección en las direcciones ortogonales, como en las direcciones ±X o ±Y. Los casos de carga se pueden asignar adicionalmente a cada caso de carga de imperfección, considerando el mayor efecto desestabilizador. RFEM asignará automáticamente el caso de imperfección a las combinaciones de carga generadas, como se muestra directamente en este cuadro de diálogo.
Una vez que se han definido los casos de imperfección, el usuario debe definir las imperfecciones de la barra en cada caso de imperfección. La norma "ANSI/AISC 360-16 | Actual" disponible en el menú desplegable considerará el esfuerzo axil de la barra de la combinación de carga asignada, utilice la ecuación C2-1 [1] y aplique la magnitud de la carga teórica calculada tanto al inicio como al final de la barra.
La norma "ANSI/AISC 360-16 | Carga gravitacional” permitirá al usuario referirse a una combinación de carga diferente a la actual para calcular el esfuerzo axil de la barra. También se debe especificar la dirección de la imperfección basada en los ejes globales o en los ejes locales de la barra. Se debe considerar cuidadosamente la dirección de la imperfección, ya que la intención es aplicarla en la dirección general de la estructura para causar el mayor efecto desestabilizador. Una vez que se define esta información, la imperfección se puede asignar a varias barras, como a todos los pilares de la estructura.
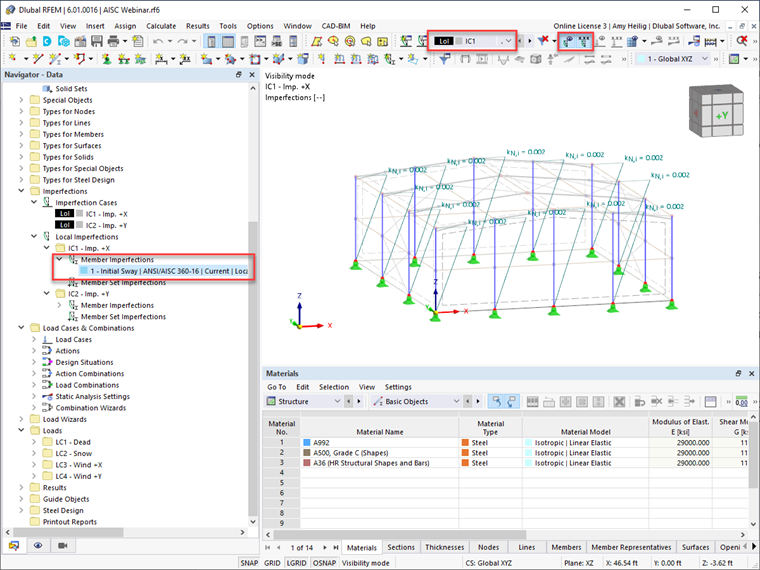
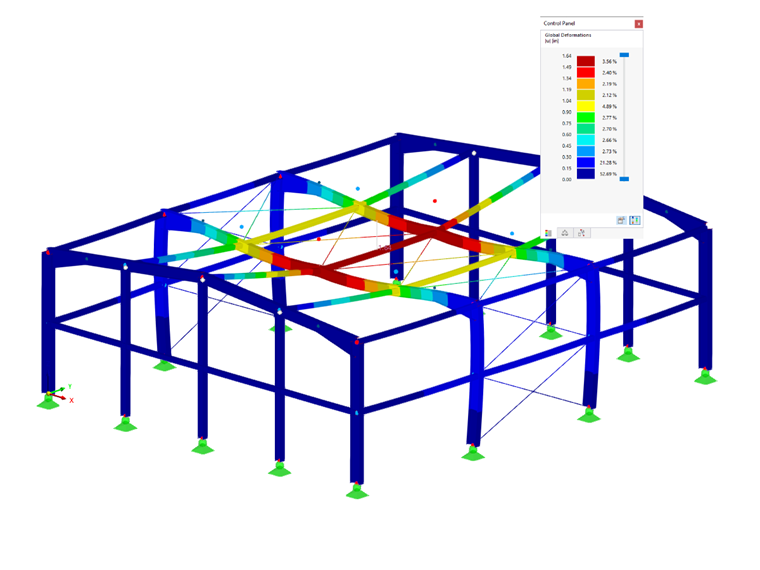
Una vez que se aplican las imperfecciones, se pueden ver gráficamente en la estructura en RFEM.
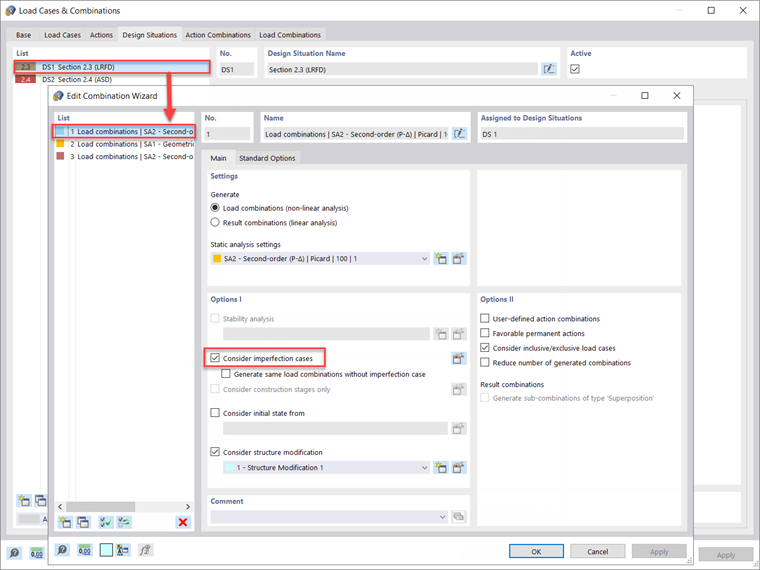
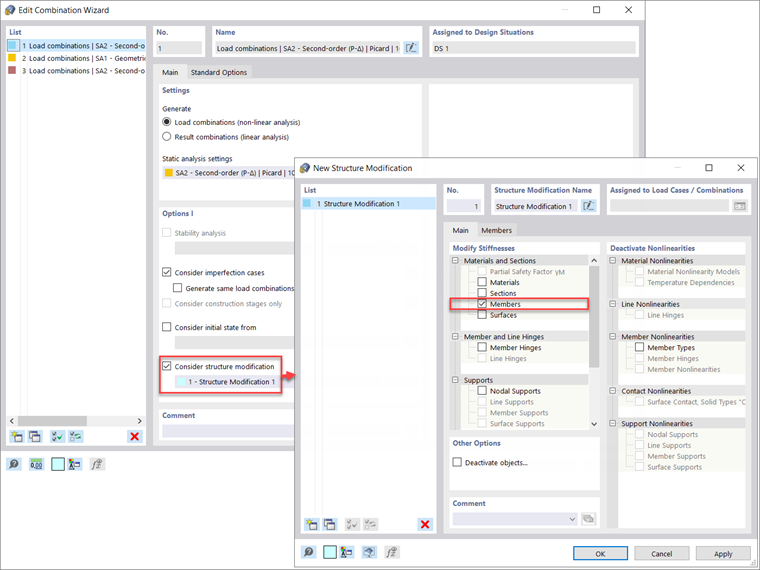
Las imperfecciones solo se deben aplicar a las combinaciones de carga de resistencia y no se requieren para las comprobaciones de servicio. Por lo tanto, en el cuadro de diálogo Editar asistente para combinaciones que se muestra anteriormente en la Imagen 1, se debe activar "Considerar casos de imperfección" y aplicar a la Situación de proyecto 1 - LRFD asumiendo que el cálculo de la resistencia se llevará a cabo según el método LRFD.
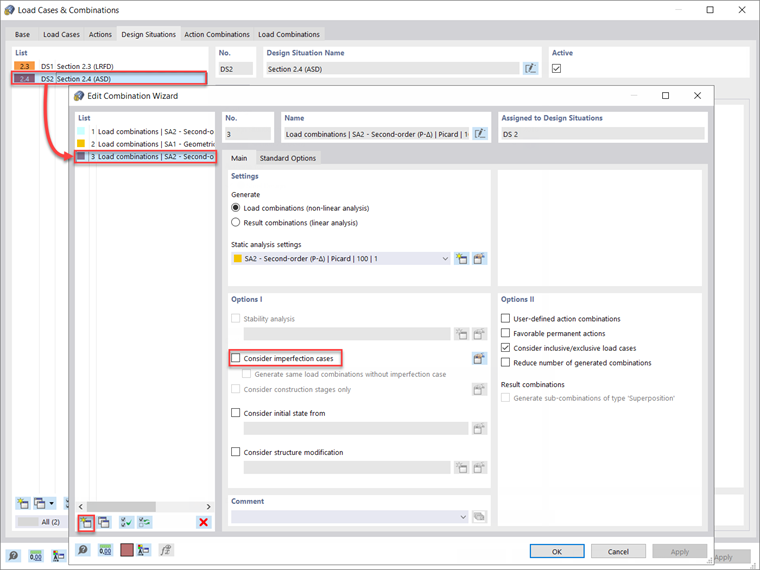
Alternativamente, el botón "Crear nuevo asistente para combinaciones" en la parte inferior izquierda se puede usar para generar una nueva definición de elemento con "Considerar casos de imperfección" desactivado. La configuración del análisis estático se establecerá en segundo orden (P-Δ) para el cálculo del estado límite de servicio de este ejemplo similar al cálculo de la resistencia. Ahora, este nuevo asistente para combinaciones se puede asignar a la situación de proyecto 2 - ASD suponiendo que el cálculo del estado límite de servicio se llevará a cabo utilizando las combinaciones de carga sin factorizar.
Una vez que se aplican estas configuraciones a las situaciones de proyecto, las combinaciones de carga individuales enumeradas en la pestaña "Combinaciones de carga" también reflejarán estas mismas configuraciones automáticamente.
Ajustes de rigidez
Las tensiones residuales de la barra pueden conducir a la fluencia parcial de la sección, produciendo un ablandamiento general de la estructura. Esto a su vez conduce a efectos desestabilizadores. Además, se debe considerar la distribución de la plasticidad a través de la sección de la barra y a lo largo de la longitud de la barra.
Para aproximar estos efectos en la reducción de la resistencia de la barra, AISC ha requerido que se aplique un factor de 0.8 a todas las rigideces que contribuyen a la estabilidad de la estructura. La norma continúa indicando en C2.3(a) [1], las reducciones de rigidez se deben aplicar a todas las barras para evitar la distorsión artificial de la estructura. Por lo tanto, este factor de 0.8 se puede aplicar a todas las rigideces axiales y a flexión de las barras.
Además, el factor τb calculado a partir de las ecuaciones. C2.2a y C2.2b [1] que se muestra a continuación se deben aplicar solo a la rigidez a flexión de las barras. Se deben considerar las secciones de elementos esbeltos frente a los no esbeltos para la resistencia a compresión de la sección.
- Cuando α Pr/Pns ≤ 0,5
- Cuando α Pr/Pns > 0,5
α
= 1,0 (LRFD); 1,60 (ASD)
Pr
Resistencia a compresión axial necesaria usando una combinación de carga LRFD o combinaciones de carga ASD, kips (N)
Pns
Resistencia a compresión de la sección;
- para secciones de elementos no esbeltos: Pns = Fy Ag,
- para secciones con elementos esbeltos: Pns = Fy Ae,
- donde Ae es como se define en la sección E7, kips (N)
Según la sección C2.3(c) [1], es admisible establecer τb = 1,0 para todas las rigideces a flexión de las barras, pero se debe aplicar una carga teórica adicional a la estructura definida por esto sección. Además, las reducciones de rigidez solo se aplican a los estados límite de resistencia y estabilidad. No es aplicable a los estados límite de servicio u otros análisis como la deriva, flecha, vibración y determinación del periodo.
RFEM 6 ofrece a los usuarios la capacidad de aplicar los requisitos de reducción de rigidez de AISC a las barras seleccionadas. El factor 0.8 se aplica a la rigidez axial y a flexión de la barra, mientras que el factor τb se puede calcular automáticamente a partir de las ecuaciones. C2.2a y C2.2b [1] y se aplica a la rigidez a flexión de la barra.
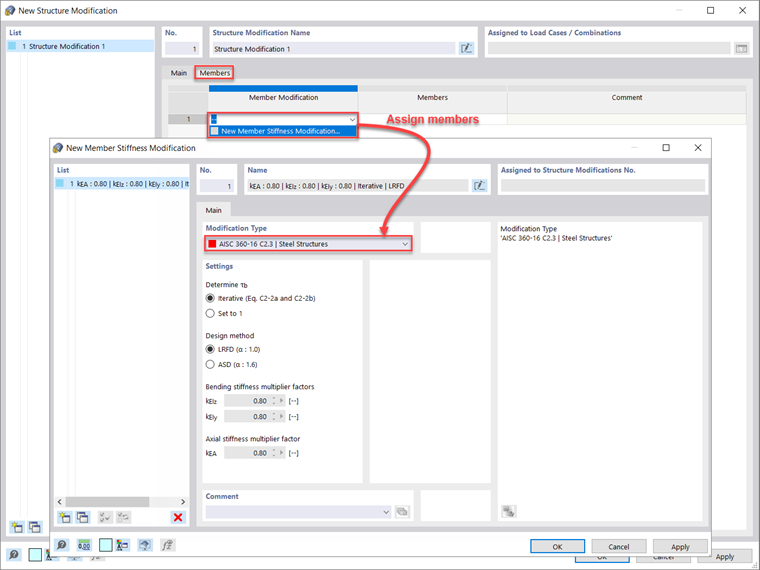
Al volver a visitar el asistente para combinaciones para la situación de proyecto 1 - LRFD, se debe activar "Considerar la modificación de la estructura" con una nueva configuración de modificación de la estructura definida. Una vez que también se activa la opción "Barras", está disponible una nueva pestaña Barras. Dentro de esta nueva pestaña, se puede seleccionar la "Nueva modificación de rigidez de barra". Esto abre la opción final para seleccionar el "AISC 360-16 C2.3 | Estructuras de acero" en el menú desplegable. Tenga en cuenta que las "Ecs. iterativas C2-2a y C2-2b” se selecciona para calcular automáticamente el factor de rigidez a flexión τb basado en el esfuerzo normal de los elementos esbeltos o no esbeltos. El factor 0.8 se establece de forma predeterminada y se aplica a la rigidez a flexión y axial. Una vez que se han definido todas las opciones, las barras de acero a las que se debe aplicar la reducción de rigidez se seleccionan gráficamente o los números de las barras se pueden introducir directamente en el cuadro de diálogo Modificación estructural.
Tenga en cuenta que el asistente para combinaciones separado que se definió previamente para la Situación de proyecto 2 - ASD para desactivar las opciones de imperfección para el cálculo del estado límite de servicio descrito anteriormente también debería dejar la opción "Considerar la modificación de la estructura" sin marcar. Esto utilizará las rigideces de la barra completa para todas las combinaciones de carga sin factorizar.
Observaciones finales
Los requisitos dados en AISC 360-16 Ch. C para el método de análisis directo, incluidos los efectos de segundo orden, las imperfecciones de las barras y las reducciones de rigidez, se pueden considerar en el análisis y diseño de RFEM 6 utilizando los flujos de trabajo descritos anteriormente. Para obtener más información y ejemplos sobre la aplicación del método de análisis directo en RFEM, consulte el seminario web previamente grabado Cáculo de acero con AISC 360-16 en RFEM 6 y descargue el modelo relacionado en Modelos para descargar.
- Seminario web | Cálculo de acero según AISC 360-16 en RFEM 6 (Estados Unidos)
- Modelo para descarga | Estructura de nave de acero | AISC 360-16