Wymagania dotyczące stateczności
W sek. C1 [1] , podczas obliczania stateczności konstrukcji stalowej wymieniono pięć wymagań. Bezpośrednio z AISC 360-16 są to:
- Odkształcenia na zginanie, ścinanie i osiowe prętów oraz wszystkie inne odkształcenia elementów i połączeń, które mają wpływ na przemieszczenia konstrukcji
- Efekty drugiego rzędu (w tym efekty P-Δ i P-δ)
- Imperfekcje geometryczne
- Redukcje sztywności ze względu na niesprężystość, z uwzględnieniem wpływu częściowego uplastycznienia przekroju, które może być uwydatnione przez występowanie naprężeń własnych
- Niepewność wytrzymałości i sztywności układu, pręta i połączenia
W celu spełnienia powyższych wymagań można zastosować metodę analizy bezpośredniej. W tym artykule skupimy się głównie na punktach b do d oraz zastosowaniu w programie RFEM 6.
efekty drugiego rzędu
Analiza konstrukcji powinna uwzględniać efekty drugiego rzędu, w tym P-Δ i P-δ. Jeżeli element konstrukcyjny, taki jak słup, jest dodatkowo obciążony obciążeniem osiowym, zostanie ugięty. Odległość ugięcia Δ pomnożona przez przyłożone obciążenie osiowe P tworzy moment drugorzędny P-Δ, który należy uwzględnić. Dodatkowo w analizie należy również uwzględnić destabilizujący wpływ obciążenia osiowego działającego wzdłuż odkształconej krzywizny pręta, czyli P-δ. Rys. W C-C2.1 [1] przedstawiono graficzny przykład takich efektów drugorzędnych na pręcie.
AISC wymienia warunki w C2.1(b) [1] , w których efekty P-δ mogą być całkowicie pominięte. W przeciwnym razie, jeżeli pręt jest poddany zarówno ściskaniu, jak i zginaniu, lokalne odkształcenia powinny zostać uwzględnione w analizie.
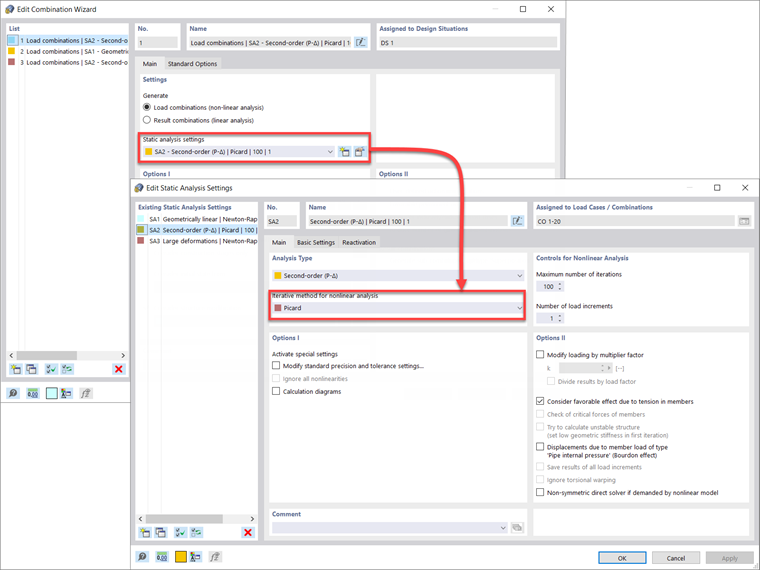
W programie RFEM 6 analiza drugiego rzędu jest rozwiązywana iteracyjnie jako sekwencja problemów liniowych, w których siła osiowa jest aktualizowana z poprzedniej iteracji i traktowana jako stała w kroku iteracji. Jest to metoda iteracyjna dla punktów stałych, znana jako metoda Picarda. W przypadku wybrania tej metody efekty drugorzędne P-Δ i P-δ są automatycznie rejestrowane w równaniach różniczkowych w solwerze RFEM 6.
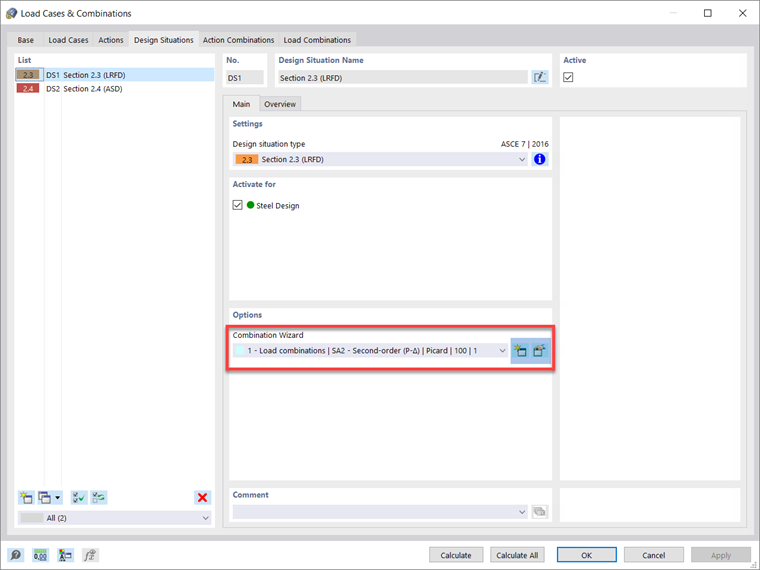
Sytuacje obliczeniowe i kombinacje obciążeń w programie RFEM 6 są domyślnie ustawione jako drugiego rzędu i metoda Picarda. Użytkownik może modyfikować te domyślne ustawienia dla sytuacji obliczeniowych LRFD lub ASD, na przykład w oknie dialogowym Generator kombinacji – Ustawienia analizy statycznej – Metoda iteracyjna dla analizy nieliniowej.
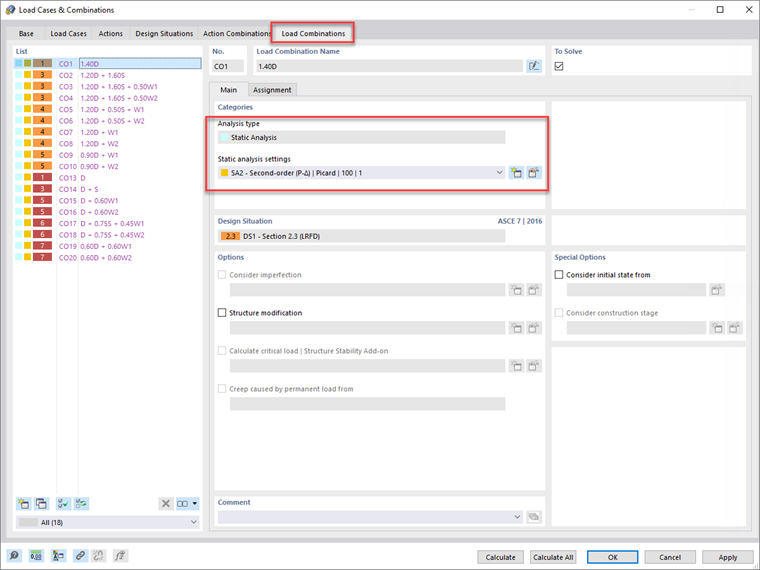
Poszczególne kombinacje obciążeń będą zgodne z ustawieniami analizy zdefiniowanymi w odpowiedniej sytuacji obliczeniowej. W razie potrzeby użytkownik może jednak indywidualnie modyfikować ustawienia kombinacji obciążeń.
Zgodnie z rozdz. C2.1(b) [1] , użytkownik może zachować domyślną analizę drugiego rzędu dla sytuacji obliczeniowej 1 - LRFD, która będzie stosowana do obliczeń wytrzymałościowych. Dodatkowo, żądany typ analizy można wybrać dla sytuacji obliczeniowej 2 - ASD, którą można wykorzystać do sprawdzenia stanu granicznego użytkowalności wraz z innymi utworzonymi sytuacjami obliczeniowymi. Więcej informacji na temat opcji dostępnych w tych oknach dialogowych można znaleźć w instrukcji online programu RFEM 6 - Ustawienia analizy statycznej.
Imperfekcje geometryczne
Sek. C2.2 [1] wymaga uwzględnienia imperfekcji konstrukcji poprzez bezpośrednie modelowanie imperfekcji lub poprzez zastosowanie obciążeń hipotetycznych. AISC wyjaśnia również, że głównym problemem związanym z imperfekcjami w konstrukcjach budowlanych jest przechyły słupów. Wymiarowanie pręta nie jest wymagane w tym przekroju, ponieważ efekt ten jest uwzględniony w rozdz. E [1] dla obliczeń na ściskanie.
Aby uzyskać jak największy efekt destabilizacji, modelowanie bezpośrednie imperfekcji powinno uwzględniać początkowe przemieszczenia wywołane obciążeniem i kształtami wyboczeniowymi W zależności od rozmiaru konstrukcji może to być czasochłonne i skomplikowane. Zamiast tego można zastosować alternatywną metodę z przyłożonymi obciążeniami hipotetycznymi.
Zgodnie z C2.2b(a) [1] obciążenia hipotetyczne należy przykładać jako addytywne obciążenia boczne na wszystkich poziomach we wszystkich kombinacjach obciążeń. Wyjątek podany w C2.2b(d) [1] obejmuje sytuacje, w których dryft konstrukcji drugiego rzędu do dryftu pierwszego rzędu jest równy lub mniejszy niż 1,7; wówczas obciążenia hipotetyczne mogą zostać przyłożone do kombinacji obciążeń wyłącznie grawitacyjnych i mogą zostać wyłączone z kombinacji z innymi przyłożonymi obciążeniami bocznymi.
Umowną wielkość obciążenia na każdym poziomie można obliczyć za pomocą równania C2-1 [1].
Gdzie
α = 1,0 (LRFD); α = 1,60 (ASD)Ni = obciążenie hipotetyczne przyłożone na poziomie i , kips (N)
Yi = obciążenie grawitacyjne przyłożone na poziomie i z kombinacji obciążeń LRFD lub kombinacji obciążeń ASD, kips (N)
Obciążenia hipotetyczne należy przykładać w kierunku wywołującym największy efekt destabilizujący. Oznacza to, że w przypadku kombinacji obciążeń działających wyłącznie na zasadzie grawitacji należy przyłożyć obciążenia hipotetyczne w obu kierunkach ortogonalnych. W przypadku kombinacji obciążeń, w których przyłożone są obciążenia boczne, obciążenia hipotetyczne powinny być przyłożone w tym samym kierunku wypadkowym (np. obciążenia wiatrem w kierunku X powinny obejmować obciążenia hipotetyczne w kierunku X).
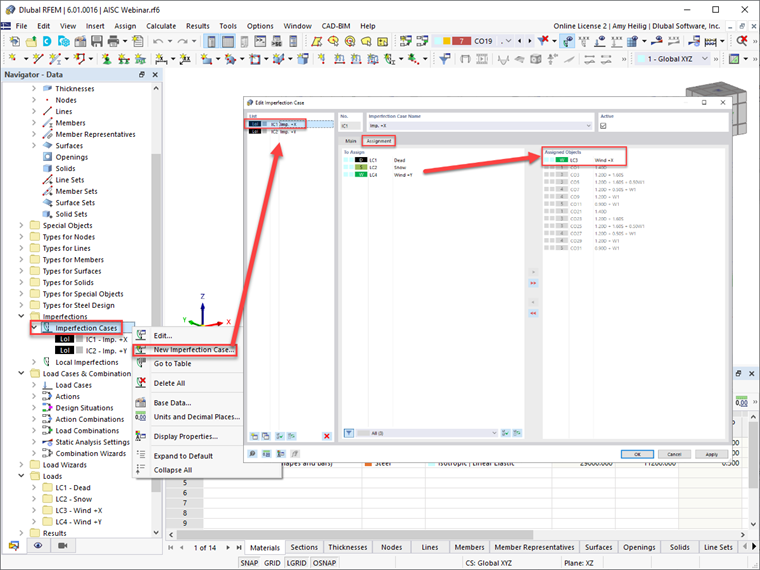
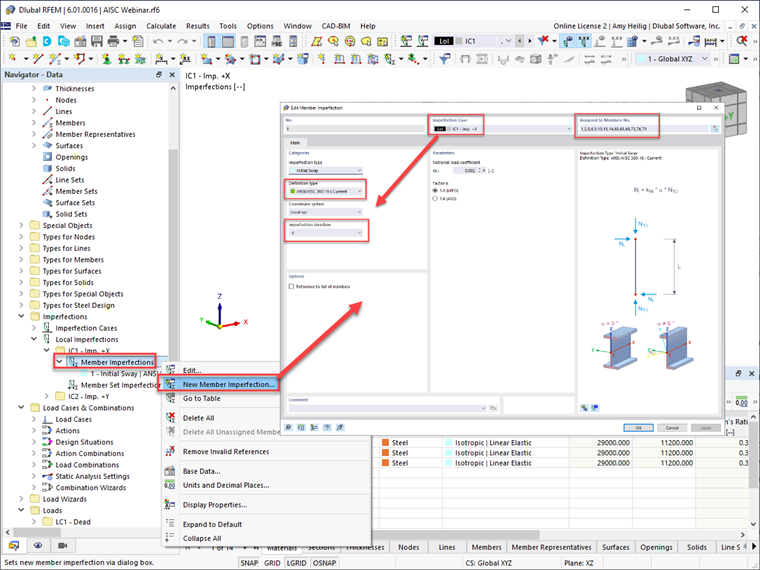
Program RFEM 6 zapewnia użytkownikom możliwość definiowania przypadków imperfekcji w kierunkach ortogonalnych, na przykład w kierunkach ±X lub ±Y. Przypadki obciążenia można następnie przypisać do każdego przypadku obciążenia imperfekcją, z uwzględnieniem największego efektu destabilizującego. Program RFEM automatycznie przydzieli przypadek imperfekcji do wygenerowanych kombinacji obciążeń, jak pokazano w tym oknie dialogowym.
Po zdefiniowaniu przypadków imperfekcji użytkownik musi zdefiniować imperfekcje pręta w każdym przypadku imperfekcji. „ANSI/AISC 360-16 | Bieżące” w rozwijanym menu uwzględni siłę osiową pręta z przypisanej kombinacji obciążeń, zastosuje równ. C2-1 [1] i zastosować obliczoną hipotetyczną wielkość obciążenia zarówno na początku, jak i na końcu pręta. „ANSI/AISC 360-16 | Obciążenie grawitacyjne” pozwoli użytkownikowi na odniesienie się do innej kombinacji obciążeń niż aktualna w celu obliczenia siły osiowej pręta. Należy również określić kierunek imperfekcji w oparciu o osie globalne lub osie lokalne pręta. Należy zwrócić szczególną uwagę na kierunek imperfekcji, ponieważ intencją jest, aby konstrukcja miała wywołać największy efekt destabilizujący. Po zdefiniowaniu tych informacji imperfekcję można przypisać do wielu prętów, na przykład do wszystkich słupów w konstrukcji.
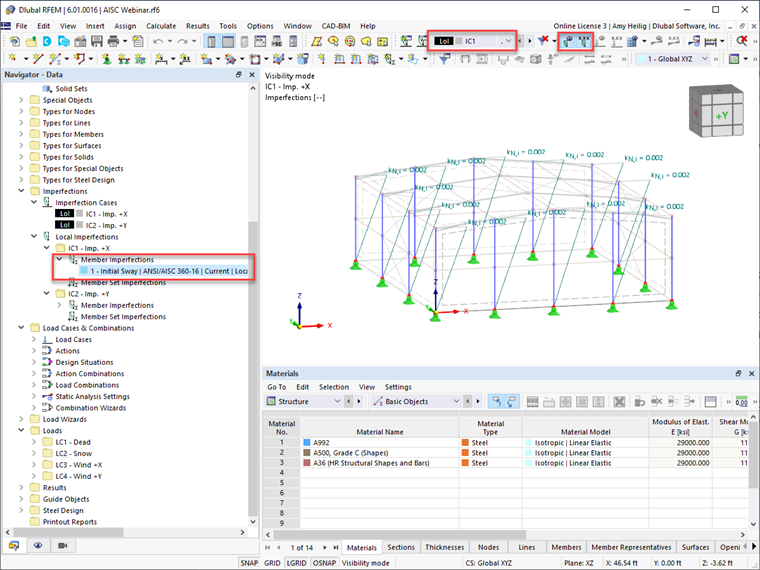
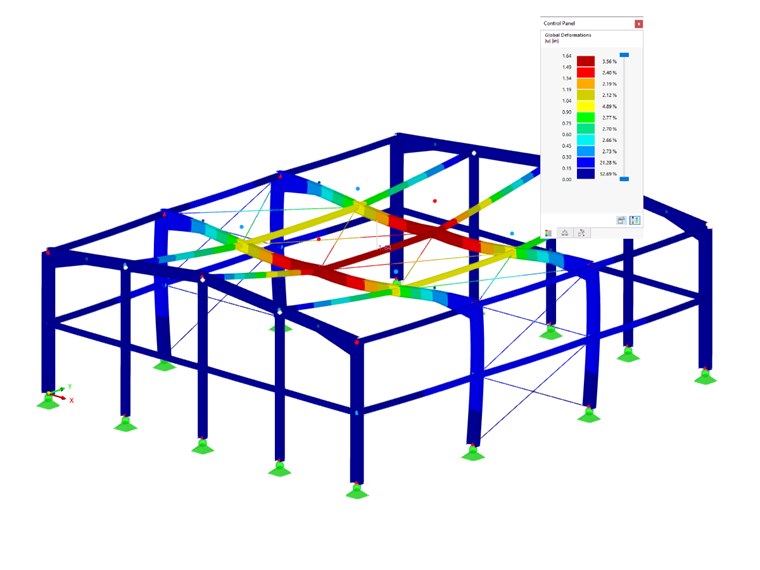
Po zastosowaniu imperfekcji można je zobaczyć graficznie na konstrukcji w programie RFEM.
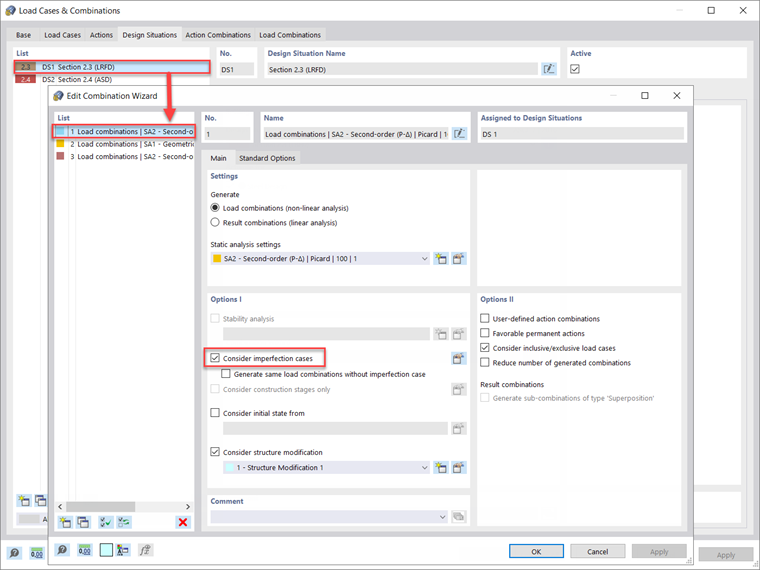
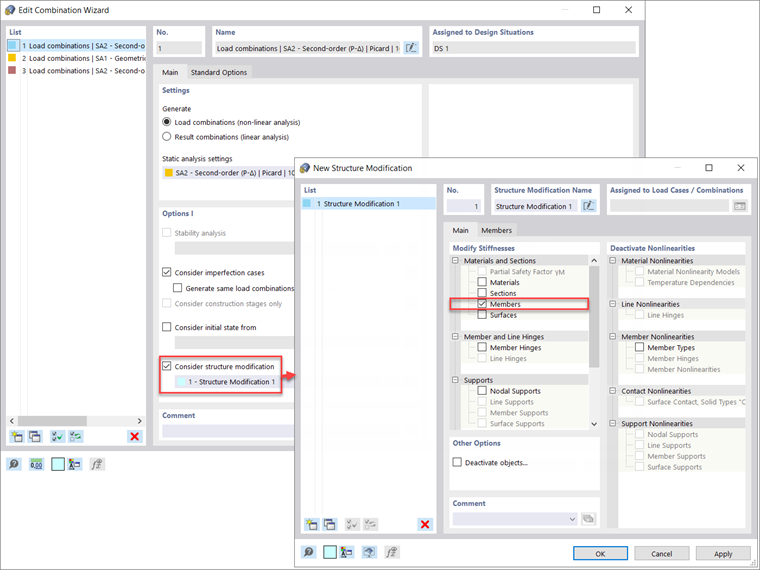
Imperfekcje należy stosować tylko w kombinacjach obciążeń i nie są wymagane do sprawdzenia stanu granicznego użytkowalności. Dlatego w oknie dialogowym Edytuj generator kombinacji , pokazanym wcześniej na rysunku 1, należy włączyć opcję „Uwzględnij przypadki imperfekcji” i zastosować do sytuacji obliczeniowej 1 - LRFD, przy założeniu, że obliczenia wytrzymałościowe zostaną przeprowadzone zgodnie z metodą LRFD. 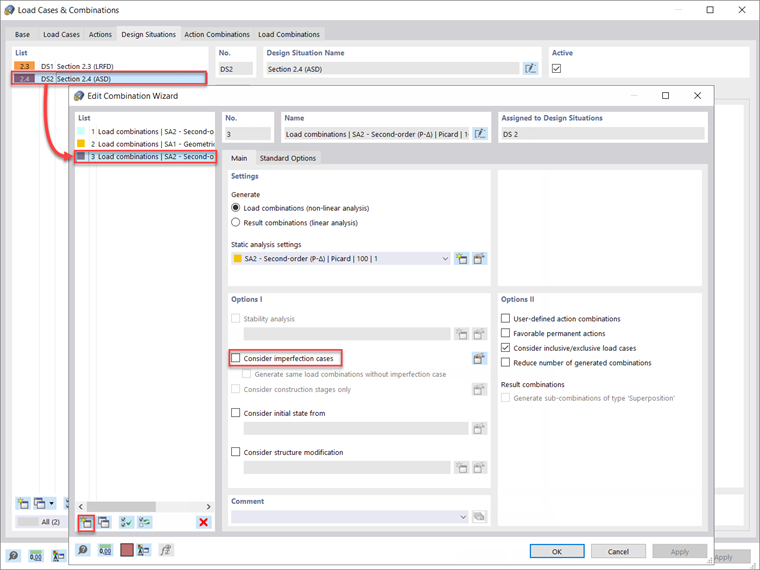Alternatywnie, za pomocą przycisku „Utwórz nowy generator kombinacji” w lewym dolnym rogu można wygenerować nową definicję elementu z wyłączoną opcją „Uwzględnij przypadki imperfekcji”. W tym przykładzie, obliczenia stanu granicznego użytkowalności, podobnie jak obliczenia wytrzymałościowe, zostaną przeprowadzone według teorii drugiego rzędu (P-Δ). Teraz ten nowy generator kombinacji może być przypisany do sytuacji obliczeniowej 2 - ASD, przy założeniu, że obliczenia stanu granicznego użytkowalności zostaną przeprowadzone z wykorzystaniem nieobliczonych kombinacji obciążeń.
Po zastosowaniu tych ustawień w sytuacjach obliczeniowych poszczególne kombinacje obciążeń wymienione w zakładce „Kombinacje obciążeń” również automatycznie odzwierciedlają te same ustawienia.
Dostosowanie sztywności
Naprężenia szczątkowe w pręcie mogą prowadzić do częściowego uplastycznienia przekroju, powodującego ogólne rozmiękczenie konstrukcji. To z kolei prowadzi do efektów destabilizujących. Dodatkowo należy uwzględnić rozkład plastyczności w przekroju i na długości pręta.
Aby przybliżyć te wpływy na redukcję wytrzymałości prętów, AISC wymagało zastosowania współczynnika 0,8 do wszystkich sztywności wpływających na stateczność konstrukcji. W dalszej części normy w C2.3(a) [1] należy zastosować redukcje sztywności dla wszystkich prętów w celu uniknięcia sztucznego odkształcenia konstrukcji. Dzięki temu współczynnik 0,8 może być zastosowany do wszystkich sztywności osiowej i na zginanie wszystkich prętów.
Dodatkowo, współczynnik τb obliczony na podstawie Równań. Pokazane poniżej normy C2.2a i C2.2b [1] należy zastosować tylko do sztywności prętów na zginanie. Przy obliczaniu wytrzymałości przekroju na ściskanie należy uwzględnić przekroje smukłe w porównaniu z przekrojami niesmukłymi.
(1) Jeżeli α Pr/Pns ≤ 0.5
(2) Jeżeli α Pr/Pns > 0.5
Gdzie
α = 1,0 (LRFD); α = 1,60 (ASD)Pr = wymagana wytrzymałość na ściskanie osiowe według kombinacji obciążeń LRFD lub kombinacji obciążeń ASD, kips (N)
Pns = wytrzymałość przekroju na ściskanie; dla przekrojów niesmukłych Pns = Fy Ag, a dla przekrojów smukłych Pns = Fy Ae , gdzie Ae jest takie, jak zdefiniowano w Przekrój E7, kips (N)
Zgodnie z rozdz. C2.3(c) [1] dopuszcza się, aby dla sztywności na zginanie wszystkich prętów zadać τb = 1.0, ale do konstrukcji należy przyłożyć dodatkowe obciążenie hipotetyczne, zdefiniowane w tym rozdziale. Dodatkowo, redukcje sztywności są stosowane tylko w stanach granicznych wytrzymałości i stateczności. Nie można jej zastosować do analizy stanów granicznych użytkowalności ani innych analiz, takich jak wyznaczanie dryftu, ugięcia, drgań i okresu.
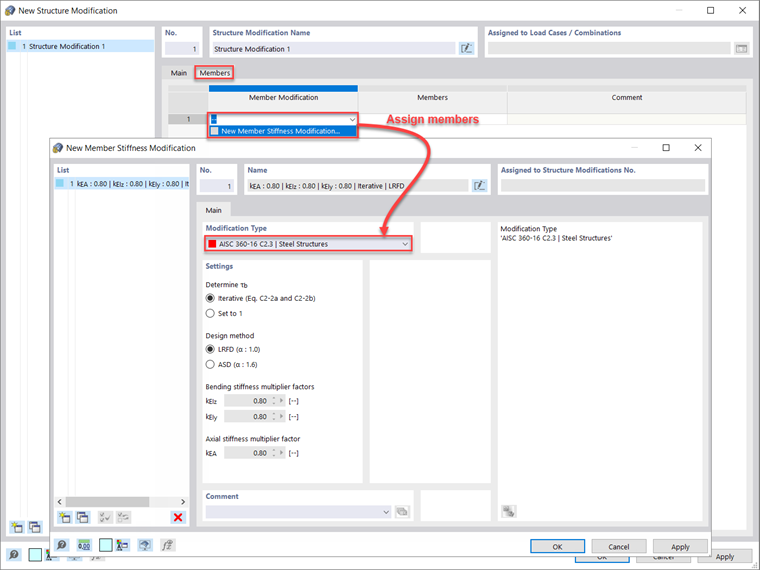
Program RFEM 6 daje użytkownikom możliwość zastosowania wymagań redukcji sztywności według AISC do wybranych prętów. Współczynnik 0,8 jest stosowany do sztywności osiowej i sztywności na zginanie pręta, podczas gdy współczynnik τb może być obliczany automatycznie na podstawie równań. C2.2a i C2.2b [1] i zastosowane do obliczenia sztywności pręta na zginanie. Wracając do generatora kombinacji dla sytuacji obliczeniowej 1 - LRFD, należy aktywować opcję „Uwzględnij modyfikację konstrukcji” ze zdefiniowanym nowym ustawieniem modyfikacji konstrukcji. Po aktywowaniu opcji „Pręty” dostępna jest nowa zakładka Pręty. W tej nowej zakładce można wybrać „Nową modyfikację sztywności pręta”. Pojawi się ostatnia opcja wyboru „AISC 360-16 C2.3 | Konstrukcje stalowe”. Zwróć uwagę, że „Równania iteracyjne C2-2a i C2-2b” w celu automatycznego obliczania współczynnika sztywności na zginanie τb na podstawie siły osiowej smukłych lub niesmukłych elementów. Współczynnik 0,8 jest ustawiony domyślnie i stosowany dla sztywności na zginanie oraz sztywności osiowej. Po zdefiniowaniu wszystkich opcji pręty stalowe, do których ma zostać zastosowana redukcja sztywności, są wybierane graficznie lub numery prętów mogą być ponownie wprowadzane bezpośrednio w oknie dialogowym Modyfikacja konstrukcji.
Należy pamiętać, że za pomocą osobnego Generatora kombinacji, który został wcześniej zdefiniowany dla sytuacji obliczeniowej 2 - ASD, w celu dezaktywacji opcji imperfekcji dla obliczeń stanu granicznego użytkowalności, opisanych powyżej, również nie powinno być zaznaczone pole wyboru „Uwzględnij modyfikację konstrukcji”. Spowoduje to wykorzystanie sztywności całego pręta dla wszystkich niewymienionych kombinacji obciążeń.
Uwagi końcowe
Wymagania podane w AISC 360-16 Ch. C dla metody bezpośredniej, w tym efekty drugiego rzędu, imperfekcje prętów i redukcje sztywności, mogą być uwzględnione w analizie i wymiarowaniu w programie RFEM 6 za pomocą procesów roboczych opisanych powyżej. Więcej informacji i przykłady na temat zastosowania metody bezpośredniej w RFEM można znaleźć w webinarium AISC 360-16 Projektowanie konstrukcji stalowych w RFEM 6 , dostępnym do pobrania w sekcji Modele do pobrania.
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
