Concrete Column Analysis
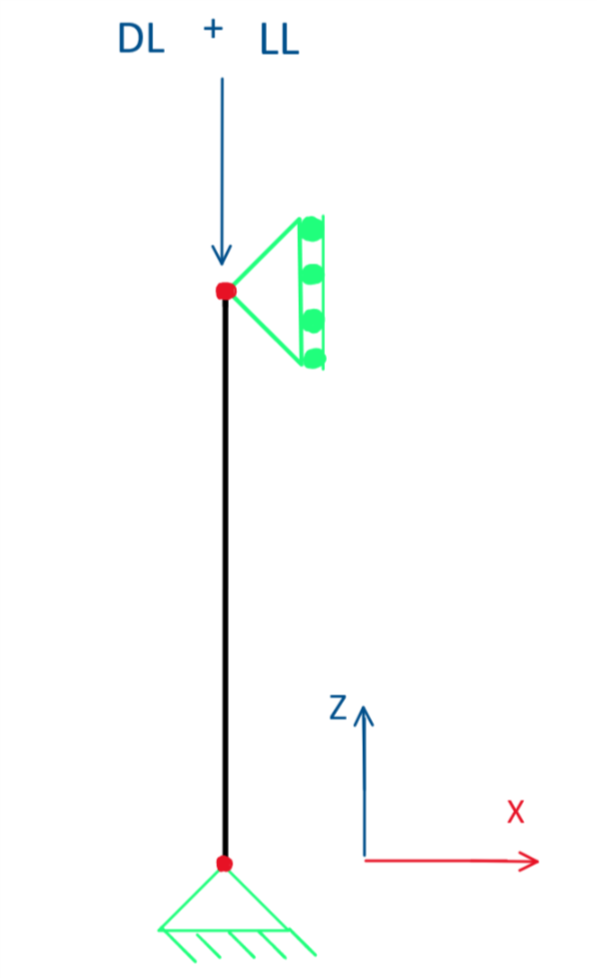
A reinforced square tie concrete column is designed to support an axial dead load and live load of 135 and 175 kips, respectively, using ULS design and factored LRFD load combinations according to ACI 318-19 [1] as presented in Image 01. The concrete material has a compressive strength f'c of 4 ksi while the reinforcing steel has a yield strength fy of 60 ksi. The steel reinforcement percentage is initially assumed to be 2%.
Dimension Design
To begin, the dimensions of the cross-section must be calculated. The square tie column is determined to be compression controlled, since all axial loads are strictly in compression. As per Table 21.2.2 [1], the strength reduction factor Φ is equal to 0.65. When determining the maximum axial strength, Table 22.4.2.1 [1] is referenced which sets the alpha factor (α) equal to 0.80. Now, the design load Pu can be calculated.
Pu = 1.2 (135 k) + 1.6 (175 k)
Based on these factors, Pu is equal to 442 kips. Next, the gross cross-section Ag can be calculated utilizing Eqn. 22.4.2.2.
Pu = (Φ) (α) [0.85 f’c (Ag - Ast) + fy Ast]
442k = (0.65) (0.80) [0.85 (4 kips) (Ag - 0.02 Ag) + ((60 ksi) (0.02) Ag)]
Solving for Ag, we receive an area of 188 in². The square root of Ag is taken and rounded up to set a cross-section of 14" x 14" for the column.
Required Steel Reinforcement
Now that Ag is established, the steel reinforcement area Ast can be calculated utilizing Eqn. 22.4.2.2 by substituting the known value of Ag = 196 in² and solving
442k = (0.65) (0.80) [0.85 (4 kips) (196 in² - Ast) + ((60 ksi) (Ast))]
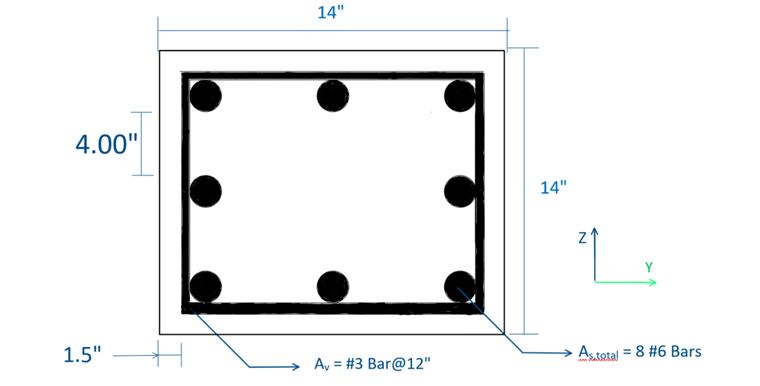
Solving for Ast yields a value of 3.24 in². From this, the number of bars required for design can be found. According to Sec. 10.7.3.1 [[#Refer [1]]], a square tie column is required to have at least four bars. Based on these criteria, and the minimum required area of 3.24 in², (8) No. 6 bars for the steel reinforcement are used from Appendix A [1]. This provides the reinforcement area below.
Ast = 3.52 in²
Tie Selection
Determining the minimum tie size requires Sec. 25.7.2.2 [1]. In the previous section, we selected No. 6 longitudinal bars, which are smaller than No. 10 bars. Based on this information and section, we select No. 3 for the ties.
Tie Spacing
To determine the minimum tie spacing(s), we refer to Sec. 25.7.2.1 [1]. Ties that consist of closed looped deformed bars must have spacing that is in accordance with (a) and (b) from this section.
(a) The clear spacing must be equal to or greater than (4/3) dagg. For this calculation, we will be assuming an aggregate diameter (dagg) of 1.00 inch.
smin = (4/3) dagg = (4/3) (1.00 in) = 1.33 in
(b) The center-to-center spacing should not exceed the minimum of 16db of the longitudinal bar diameter, 48db of the tie bar, or the smallest dimension of the member.
sMax = Min (16db, 48db, 14 in)
16db = 16 (0.75 in.) = 12 in
48db = 48 (0.375 in.) = 18 in
The minimum clear tie spacing calculated is equal to 1.33 inches and the maximum tie spacing calculated is equal to 12 inches. For this design, a maximum of 12 inches for the tie spacing will govern.
Detailing Check
The detailing check can now be performed to verify the reinforcement percentage. The required steel percentage must be between 1% and 8% based on the ACI 318-14 [1] requirements to be adequate.
Steel Percentage =
|
Ast |
Total area of nonprestressed longitudinal reinforcement including bars or steel shapes, and excluding prestressing reinforcement |
|
Ag |
Gross cross-section |
Longitudinal Bar Spacing
The maximum longitudinal bar spacing can be calculated on the basis of the clear cover spacing and the diameter of both the tie and longitudinal bars.
Maximum longitudinal bar spacing:
4.00 inches is less than 6 inches, which is required as per 25.7.2.3 (a) [1]. O.K.
The minimum longitudinal bar spacing can be calculated by referencing 25.2.3 [1], which states that the minimum longitudinal spacing for columns must be at least the greatest of (a) through (c).
- (a) 1.5 in
- (b) 1.5 db = 1.5 (0.75 in) = 1.125 in
- (c) (4/3) db = (4/3) (1.00 in) = 1.33 in
Therefore, the minimum longitudinal bar spacing is equal to 1.50 inches.
The development length (Ld) must also be calculated with reference to 25.4.9.2 [1]. This will be equal to the greater of (a) or (b) calculated below.
- (a)
fy
Specified yield strength for non-prestressed reinforcement
ψr
Factor used to modify development length based on confining reinforcement
λ
Modification factor to reflect the reduced mechanical properties of lightweight concrete relative to normal weight concrete of the same compressive strength
f'c
Compressive strength
db
Nominal diameter of bar, wire, or prestressing strand
- (b)
fy
Specified yield strength for non-prestressed reinforcement
ψr
Factor used to modify development length based on confining reinforcement
db
Nominal diameter of bar, wire, or prestressing strand
In this example, (a) is the greater value, so Ldc = 14.23 inches.
Referencing 25.4.10.1 [1], the development length is multiplied by the ratio of required steel reinforcement over provided steel reinforcement.
The reinforced square tie column is fully designed, and its cross-section can be viewed below in Image 02.
Comparison with RFEM
An alternative to designing a square tie column manually is to utilize the add-on module RF-CONCRETE Members and perform the design as per ACI 318-14 [1]. The module will determine the required reinforcement to resist the applied loads on the column. Furthermore, the program will design the provided reinforcement based on the given axial loads on the column while taking into consideration the spacing requirements from the standard. The user can make minor adjustments to the provided reinforcement layout in the results table.
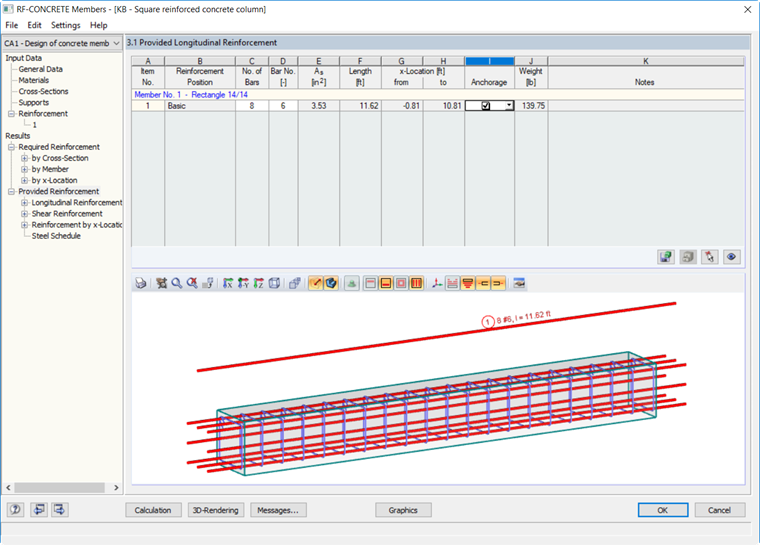
Based on the applied loads for this example, RF-CONCRETE Members has determined a required longitudinal bar reinforcement area of 1.92 in² and a provided area of 3.53 in². The development length calculated in the add-on module is equal to 0.81 ft. The discrepancy in comparison with the development length calculated above with analytical equations is due to the program's non-linear calculations, including the partial factor γ. The factor γ is the ratio of ultimate and acting internal forces taken from RFEM. The development length in RF-CONCRETE Members is found by multiplying the reciprocal value of gamma by the length determined from 25.4.9.2 [1]. More info on this non-linear calculation can be found in the RF-CONCRETE Members help file linked below. This reinforcement can be previewed in Image 03.
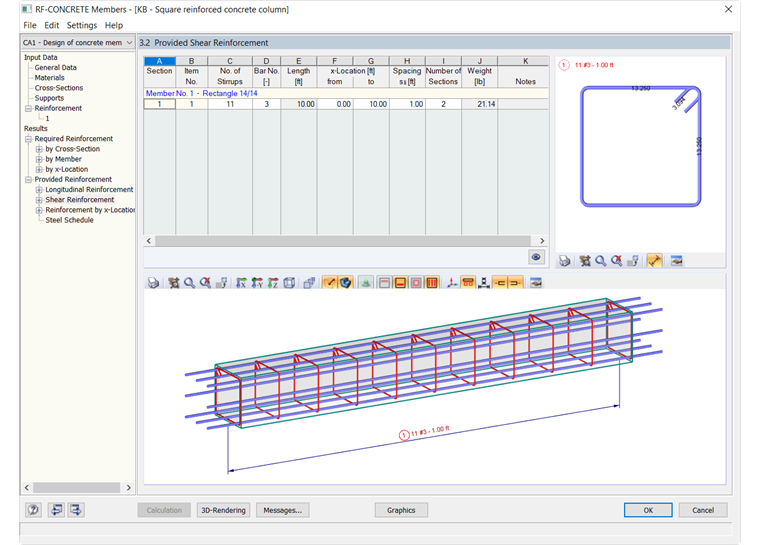
The provided shear reinforcement for the member within RF-CONCRETE Members was calculated to be (11) No. 3 bars with a spacing (s) of 12 inches. The provided shear reinforcement layout is shown below in Image 04.