Posouzení železobetonového sloupu
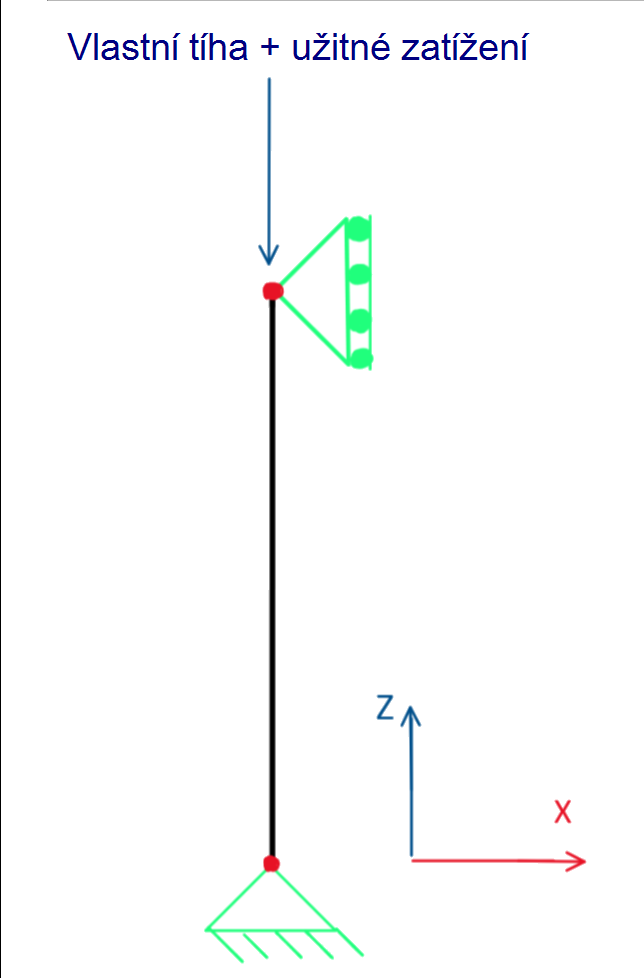
Železobetonový čtvercový sloup vyztužený třmínky je navržen tak, aby unesl vlastní tíhu 135 kips a užitné zatížení 175 kips, a to pomocí posouzení v MSÚ a zohlednění kombinací zatížení LRFD podle ACI 318-19 [1] (obrázek 1). Beton má pevnost v tlaku f'c = 4 ksi, zatímco výztužná ocel má mez kluzu fy = 60 ksi. Procento vyztužení se zpočátku uvažuje 2%.
Návrh rozměrů
Nejdříve je třeba spočítat rozměry průřezu. Čtvercový sloup s třmínky bude posuzován na tlak, protože všechna normálová zatížení jsou striktně tlaková. V tabulce 21.2.2 [1] se součinitel redukce pevnosti Φ rovná 0,65. Při výpočtu maximální normálové pevnosti se vychází z tabulky 22.4.2.1 [1] , v níž se součinitel alfa (α) rovná 0,80. Nyní můžeme vypočítat návrhové zatížení Pu.
Pu = 1,2 (135 k) + 1,6 (175 k)
Na základě těchto součinitelů se Pu rovná 442 kips. Dále lze vypočítat neoslabený průřez Ag pomocí rovnice 22.4.2.2.
Pu = (Φ) (α) [0,85 f’c (Ag - Ast) + fy Ast]
442k = (0,65) (0,80) [0,85 (4 kips) (Ag - 0,02 Ag) + ((60 ksi) (0,02) Ag)]
Řešením je plocha Ag = 188 in2. Plochu Ag odmocníme a zaokrouhlíme nahoru, a tak dostaneme průřez sloupu 14 ”x 14“.
Nutná ocelová výztuž
Nyní, když je stanovena Ag, lze vypočítat plochu výztuže Ast pomocí rovnice 22.4.2.2 dosazením známé hodnoty Ag = 196 in2 a řešením
442k = (0,65) (0,80) [0,85 (4 kips) (196 in2 - Ast) + ((60 ksi) (Ast))]
Výsledkem je Ast = 3,24 in2. Z toho lze určit počet potřebných prutů výztuže. Podle čl. 10.7.3.1 [1] musí mít čtvercový třmínkový sloup alespoň čtyři pruty. Na základě tohoto kritéria a minimální nutné plochy 3,24 in2 se pro ocelovou výztuž použije (8) prutů č. 6 podle přílohy A [1]. Tím dostaneme níže uvedenou plochu výztuže.
Ast = 3,52 in2
Výběr třmínků
Pro stanovení minimální velikosti třmínku je třeba postupovat podle čl. 25.7.2.2 [1]. Výše jsme vybrali podélné pruty č. 6, které jsou menší než pruty č. 10. Na základě těchto informací a průřezu vybereme pro třmínky pruty č. 3.
Vzdálenosti třmínků
Pro stanovení minimální vzdálenosti třmínků odkazujeme na čl. 25.7.2.1 [1]. Třmínky, které jsou tvořeny pruty tvarovanými do uzavřených smyček, musí mít mezi sebou vzdálenost, která je v souladu s (a) a (b) v tomto odstavci.
(a) světlá vzdálenost musí být rovna nebo větší než (4/3) dagg. Pro tento výpočet budeme uvažovat průměr kameniva (dagg) = 1 in.
smin = (4/3) dagg = (4/3) (1,00 in) = 1,33 in
(b) Vzdálenost mezi středy by neměla překročit minimálně 16db průměru podélného prutu výztuže, 48db průměru třmínku nebo nejmenší rozměr prutu.
sMax = Min (16db, 48db, 14 in)
16db = 16 (0.75 in.) = 12 in
48db = 48 (0.375 in.) = 18 in
Minimální vypočítaná světlá vzdálenost třmínků je 1,33 in a maximální vypočítaná vzdálenost třmínků je 12 in. U tohoto posouzení bude rozhodující maximální vzdálenost mezi třmínky 12 in.
Posouzení detailů
Nyní je možné provést posouzení detailů pro ověření procenta vyztužení. Nutné procento vyztužení musí být podle normy ACI 318-14 [1] v rozmezí 1% až 8%.
Procento vyztužení ocelí =
OKVzdálenosti podélných prutů
Maximální vzdálenost mezi podélnými pruty lze vypočítat na základě světlé vzdálenosti krytí a průměru podélné výztuže a třmínků.
Maximální vzdálenost podélných prutů výztuže:
4 in je méně než 6 in, které jsou vyžadovány podle 25.7.2.3 (a) [1]. OK
Minimální vzdálenost mezi podélnými pruty lze vypočítat pomocí čl. 25.2.3 [1], který uvádí, že minimální podélná vzdálenost pro sloupy musí být přinejmenším největší z hodnot (a) až (c).
(a) 1,5 in
(b) 1,5 db = 1,5 (0,75 in) = 1,125 in
(c) (4/3) db = (4/3) (1,00 in) = 1,33 in
Minimální vzdálenost podélných prutů je tak 1,50 in.
Podle 25.4.9.2 [1] je také třeba spočítat kotevní délku (Ld). Ta se bude rovnat větší z (a) nebo (b) vypočítaných níže.
(a)
(b)
V tomto příkladu je (a) větší, takže Ldc = 14,23 in.
Podle 25.4.10.1 [1] se kotevní délka vynásobí poměrem nutné výztuže ku navržené výztuži.
.
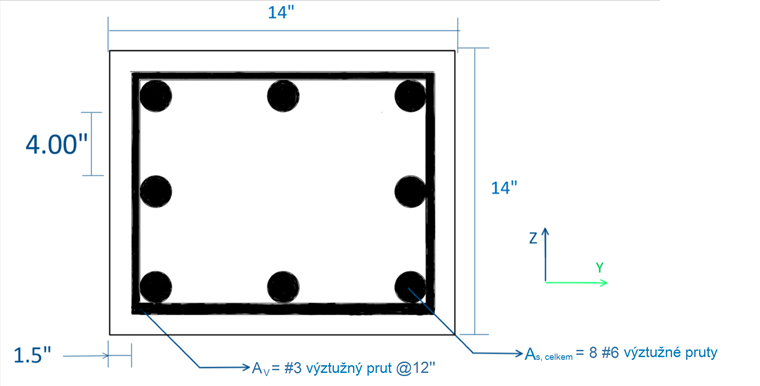
Třmínky vyztužený čtvercový sloup je kompletně navržen a jeho průřez lze vidět na obrázku 2.
Porovnání s programem RFEM
Alternativou pro ruční posouzení třmínky vyztuženého čtvercového sloupu je použití přídavného modulu RF-CONCRETE Members v programu RFEM a provedení posouzení podle normy ACI 318-14 [1]. Addon stanoví nutnou výztuž pro zatížení působící na sloup. Dále program stanoví navrženou výztuž na základě zadaných osových zatížení na sloup s uvažováním vzdáleností výztuže požadovaných normou. Uživatel může v tabulce výsledků provést drobné úpravy navrženého uspořádání výztuže.
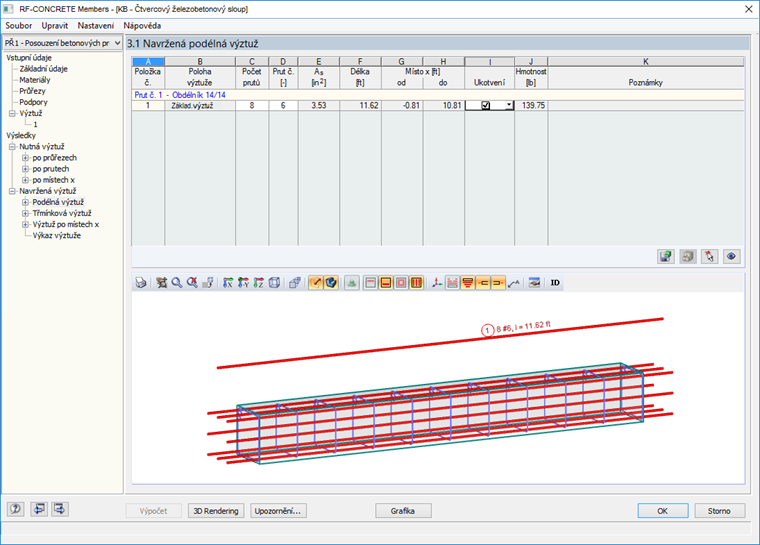
Pro působící zatížení v tomto příkladu určuje RF-CONCRETE Members požadovanou plochu výztuže prutu v podélném směru 1,92 in² a již existující plochu 3.53 in². Vypočítaná kotevní délka v přídavném modulu je 0,81 ft. Nesrovnalost ve srovnání s výše uvedenou kotevní délkou vypočítanou pomocí analytických rovnic je způsobena nelineárními výpočty programu s dílčím součinitelem γ. Součinitel γ je poměr mezi mezními a působícími vnitřními silami převzatými z programu RFEM. Kotevní délku v přídavném modulu RF-CONCRETE Members dostaneme vynásobením obrácené hodnoty gama délkou stanovenou z 25.4.9.2 [1]. Další informace k tomuto nelineárnímu výpočtu lze najít v níže uvedeném souboru nápovědy k modulu RF-CONCRETE Members. Tuto výztuž lze prohlédnout na obrázku 3.
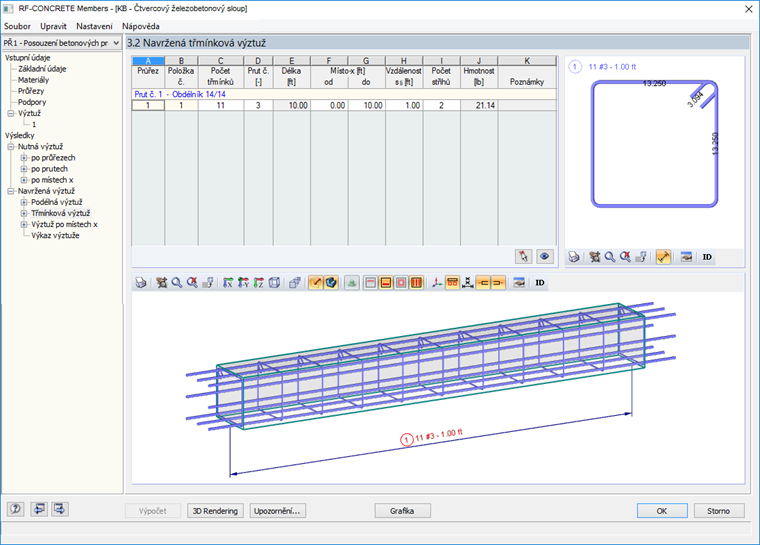
Navržená smyková výztuž pro prut v modulu RF-CONCRETE Members byla vypočítána na (11) č. 3 pruty s roztečí 12 in. Navržené uspořádání smykové výztuže je znázorněno na obrázku 4.
![Rozpětí podle obr. 5.2 z [1]](/cs/webimage/039540/3493372/01_Abmessungen_EN.png?mw=512&hash=3cc425f1463bd5981b358d5889e3109e07ae1233)
.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
