3473x

001388

Dipl.-Ing. (FH) Ulrich Lex

2017-01-04

Modeling of Point-Supported Glass Systems 1

The transparency of the glass material should not be missing in any building. In addition to the typical application areas such as windows, this building material is increasingly being used for facades, canopies, or even as bracing of stairways. Of course, the planning architects often set a very high standard of transparency on fixation of the glass panes. This requires special glass fittings that couple the glass panes.

Design Background

In addition to the general technical approvals of the individual producers, the design of point-supported fittings is regulated in DIN 18008 [1]. This German standard specifies two different ways:

Annex B – Verification / validation of finite element models
Annex C – Simplified method

In addition to the various design options, there are constructional provisions—especially for plate fittings—specifying the geometrical arrangement on a glass pane or the formation in the edge area.

Initial Data Used for Analysis

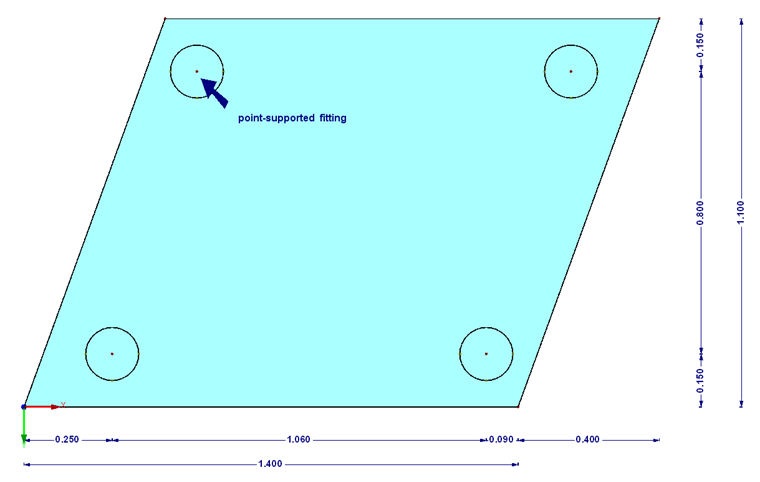
Laminated safety glass from heat-strengthened float glass 2 x 8 mm
Point fixing PH 793 by Glassline GmbH (approval Z-70.2-99 [3]), cylindrical head Ø 52 mm, drilling Ø 25 mm
Design load q_d = 4.5 kN/m²

System with Dimensions

Modeling in RFEM According to Simplified Method

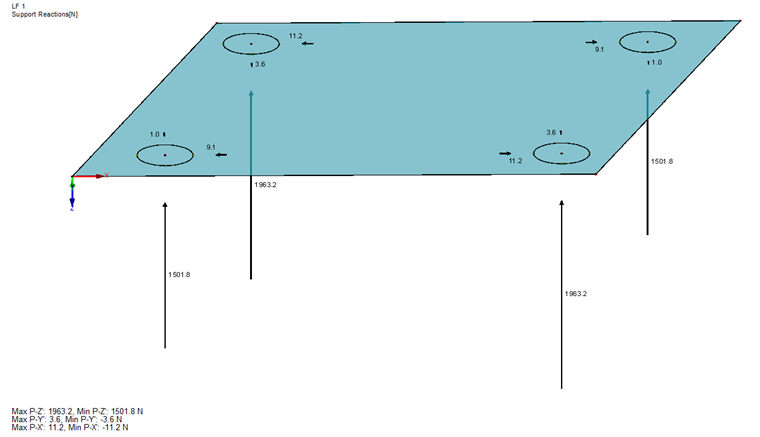
In the case of glass pane design according to the simplified method described in DIN 18008, Annex C [1], the pane may be analyzed without the drilling holes. The existing glass fittings are represented by springs. The existing spring stiffness is specified in the technical approval. In our example, it gives the following result:

C_Z,max = 1/24,372 + 1/3,015 = 2,683 N/mm
C_Z,min = 1/15,386 + 1/1,592 = 1,443 N/mm
C_Z,sel = 2,000 N/mm
C_V;x,y = 344 N/mm

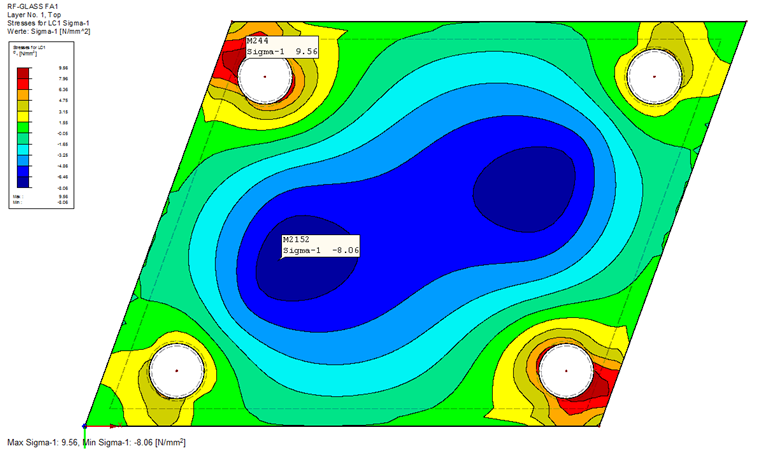
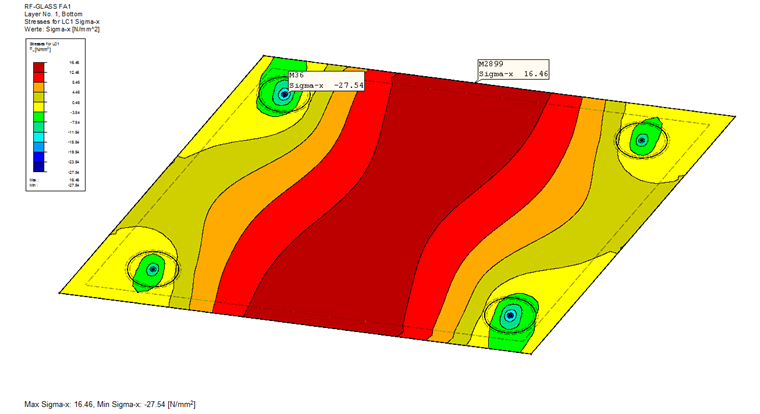
The following result values are calculated on the basis of the mentioned parameters.

Support Reactions - Local Results

Stresses - Local Results

All relevant stress ratios can now be calculated using the formulas and parameters provided by DIN 18008, Annex C [1].

Stress component F_Z:

σ_{Fz} = \frac{b_{Fz}}{d ²} \cdot \frac{t_{ref}^{2}}{t_{i}^{2}} \cdot F_{Z} \cdot δ_{Z} = \frac{15, 8}{25 ²} \cdot \frac{102}{82} \cdot 1.964 \cdot 0, 5 = 38, 8 N / mm ²

Formula 1

Stress component F_res:

\begin{array}{l} F_{res} = \sqrt{F_{x}^{2} F_{y}^{2}} = \sqrt{11 ² 4 ²} = 12 N \\ σ_{F, res} = \frac{b_{F, res}}{d ²} \cdot \frac{t_{ref}}{t_{i}} \cdot F_{res} \cdot δ_{F, res} = \frac{3, 92}{25 ²} \cdot \frac{10}{8} \cdot 12 \cdot 0, 5 = 0, 1 N / mm ² \end{array}

Formula 2

Stress component M_res:
Due to the hinged support around axes x, y, and z, there is no additional moment M_res.

Stress concentration in the drilling hole area:
σ_g = σ_g(3d) ∙ δ_g ∙ k = 9.6 ∙ 8 / 10.8 ∙ 1.6 = 11.4 N/mm²

The governing design stress value in the fitting area then results from the sum of the individual components.
E_d = 38.8 + 0.1 + 11.4 = 50.3 N/mm²

As the final step, the moment in the span must be considered. In this case, the moment has to be determined on a statically defined system.

Stress Analysis in Span Area

The governing stress in the span area is E_d = 16.5 N/mm².

The allowable stress for laminated safety glass is calculated as:

R_{d} = 1.1 \cdot \frac{f_{k, TVG}}{γ_{M}} = 1.1 \cdot \frac{70}{1.5} = 51.3 N / mm ²

Formula 3

Thus, it gives the result of the total design ratio of the glass η = 0.98.

In addition to the general stress analysis performed here, you can perform additional designs for the exact dimensions of the glass pane. For this, you can follow the standard.

Conclusion

Annex C of the German standard DIN 18008 provides very simple tools for designing point-supported glass fittings. By using the table values, you can very quickly estimate the structural behavior of the glass pane and determine the design ratio. Another option is specified in Annex B of the standard. This design method based on a finite element model will be explained in the next part of this article.

References

[1]	DIN 18008-3. (2013). Glass in Building – Design and Construction Rules – Part 3: Point Fixed Glazing, DIN 18008-3:2013-07.
[2]	Weller, B., Engelmann, M., Nicklisch, F., & Weimar, T. Glasbau-Praxis: Konstruktion und Bemessung Band 2: Beispiele nach DIN 18008, (3rd ed.). Berlin, Beuth.
[3]	DIBt. (2014). General Technical Approval Z-70.2-99. Berlin, September 4.

Author

Mr. Lex is responsible for developing products for glass structures and for quality assurance of the RFEM program. He also provides technical support for our customers.

Links

Structural Analysis and Design Software for Glass Structures

Downloads

RFEM Model File

8.12 MB

;