The model of this technical article is based on Example 5.5.3 in the technical literature [1]. It explains the effects of the connection stiffness on the determination of internal forces, as well as the design of connections using the example of a two-story, double-spanned steel frame.
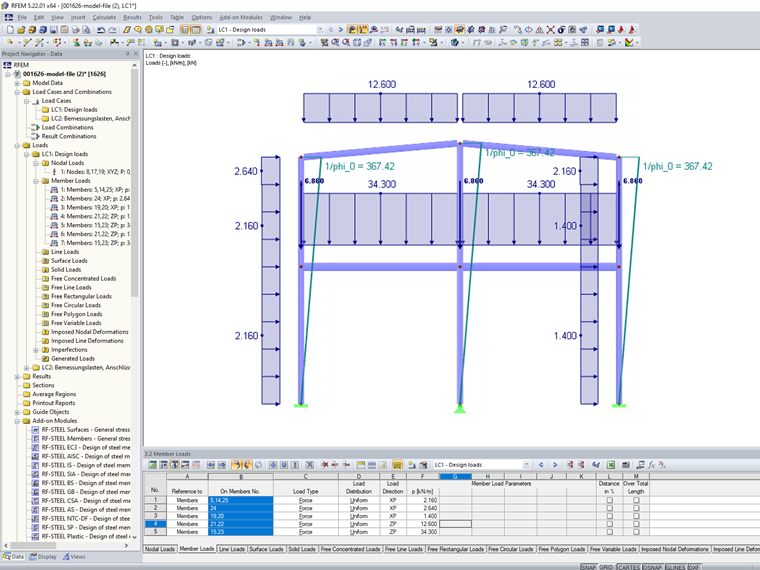
Loading
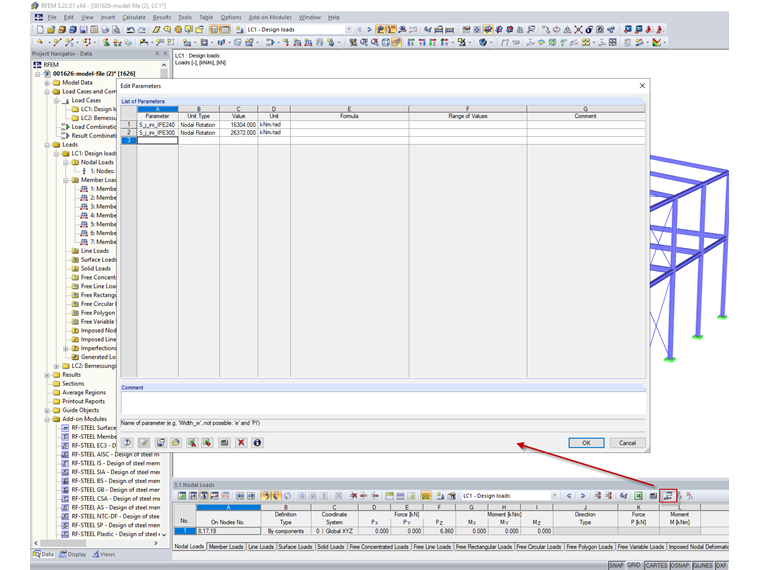
Loads resulting from a feed width of four meters are applied according to [1]. Only the displacement of the member hinges by 0.1 m from the axis of the columns is omitted. The global initial inclinations are calculated according to Equation 5.5 in [2]:
where
to
Geometry of Connections and Moment-Rotation Characteristics
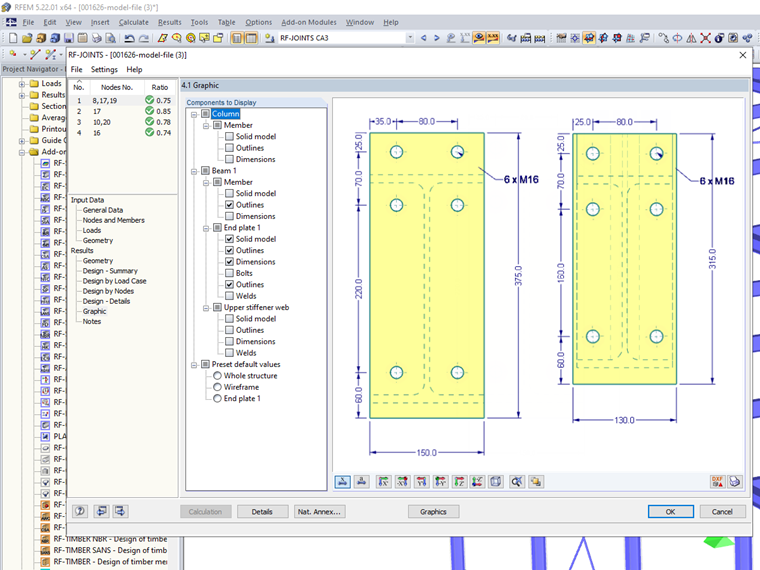
The connections of the beams in the intermediate ceiling as well as in the roof are formed with extended end plates without stiffeners in the columns. This design leads to economical advantages in the current case.
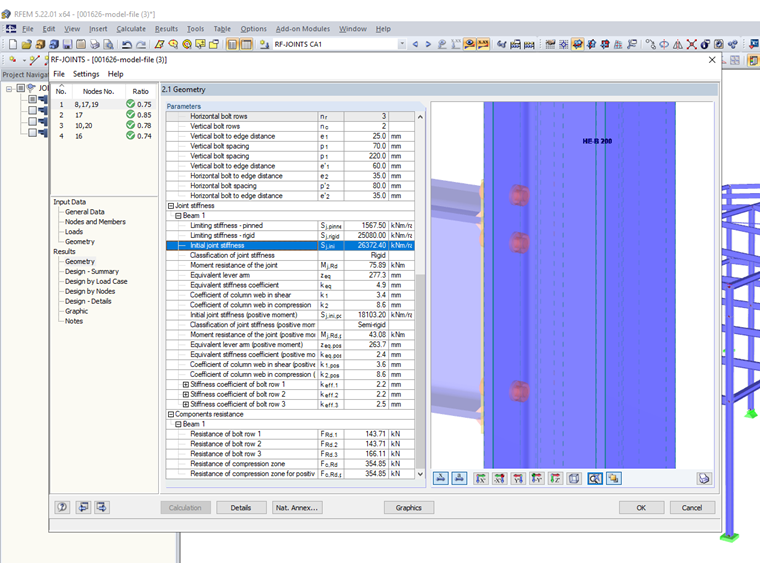
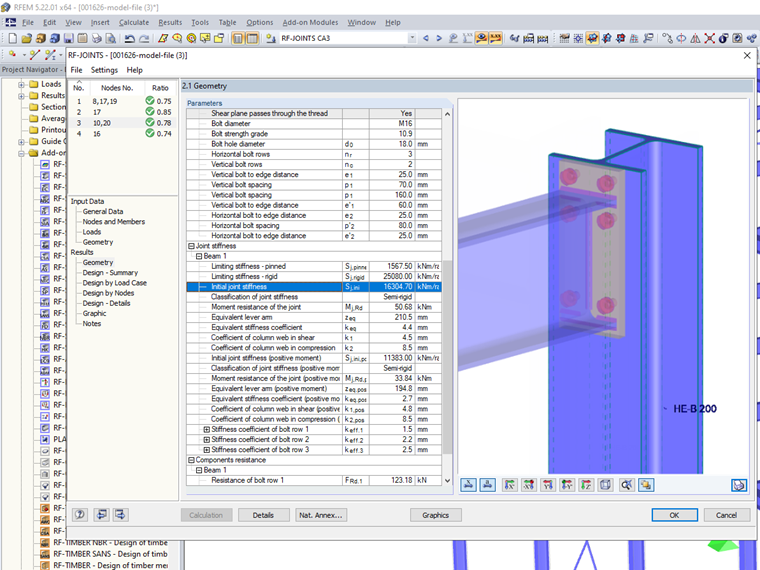
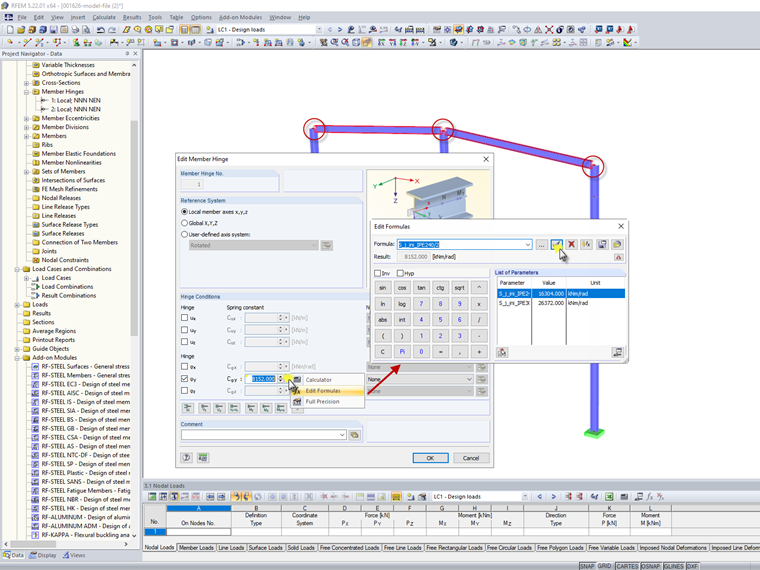
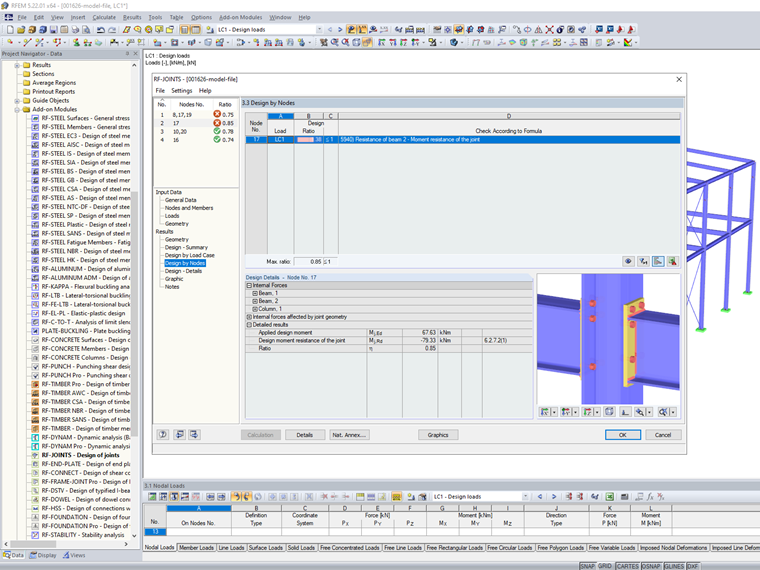
According to [1], the effect of the moment-rotation characteristics of the connections on the distribution of internal forces in a structure for deformable connections usually has to be taken into account. With the component method specified in EN 1993-1-8, it is possible to calculate the initial elastic stiffness Sj,ini for the connections. The RF-/JOINTS Steel Rigid add-on module is utilized here.
The application of the torsional spring stiffness in the model is simplified according to EN 1993-1-8 Section 5.1.2 (4) and is defined for quick adjustment in the system in the case of changes by means of parametrization.
IPE 240: Sj,Model = Sj,ini / η = 16,304 / 2 = 8,152 kNm/rad
IPE 300: Sj,Model = Sj,ini / η = 26,372 / 2 = 13,186 kNm/rad
Internal Forces and Connection Design
The determination of the first mode shape in the frame plane with the RSBUCK or RF-STABILITY add-on modules results in a critical load factor acr of 12.6. Thus, it is possible to calculate the internal forces according to Equation 5.1 in [2] according to the linear static analysis.
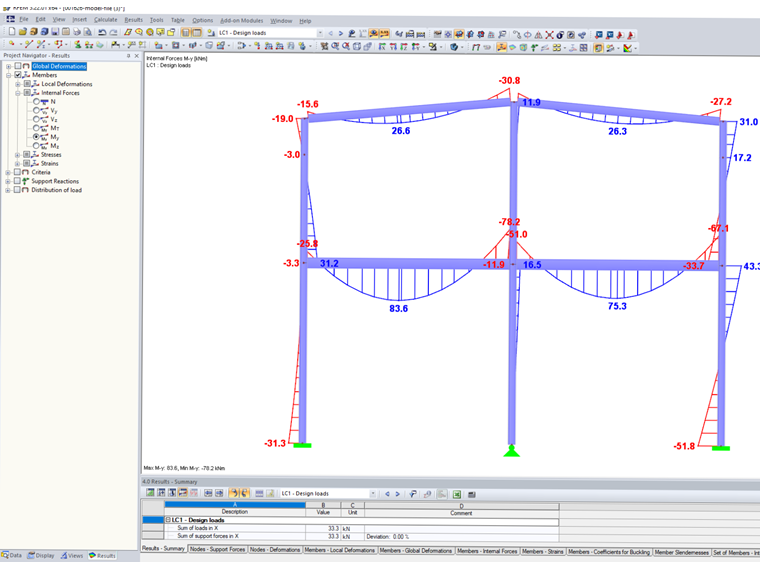
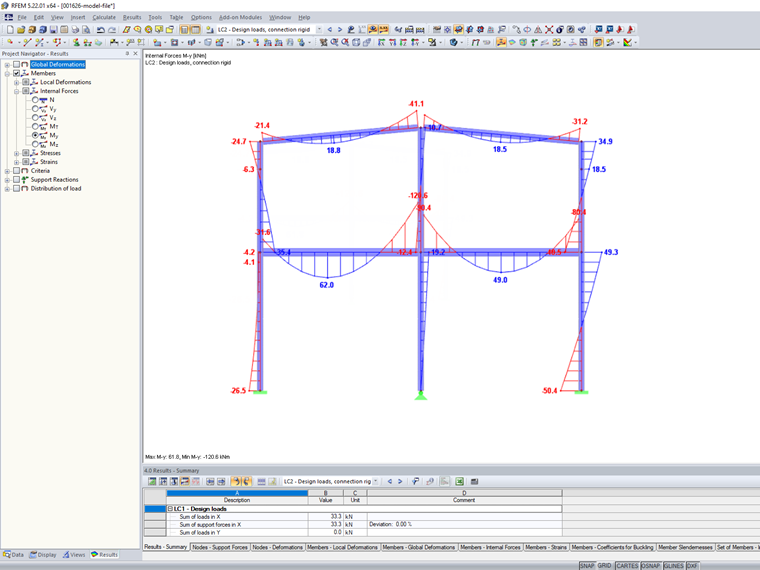
The calculation of the load case with rigidly modeled member hinges results in the following internal forces.
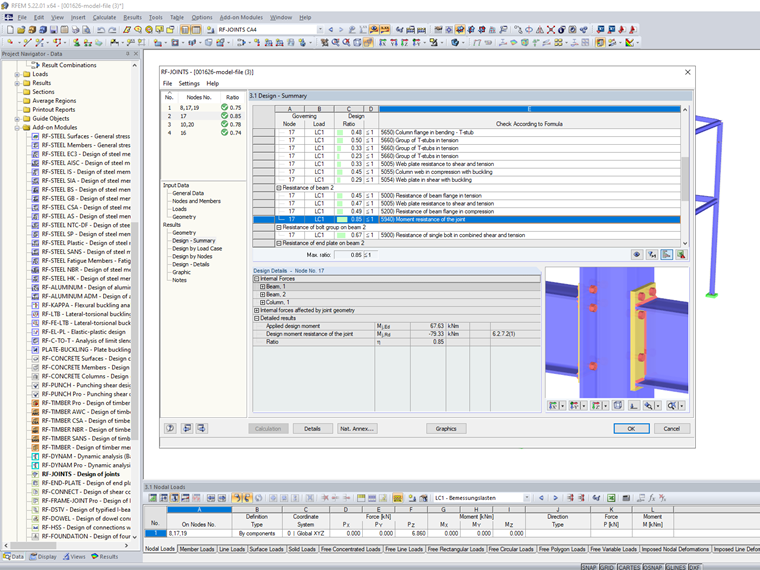
Based on these internal forces, the connection is designed according to EN 1993-1-8 in the RF-/JOINTS Steel Rigid add-on module.
The calculation of the load case with rigid member hinges results in the following internal forces.
With these higher internal forces at the connections between the beam and the column, it is no longer possible to design the connections.
Conclusion
Considering the connection stiffness in the structural analysis allows for the unreinforced design of the connections as well as a more homogeneous utilization of the beams in the present two-story, double-spanned steel frame in steel skeleton construction.