In the RF-/STEEL EC 3 add-on module, you can use the RF-/STEEL Cold-Formed Sections extension to perform an analysis of local transverse forces for non-stiffened webs according to [1], 6.1.7 (the module extension requires a separate license). This article shows the corresponding design methods using the example of a bending beam made of a cold-formed C-section and subjected to a single load.
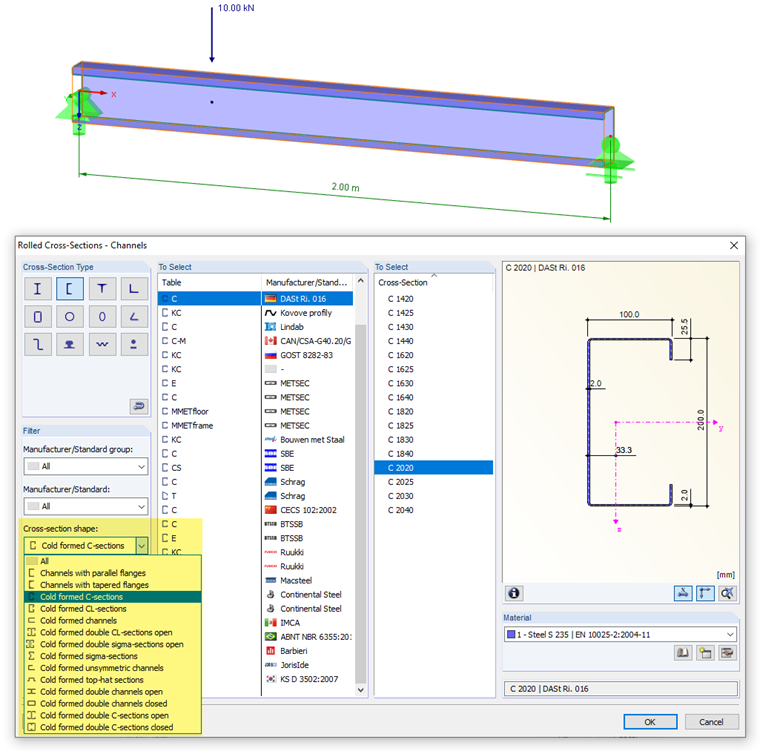
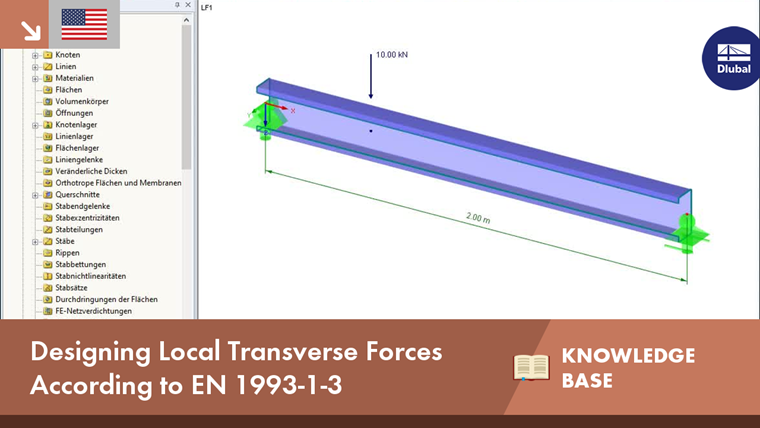
System and Loading
A beam with a length of two meters consists of a C 2020 cold-formed section made of S 235 steel. It is loaded with a single load of 10 kN at a distance of 50 cm from the support. The load acts at the shear center. The self-weight is not taken into account.
When selecting the cross-section from the library, please note that the cross-section shape of the C-section corresponds to the "Cold-Formed C-Sections" category. This condition can be set using the filter function. The RF-/STEEL Cold-Formed Sections module extension is made for the design of cold-formed sections: A rolled C-section or channel section would not be designed according to [1].
Entering Data in RF-/STEEL Cold-Formed Sections
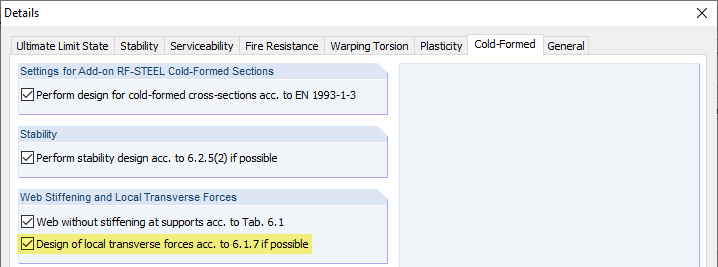
In the RF-/STEEL EC 3 add-on module, the specifications for a design according to EN 1993-1-3 [1] must be made in the "Cold-Formed Sections" tab of the "Details" dialog box.
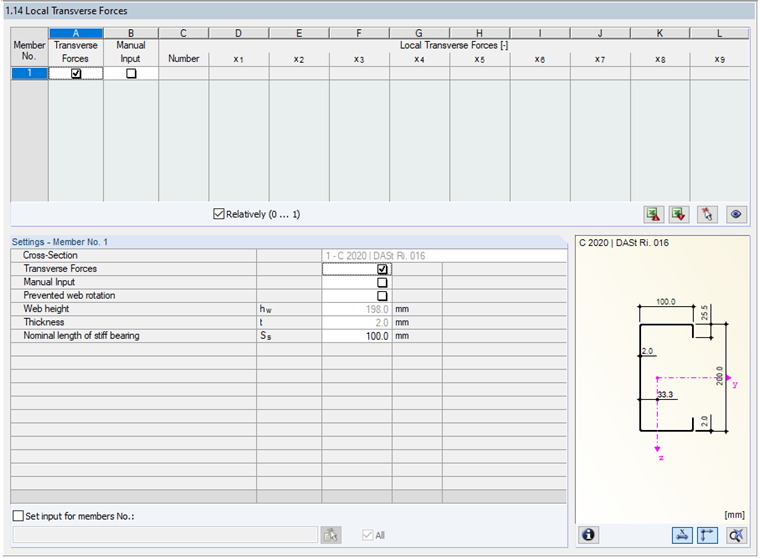
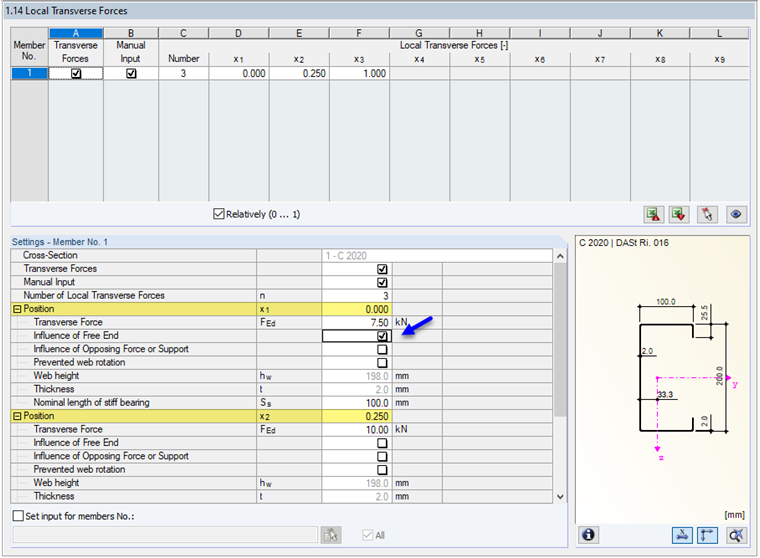
The "Design of local transverse forces according to 6.1.7 if possible" check box controls whether the program checks local failure modes in the web. If this option is activated, it is possible to define the boundary conditions such as the length of the stiff bearing in Window "1.14 Local Transverse Forces".
The consideration of the transverse forces is activated by default. Thus, the shear force distribution is used for the design of the web loading for local load application. The program analyzes the locations of discontinuity resulting from the shear force distribution. The "Nominal length of stiff bearing" is preset to 0.10 m.
Results in RF-/STEEL EC3
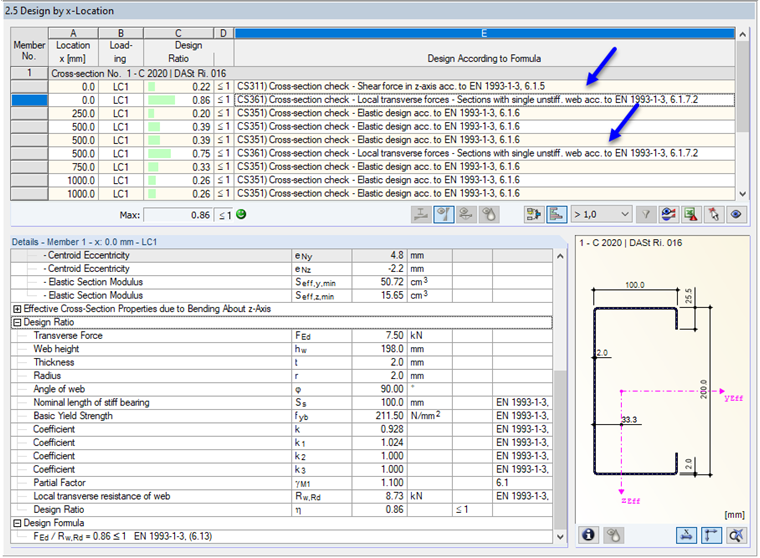
There are, at most, two steps to calculate the effective cross-section iteratively. Then, the design ratios due to local transverse forces are displayed in the design checks. The details of each design can be viewed as "intermediate values".
According to the shear force distribution, the local transverse force design is performed at both supports and the location of the local load application. Location x = 0.00 m has the maximum design ratio. The location design is as follows:
We have a support reaction on one cross-section that has only one web. The C-section with a plate thickness of t = 2.0 mm has stiffened belts because of its lips. The distance of the support from the free end is 0.00 m, which is less than 1.5 times the web height hw = 198 mm. Thus, [1], Equation (6.15a) governs for determining the web resistance Rw,Rd.
You have to apply the following parameters:
This results in the following web resistance:
The design condition according to [1], Equation (6.13) is fulfilled:
The design is the same for the remaining two design locations.
Option: Defining Forces Manually
If the shear force distribution does not represent the introduced load realistically, the locations of the load and the load magnitudes, including the nominal lengths of the stiff bearing, can be defined manually. You can see this in the attached RFEM model in Design Case 2.
In the case of a manually defined force, there is no automatic comparison of the shear force effect for the support points. You have to define these locations individually with the respective support forces. To do this, select the "Free End" check box as shown in Image 05. Only then is the distance c ≤ 1.5 hw taken into account, and [1], Equation (6.15a) is used for the design. Otherwise, [1], Equation (6.15d) would apply.
Conclusion
With the RF-/STEEL Cold-Formed Sections module extension for RF-/STEEL EC3, it is possible to perform, among other things, design checks for local transverse forces according to [1], Section 6.1.7. The locations relevant for the design are determined automatically from the shear force distribution. Alternatively, you can specify the forces manually. The design for local transverse forces with RF-/STEEL Cold-Formed Sections is performed according to [1], 6.1.7.2 for cross-sections with an unstiffened web or according to [1], 6.1.7.3 for cross-sections with two or more webs without stiffening. Web cross-sections with longitudinal stiffeners cannot be designed according to [1], 6.1.7.4.