Theoretical Application
Axial compression applies if it is assumed that second-order effects (imperfections, asymmetry, and so on) can be neglected while respecting in particular the slenderness criterion, which depends on various parameters (slenderness coefficient, limiting slenderness, effective length).
Then, under the single loading of a normal force NEd, the force that can be balanced by the concrete cross-section corresponds to its maximum load-bearing capacity for compression, which depends directly on its section and its design resistance. The reinforcement will balance the rest of the axial compressive load.
Theory Application with RF-CONCRETE Columns Add-on Module
In this article, we will analyze the results obtained automatically for the reinforcement calculation.
The parameters remain the same and are listed below:
- Permanent loads: Ng = 1,390 kN
- Variable loads: Nq = 1,000 kN
- Column length: l = 2.1 m
- Rectangular cross-section: width b = 40 cm / height h = 45 cm
- Column's self-weight: negligible
- Column not integrated into bracing
- Concrete strength class: C25/30
- Steel: S 500 A for inclined graph
- Diameter of longitudinal reinforcement: ϕ = 20 mm
- Diameter of transverse reinforcement: ϕt = 8 mm
- Concrete cover: 3 cm
Real Cross-Section to Be Calculated
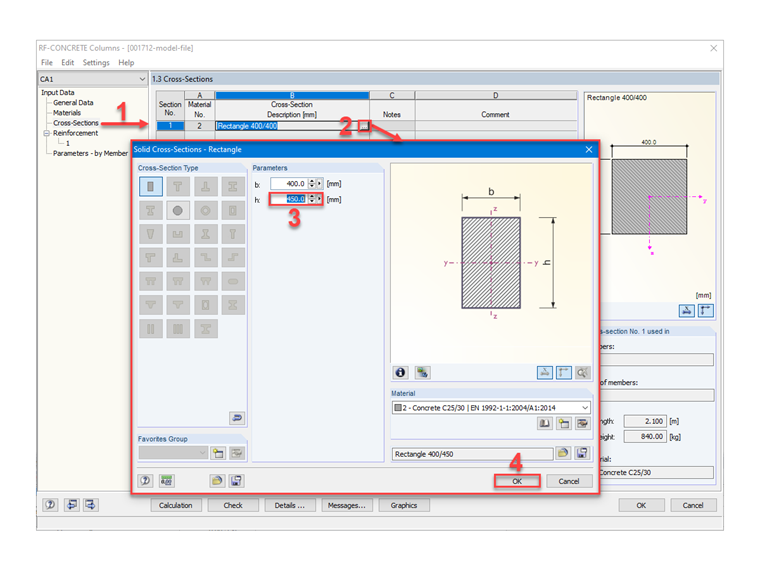
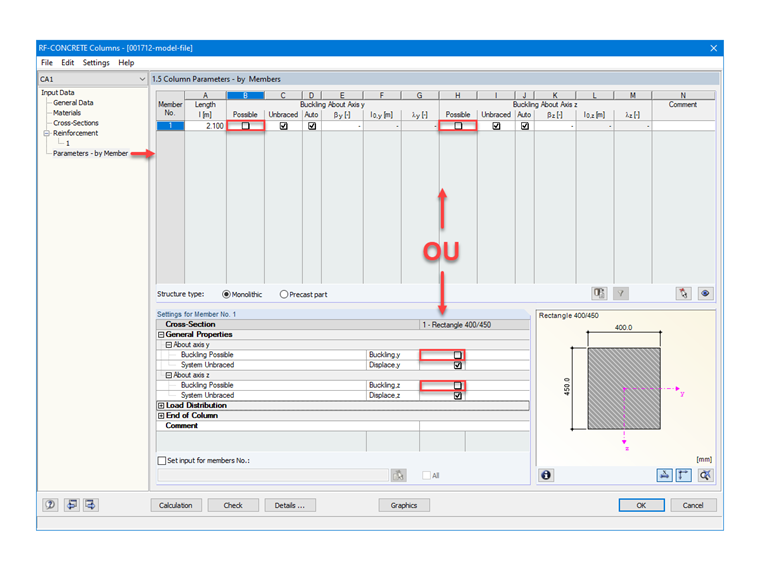
Since it is impossible in RF‑CONCRETE Columns to optimize the cross-section height, the section's real height h is directly modified and set to 45 cm.
Image 02 shows the steps to change the height of the rectangular cross-section in RF‑CONCRETE Columns.
Material Properties
The formulas for the materials' strength and strain are described in detail in the technical article mentioned above.
Total area of pure concrete section
Ac = b ⋅ h = 0.40 ⋅ 0.45 = 0.18 m²
Design value of the compressive strength of concrete
fcd = 16.7 MPa
Relative compression strain for maximum stress
εc2 = 2‰
Design yield strength of reinforcing steel
fyd= 435 MPa
Limit strain in reinforcement
εud = 2.17‰
Stress in reinforcement
σs = 400 MPa
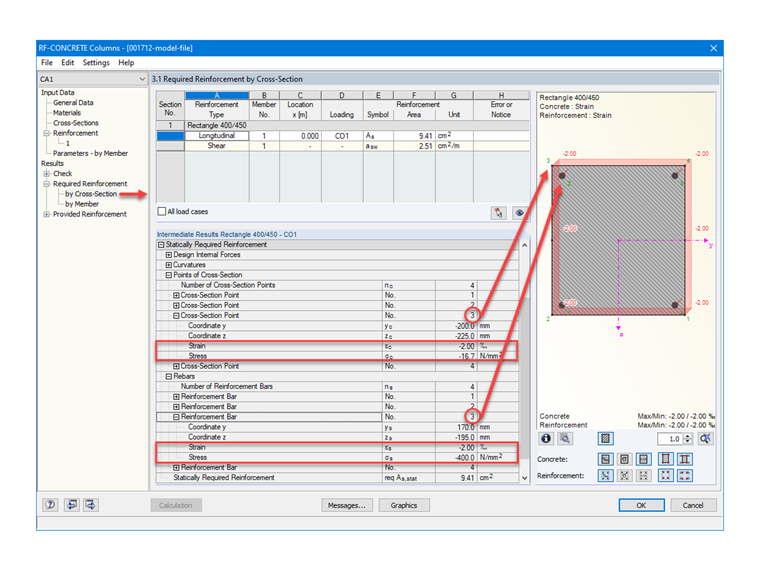
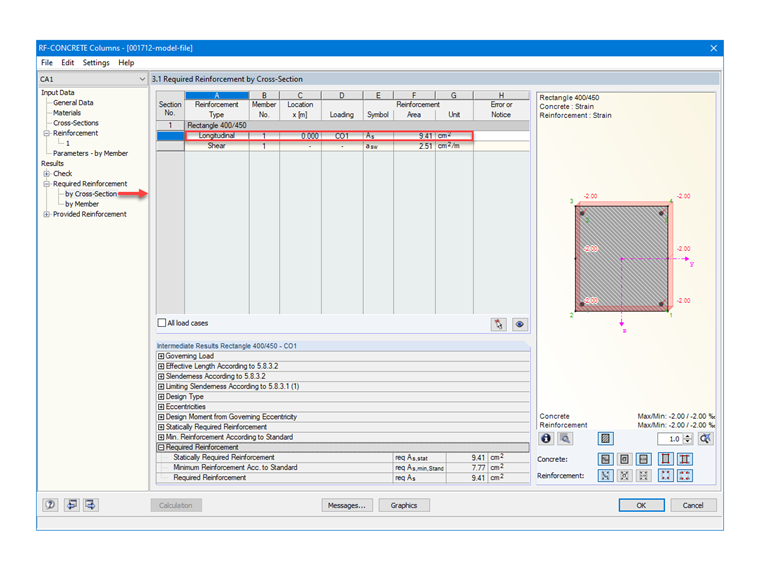
In order to verify the material settings in RF‑CONCRETE Columns, Image 03 shows the expected stresses and strains for the concrete and the required reinforcement.
Ultimate Limit State
Ultimate limit state design loads
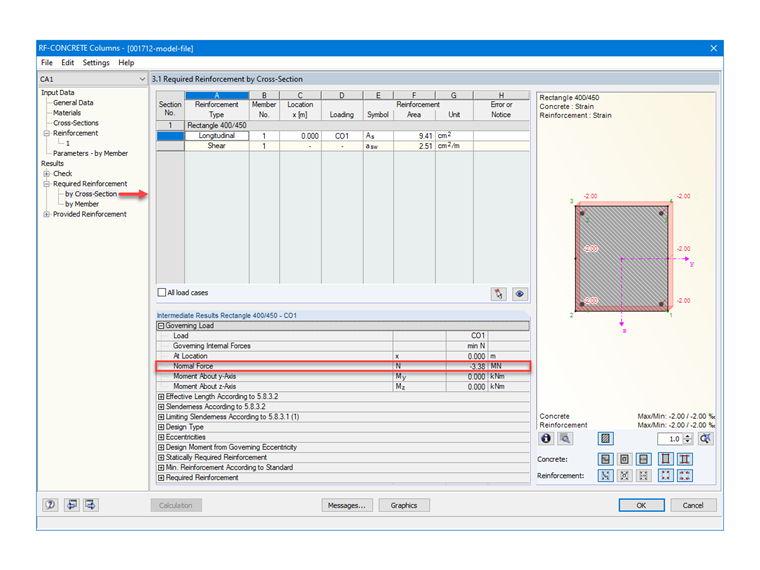
NEd = 1.35 ⋅ Ng + 1.5 ⋅ Nq
NEd = 1.35 ⋅ 1390 + 1.5 ⋅ 1000 = 3.38 MN
NEd ... Design value of acting axial force
Second-Order Effects Not Taken into Account in ULS
As the model is identical for this article and the one that serves as a basis for comparison, we have modeled the same column restrained at the base and free at the head to be able to apply the load correctly at the column head. However, we consider that the column is still fixed at the head to some beams. For this, we have applied an effective length factor to the column, which allows for modifying the column's slenderness value.
Effective length factor according to EN 1992-1-1 - 5.8.3.2 (3) - Formula 5.15
kcr = 0.59
Slenderness according to EN 1992-1-1 - 5.8.3.2 (1) - Formula 5.14
λz = 10.73 m
Limiting slenderness according to EN 1992-1-1 - 5.8.3.1 (1) - Formula 5.13N
n = 1.125
λlim = 20 ⋅ 07. ⋅ 1.1 ⋅ 0.7 / √1.125 = 10.16 m
λz > λlim → The condition is not fulfilled.
However, we are still going to calculate in simple compression because, the difference being small, we will see later that with the mechanical ratio of the reinforcements, the condition will be respected. For this, Image 05 describes how to deactivate the possibility of having buckling around each axis of the cross-section in RF‑CONCRETE Columns.
Load-Bearing Cross-Section
Equilibrium force of concrete
Fc = Ac ⋅ fcd = 0.40 ⋅ 0.45 ⋅ 16.7 = 3 MN
Equilibrium force of reinforcement
Fs = NEd - Fc = 3.38 - 3 = 0.38 MN
We deduce the corresponding reinforcement area:
Reinforcement area
As = Fs / σs = 0.38 / 400 ⋅ 104 = 9.5 cm²
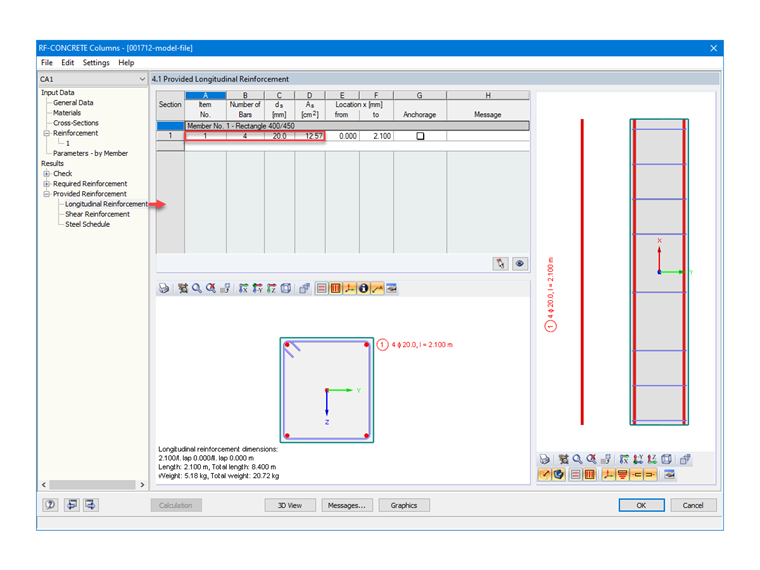
Having configured steels with a diameter of 20 mm in RF‑CONCRETE Columns, the reinforcements provided and determined automatically by the module are 4 members, with a distribution in the corners, as requested; that is, 1 HA 20 per corner. Therefore, the result of the cross-sectional area of reinforcement is as follows:
As = 4 ⋅ 3.142 = 12.57 cm²
Mechanical reinforcement ratio
ω = (As ⋅ fyd) / (Ac ⋅ fcd) = 0.182
Final check of limiting slenderness
λlim = (20 ⋅ 0.7 ⋅ √(1 + 2 ⋅ 0.182) ⋅ 0.7) / √1.125 = 10.79 m
λz < λlim → The slenderness criterion is fulfilled.