Teoretické použití
O namáhání v osovém tlaku se jedná, pokud lze zanedbat účinky druhého řádu (imperfekce, asymetrie atd.), přičemž je třeba uvážit štíhlostní kritérium, které závisí na různých parametrech (štíhlostní poměr, mezní štíhlost, účinná délka).
Při namáhání v prostém tlaku Ned tak síla, kterou může vyvažovat betonový průřez, odpovídá jeho maximální únosnosti v tlaku, která přímo závisí na jeho průřezu a návrhové pevnosti. Výztuž pak vyvažuje zbytek zatížení v osovém tlaku.
Uplatnění teorie pomocí přídavného modulu RF-CONCRETE Columns
Nyní přistoupíme k analýze výsledků, které jsme automaticky obdrželi při výpočtu výztuže.
Parametry zůstávají stejné, uvádíme je znovu níže:
- Stálá zatížení: Ng = 1390 kN
- Proměnná zatížení: Nq = 1 000 kN
- Délka sloupu: l = 2,1 m
- Obdélníkový průřez: šířka b = 40 cm / výška h = 45 cm
- Vlastní tíha sloupu: zanedbatelná
- Sloup není součástí ztužení
- Třída pevnosti betonu: C25/30
- Ocel: S 500 A se stoupající větví
- Průměr podélné výztuže: ϕ = 20 mm
- Průměr příčné výztuže: ϕt = 8 mm
- Krycí betonová vrstva: 3 cm
Skutečný průřez pro výpočet
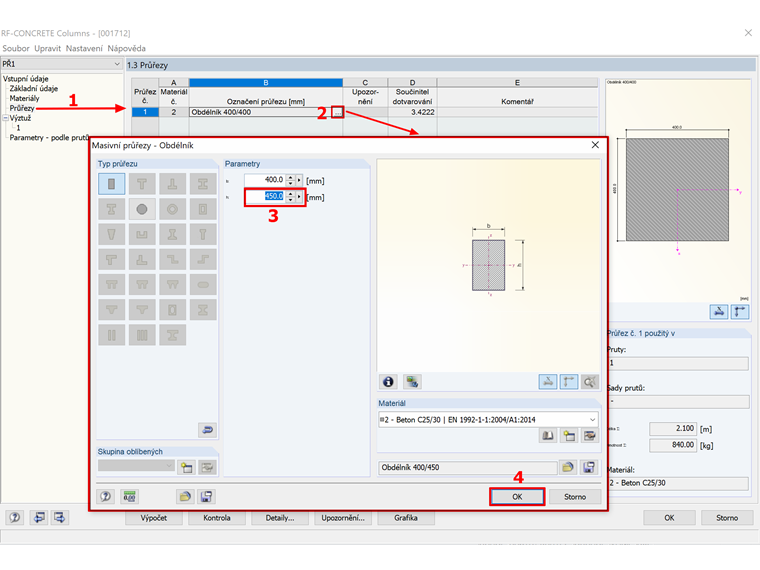
Protože v přídavném modulu RF-CONCRETE Columns nelze optimalizovat výšku průřezu, upravíme skutečnou výšku průřezu h přímo na 45 cm.
Na obr. 02 vidíme kroky pro úpravu výšky obdélníkového průřezu v modulu RF-CONCRETE Columns.
Materiálové charakteristiky
Vzorce pro stanovení pevnosti a přetvoření materiálů uvádíme podrobně ve výše zmíněném příspěvku.
Celková plocha betonového průřezu
Ac = b ⋅ h = 0,40 ⋅ 0,45 = 0,18 m²
Návrhová hodnota pevnosti betonu v tlaku
fcd = 16,7 MPa
Poměrné přetvoření v tlaku při maximálním napětí
εc2 = 2 ‰
Návrhová mez kluzu betonářské oceli
fyd= 435 MPa
Mezní přetvoření ve výztuži
εud = 2,17 ‰
Napětí ve výztuži
σs = 400 MPa
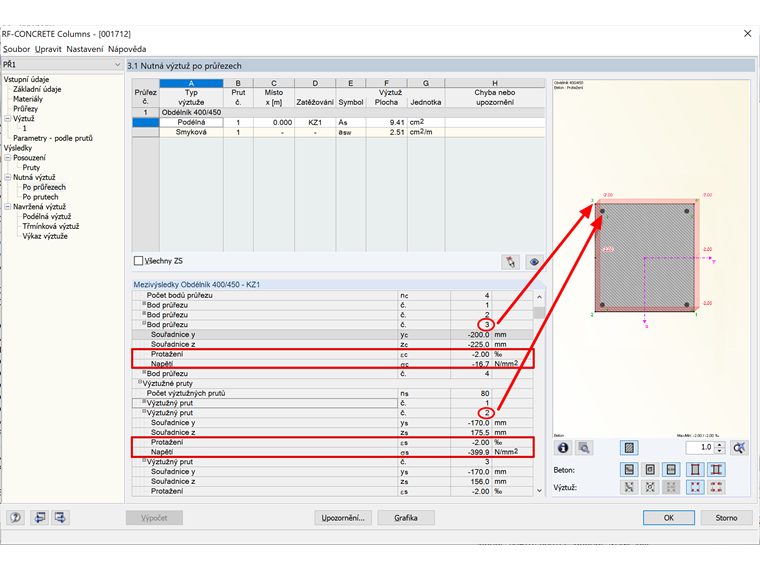
Pro kontrolu nastavení materiálu v modulu RF-CONCRETE Columns jsou na obr. 03 znázorněna návrhová napětí a přetvoření u betonu a nutné výztuže.
Mezní stav únosnosti
Namáhání v mezním stavu únosnosti
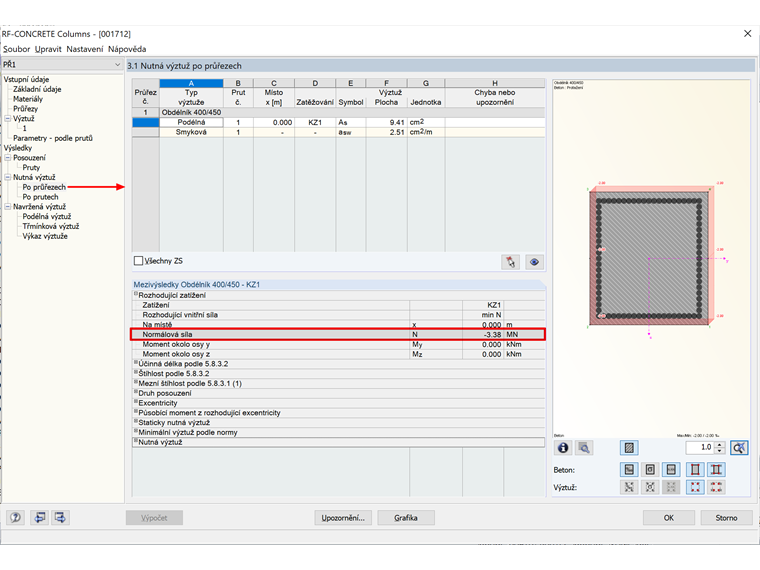
NEd = 1,35 ⋅ Ng + 1,5 ⋅ Nq
NEd = 1,35 ⋅ 1390 + 1,5 ⋅ 1000 = 3,38 MN
NEd ... Návrhová hodnota působící normálové síly
Účinky druhého řádu se v MSÚ nezohledňují.
Protože model se u tohoto článku shoduje s modelem z příspěvku, který nám slouží jako základ pro porovnání, namodelovali jsme stejný sloup vetknutý v patě a volný v hlavě, abychom mohli správně zohlednit zatížení v hlavě sloupu. Vycházíme nicméně z toho, že sloup je v hlavě připevněn k nosníkům. U sloupu tak uvažujeme součinitel vzpěrné délky, který umožňuje upravit štíhlost sloupu.
Součinitel vzpěrné délky podle EN 1992-1-1 - 5.8.3.2 (3) - rovnice 5.15
kcr = 0,59
Štíhlost podle EN 1992-1-1 - 5.8.3.2 (1) - rovnice 5.14
λz = 10,73 m
Mezní štíhlost podle EN 1992-1-1 - 5.8.3.1 (1) - rovnice 5.13N
n = 1,125
λlim = 20 ⋅ 0,7 ⋅ 1,1 ⋅ 0,7 / √1,125 = 10,16 m
λz > λlim → Podmínka není splněna.
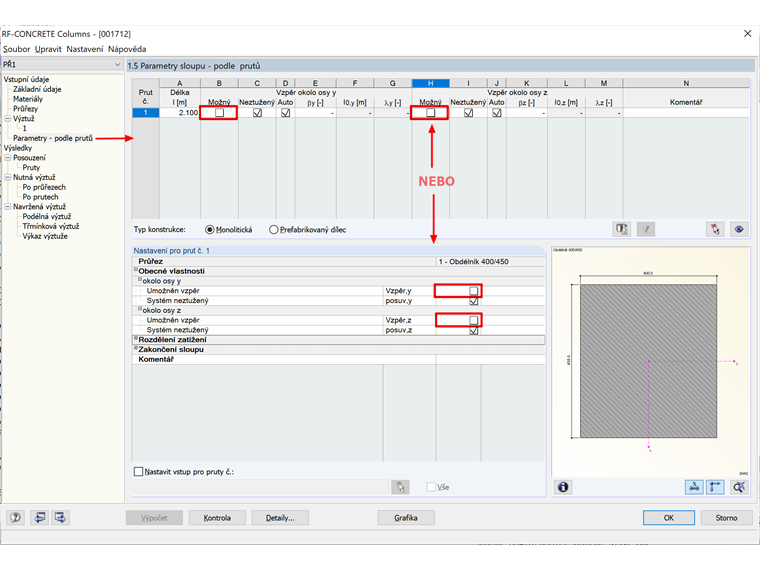
Nicméně budeme přesto počítat s prostým tlakem, protože s ohledem na malou odchylku zjistíme dále, že s mechanickým stupněm vyztužení bude podmínka splněna. Na obr. 05 ukazujeme, jak lze v modulu RF-CONCRETE Columns deaktivovat možnost vybočení okolo každé osy průřezu.
Zatížený průřez
Vyrovnávací síla betonu
Fc = Ac ⋅ fcd = 0,40 ⋅ 0,45 ⋅ 16,7 = 3 MN
Vyrovnávací síla výztuže
Fs = NEd - Fc = 3,38 - 3 = 0,38 MN
Odvodíme příslušný průřez výztuže:
Průřezová plocha výztuže
As = Fs / σs = 0,38 / 400 ⋅ 104 = 9,5 cm²
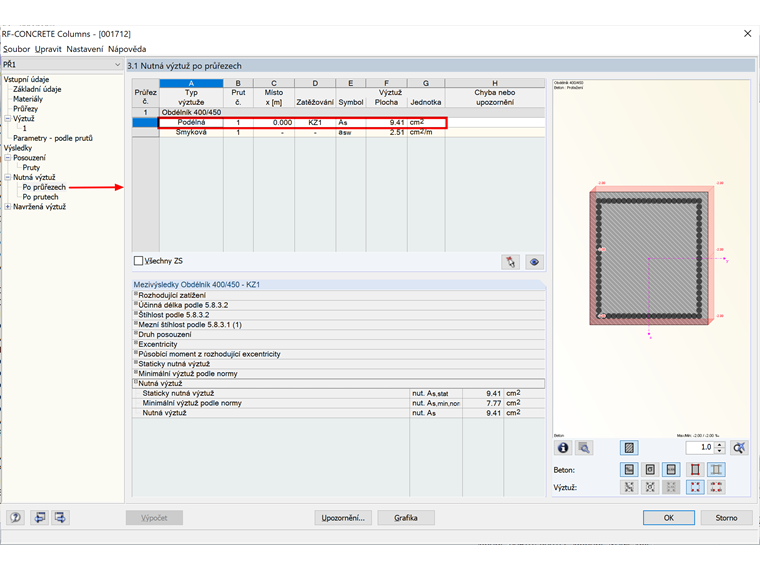
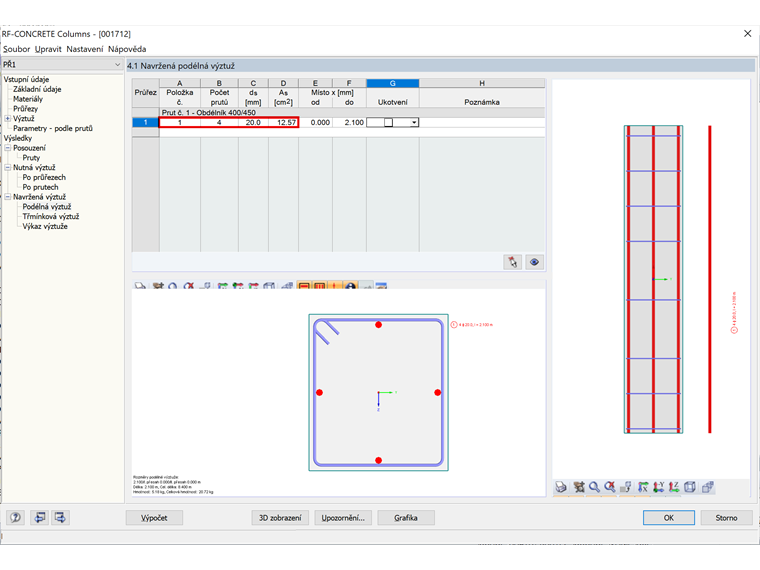
Protože jsme v modulu RF-CONCRETE Columns nastavili betonářskou výztuž o průměru 20 mm, stanoví modul automaticky 4 pruty návrhové výztuže s rozmístěním v rozích, tj. 1 HA 20 na roh. Výsledkem je tedy průřezová plocha výztuže následující:
As = 4 ⋅ 3,142 = 12,57 cm²
Mechanický stupeň vyztužení
ω = (As ⋅ fyd) / (Ac ⋅ fcd) = 0,182
Závěrečná kontrola mezní štíhlosti
λlim = (20 ⋅ 0,7 ⋅ √(1 + 2 ⋅ 0,182) ⋅ 0,7) / √1,125 = 10,79 m
λz < λlim → Štíhlostní kritérium je splněno.