323x

001972

Hedi Boukraa, B.Sc.

2025-08-07

Required Reinforcement in Bucket with Rough Inner Walls: Design Approach and Steps

The article describes the complete derivation and design of the required bucket reinforcement. Both horizontal and vertical stirrups are analyzed.

The designed foundation is a bucket foundation with rough bucket sides. The connected column has a rectangular cross-section with dimensions of 30 cm × 40 cm. The design is based on DIN EN 1992-1-1. The materials used are concrete with the strength class C 35/45 and reinforcing steel of the type B500S(A). The concrete cover complies with the minimum requirements of the standard, designed for exposure classes XC3 for construction on prepared ground.

Dimensions of Foundation Slab and Bucket

All dimensions are specified in the Geometry tab. The slab has a width of 3.30 m, a length of 2.60 m, and a thickness of 0.36 m. The bucket has a height of 1.31 m; the embedment depth of the column is also 1.31 m. The eccentricity of the column in the x-direction is −0.30 m, related to the center of the foundation plate.

Geometric details of a foundation plate with bucket, focusing on technical aspects of the structure.

Foundation Slab and Bucket Geometry

Top view of bucket foundation shows detailed dimensions for structural design.

Top View of Bucket Foundation with Dimensions

There are two options for arranging the horizontal stirrups in the bucket:

Stirrups that enclose the column
Stirrups that lie completely within a bucket wall

Enclosing stirrups are used in this example. The ‘’'Reinforcement'‘’ tab includes the specifications on the reinforcing steel material, the reinforcement type of the slab, and the arrangement type of the horizontal stirrups in the bucket.

Detailed view of reinforcement settings for a bucket foundation in a CAD software interface.

Bucket Foundation | Tab Reinforcement

Load Cases

The internal forces of the following load cases are available for the ultimate limit state design:

Load Case	P_Z,d [kN]	P_X,d [kN]	P_Y,d [kN]	M_X,d [kNm]	M_Y,d [kNm]
1	300	-50	20	100	250
2	100	0	0	0	327
3	500	0	0	150	-150

Required Bucket Reinforcement

Required Outer Horizontal Reinforcement

Load Combination 1 (LC1+LC2) results in the largest required reinforcement area of the horizontal outer stirrups in the bucket and is thus governing. The horizontal forces on the bucket walls are as follows:

H_{t, x} = \frac{6}{5} \cdot \frac{M_{y}}{d} + \frac{6}{5} \cdot H_{x} = \frac{6}{5} \cdot \frac{250 kNm}{1, 310 m} + \frac{6}{5} \cdot 50 kN = 289.01 kN

H_{t, y} = \frac{6}{5} \cdot \frac{M_{y}}{d} + \frac{6}{5} \cdot H_{x} = \frac{6}{5} \cdot \frac{250 kNm}{1, 310 m} + \frac{6}{5} \cdot 50 kN = 289.01 kN

Horizontal Forces on Bucket Walls from Load Combination 1

This stirrup is subjected to tension due to two different actions: On one hand, a tensile force arises from the bending of the bucket wall, which is perpendicular to the considered horizontal force. On the other hand, a tensile force acts through the direct tensile stress of the wall, aligned parallel to the considered horizontal force.

From the horizontal force H_t,x, two tensile forces in the outer stirrups result:

In the wall in the x-direction, the tensile force T_H,x arises from tensile stress.
In the wall in the y-direction, the tensile force T_{H,out,x(Wall)} results from bending of this orthogonal wall.

Similarly, from the horizontal force H_t,y:

In the wall in the y-direction, the tensile force T_H,y arises from tensile stress.
In the wall in the x-direction, the tensile force T_{H,out,y(Wall)} results from bending of this orthogonal wall.

Tensile Forces in Outer Stirrups

For determining the maximum tensile force in the stirrup, you need to add the effects of both bending and tension. This is necessary, because their causes – that is, simultaneously acting horizontal components (H_t,x and H_t,y) – originate from the same load case and are thus effective simultaneously.

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tension in x-Direction

The upper horizontal force H_t,x can be divided in such a way that each half acts at the quarter points of the column's length in the y-direction.

Detailed view of the internal moments in a structural model with different load configurations.

Determination of Internal Moment

The proportional tensile force in the outer stirrups is then:

T_{h, x} = \frac{|H_{t, x}|}{4}

Proportional Tension Force T_h,x

Thus, the required reinforcement area of the horizontal stirrups in the bucket due to the tensile force in the x-direction is:

A_{sw, h, \erf} (H_{t, x}) = \frac{T_{h, x}}{f_{yd}} = \frac{72.25 kN}{43, . 47 kN / {cm}^{2}}

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tensile Force in x-Direction

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tension in y-Direction

The required reinforcement area of the horizontal stirrups in the bucket due to the tensile force in y-direction H_t,y is determined similarly as H_t,x:

T_{h, y} = \frac{|H_{t, y}|}{4} = \frac{|115.60 kN|}{4} = 28.90 kN

A_{sw, h, req} (H_{t, y}) = \frac{T_{h, y}}{f_{yd}} = \frac{28.90 kN}{43.47 kN / cm ²}

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tensile Force in y-Direction

Required Reinforcement Area of Outer Horizontal Stirrups in Bucket Due to Bending of H_t,x

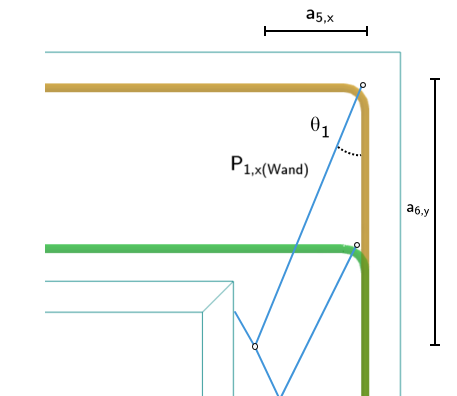
Considering the upper right corner alone (see the image above), it must be in force equilibrium. The horizontal inner forces must be balanced with the outer, loading horizontal force. Since no vertical outer forces act in the section considered here, it is now necessary to find a moment equilibrium. First, the sum of the moments about the point P is calculated. For this, the lever arms are determined:

a_{2, y} = \frac{c_{y}}{4} = \frac{0.30 m}{4} = 0.08 m

a_{3, y} = \frac{c_{y}}{2} + a_{ty} + c_{(k)} + \frac{d_{s, h}}{2} = \frac{0.30 m}{2} + 0.10 m + 0.05 m + \frac{0, 014 m}{2} = 0.31 m

a_{4, y} = \frac{d_{b, y}}{2} - c_{(k)} - \frac{d_{s, h}}{2} = \frac{1.24 m}{2} - 0.05 m - \frac{0, 014 m}{2} = 0.56 m

Determination of Lever Arms

The moment about the point P is then calculated as:

M_{Ed} = \frac{|H_{t, x}|}{4} \cdot (a_{3, y} + a_{4, y}) - \frac{|H_{t, x}|}{2} \cdot a_{2, y} = \frac{|289.01 kN|}{4} \cdot (0.31 m + 0.56 m) - \frac{|289.01 kN|}{2} \cdot 0.08 = 52.02 kNm

Bending Design Moment of Bucket Wall in y-Direction

This bending design moment M_Ed must be balanced by an opposing moment. This is generated by the concrete compression force on the compressed inner side of the bucket wall in the y-direction with the lever arm z to the rotation point P. To determine the required concrete compression, proceed as follows:

It is assumed that the concrete stress is uniformly distributed over the compression area.
Starting from a concrete strain of 0.0 ‰, it is incrementally increased until the resulting internal moment equals the bending design moment M_Ed.

At the same time, it is assumed that the steel on the outer side of the bucket wall has already reached its maximum strain. Once the calculated internal moment exceeds the bending design moment M_Ed, the iteration is stopped.

At the end of the iteration, the following values were obtained:

Designation	Value
Required reinforcement area A_s,w,req	5.60 cm²
Bending design moment M_Ed	52.02 kNm
Lever arm of internal forces z	0.21 m
Used neutral axis depth x	0.04 m
Reinforcement strain on tension side ε_s	18.90 ‰
Reinforcement stress on tension side σ_s	449.899 N/mm²
Reinforcement strain on compression side ε_s,c	1.2 ‰
Reinforcement stress on compression side σ_s,c	247.515 N/mm²
Concrete strain on compression side ε_c	-3.5 ‰
Concrete stress on compression side σ_c	-19.833 N/mm²
Concrete compression force F_c	252.07 kN
Tensile force F_s	252.07 kN

The required reinforcement area in the bucket due to the bending is 5.60 cm². This bending tensile force does not distribute evenly over both horizontal stirrups, but follows the compression strut mechanism. More information can be found in the Concrete Foundations manual.

Angle of Dispersal

To determine the tension component absorbed by the outer bucket stirrup, follow these steps:

Determine the vertical and horizontal leg of the concrete compression strut within the bucket wall:

\{\begin{cases} a_{5, x} = d_{x (Wand)} - k_{x (Wand)} - \frac{X_{x (Wand)}}{4} = 0.223 m - 0.832 \cdot \frac{0.04 m}{4} = 0.21 m \\ a_{6, y} = \frac{d_{b, y}}{2} - \frac{3}{8} \cdot c_{y} - c_{(k)} - \frac{d_{s, h}}{2} = \frac{1.24 m}{2} - \frac{3}{8} \cdot 0.30 m - 0.05 m - \frac{0.014 m}{2} = 0.45 m \end{cases}

Vertical and Horizontal Lever Arms of Concrete Compression Strut Within Bucket Wall

Distribution angle of the load within the bucket wall:

θ_{1, x} = \arctan (\frac{a_{5, x}}{a_{6, y}}) = \arctan (\frac{0.21 m}{0.45 m}) = 25.39 °

Angle of Dispersal Within Bucket Wall

Proportional compression force in outer stirrups due to bending of the bucket wall:

P_{1, x (wall)} = \frac{|H_{t, x}|}{4 \cdot \sin (θ_{1, x})} = \frac{|289.01 kN|}{4 \cdot \sin (25.39 °)} = 168.48 kN

Proportional Compressive Force in Outer Stirrup Due to Bending of Bucket Wall

Proportional tensile force in outer stirrups due to bending of the bucket wall:

T_{h, out, x (Wand)} = P_{1, x (Wand)} \cdot \cos (θ_{1, x}) = 168.48 kN \cdot \cos (25.39 °) = 152.20 kN

Proportional Tensile Force in Outer Stirrups Due to Bending of Bucket Wall

The required reinforcement area of the outer horizontal stirrups in the bucket due to bending of Ht,x is:

Required Reinforcement Area of Horizontal Outer Stirrups in Bucket Due to Bending of Ht,x

Similarly to the bucket wall in the y-direction, the bending failure of the bucket wall in the x-direction due to H_T,y is calculated, and the required reinforcement area of the outer horizontal stirrups in the bucket due to the bending of H_t,y A_sw,h,out,erf(M_Ed|H_t,y) is determined. It results to 0.76 cm². As explained above, it is necessary to add both bending and tension components to determine the required reinforcement area of the outer horizontal stirrups in the bucket:

The required reinforcement area of the outer horizontal stirrups in the bucket due to the bending of H_t,x A_sw,h,out,req(M_Ed|H_t,x) is added to the required reinforcement area of the horizontal stirrups in the bucket due to the tensile force in the y-direction A_sw,h,req(H_t,y).
The required reinforcement area of the outer horizontal stirrups in the bucket due to the bending of H_t,y A_sw,h,out,req(M_Ed|H_t,y) is added to the required reinforcement area of the horizontal stirrups in the bucket due to the tensile force in the x-direction A_sw,h,req(H_t,x).

A_{sw, \erf, B, h} = \{\begin{cases} (A_{sw, h, \erf} (H_{t, x}) + A_{sw, h, out, \erf} (M_{Ed} | H_{t, y}) = 1.66 cm ² + 0.76 cm ² = 2.42 cm ² \\ (A_{sw, h, \erf} (H_{t, y}) + A_{sw, h, out, \erf} (M_{Ed} | H_{t, x}) = 0.66 cm ² + 3.50 cm ² = 4.17 cm ² \end{cases}

Required Reinforcement Area of Horizontal Outer Stirrups in Bucket

Required Horizontal Reinforcement in y-Direction

First, consider the horizontal stirrup located on the outer side of the bucket wall in the y-direction. Load Combination 2 (LC1+LC3) results in the largest required reinforcement area of the horizontal stirrups in the y-direction and is thus governing.

3D structural model display: reinforcement analysis in the y-direction with detailed element views.

Determination of Reinforcement in y-Direction

As seen in the image above, it is assumed that only horizontal forces in the x-direction lead to tensile forces in this stirrup. For more information, see the Concrete Foundations manual.

The required reinforcement area of the horizontal stirrups in the y-direction in the bucket due to the bending of H_t,x is determined from the total required bending reinforcement of the wall in the y-direction, minus the component already absorbed by the outer stirrups. For Load Combination 2 (LC2), the total required reinforcement area due to bending in the y-direction is 5.83 cm². Of this, 3.63 cm² are already absorbed by the outer horizontal stirrups. Thus, the required reinforcement area for the horizontal stirrups in the y-direction in the bucket due to the bending of H_t,x is:

Required Reinforcement Area of Horizontal Stirrups in y-Direction in Bucket Due to Bending of H_t,x

The required reinforcement area of the horizontal stirrups in the bucket due to the tensile force in x-direction must also be considered. It is:

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tension in x-Direction

The required reinforcement area of the horizontal stirrups in the bucket in the y-direction is the maximum of A_sw,h,req(H_t,x) and A_sw,h,in,req (M_Ed|H_t,x):

A_{sw, \erf, B, h, y} = \max \{\begin{array}{l} A_{sw, h, \erf} (H_{t, x}) = 1.72 cm ² \\ A_{sw, h, in, \erf} (M_{Ed} | H_{t, x}) = 2.20 cm ² \end{array} = 2.20 cm ²

Required Reinforcement Area of Horizontal Stirrups in Bucket in y-Direction

Required Horizontal Reinforcement in x-Direction

Similarly to the y-direction reinforcement, only horizontal forces perpendicular to the stirrup leg direction lead to a tensile force in the stirrup. LC3 (LC1+LC4) is governing here.

The reinforcement in the x-direction of a concrete structure is displayed.

Determining Reinforcement in x-Direction

The required reinforcement area of the horizontal stirrups in the bucket in the x-direction is the maximum of A_sw,h,req(H_t,y) and A_sw,h,in,req(M_Ed|H_t,y):

A_{sw, \erf, B, h, x} = \max \{\begin{array}{l} A_{sw, h, \erf} (H_{t, y}) = 0.79 cm ² \\ A_{sw, h, in, \erf} (M_{Ed} | H_{t, y}) = 0.70 cm ² \end{array} = 0.70 cm ²

Required Reinforcement Area of Horizontal Stirrups in Bucket in x-Direction

Required Vertical Reinforcement in x-Direction

To determine the vertical edge reinforcement of the bucket wall in the x-direction, the load case leading to the maximum horizontal force in the x-direction (LC2) is considered. The horizontal force H_t,x = 299.54 kN is evenly distributed over both bucekt wall panels.

The inclination of the concrete compression strut, which forms diagonally across the bucket wall panel in the x-direction, is determined as follows:

Force model for determining the vertical edge pull force

Force Model for Determining Vertical Edge Tension Force

\tan (α_{x}) = \frac{(\frac{5}{6}) \cdot h}{z_{x}} = \frac{(\frac{5}{6}) \cdot h}{0.9 \cdot d_{b, x} - 0.5 \cdot t_{tx}} = \frac{(\frac{5}{6}) \cdot 1.31 m}{0.9 \cdot 1.14 m - 0.5 \cdot 0.27 m} = 1.23

Tangent of Angle of Dispersal Within Bucket Wall

With this, the edge tensile force can be determined:

T_{v, x} = 0.5 \cdot |H_{t, x}| \cdot \tan (α_{x}) = 0.5 \cdot |299.54 k N| \cdot 1.23 = 183.50 k N

Proportional Tensile Force

Only half of the edge tensile force is considered, as the stirrup is double-legged. The resulting required reinforcement is:

A_{sw, \erf, B, v, x} = 0.5 \cdot \frac{T_{v, x}}{f_{yd}} = 0.5 \cdot \frac{183.50 kN}{43.347 kN / cm ²} = 2.11 cm ²

Required Reinforcement Area of Vertical Stirrups in Bucket in x-Direction

The required reinforcement area of vertical stirrups in the bucket in the y-direction is calculated similarly. A required reinforcement area A_sw,req,B,v,y of 0.93 cm² is obtained.

The required bucket reinforcement is listed in the "Concrete Foundations" result table under the "Reinforcement at Foundation" section. Additionally, the reinforcement can be graphically displayed using the Results navigator.

Input of Bucket Reinforcement

Two distribution areas must be used for the outer stirrups. The first distribution area extends over one third of the bucket height. The second distribution area corresponds to the remaining portion of the bucket height. Four stirrups with a diameter of 14 mm are used for each distribution area. The arrangement is identical for the two remaining stirrup groups in the x- and y-directions.

Two stirrups are selected for each edge of the bucket walls in the x- and y-directions. In addition, the bucket walls are structurally reinforced by vertical stirrups spaced 20 cm apart.

Bucket Reinforcement Input

The following two images show the layout and description of the bucket reinforcement:

Horizontal Stirrups | Layout and Description

Vertical reinforcement in the y-direction | Layout and description

Vertical Reinforcement in y-Direction | Layout and Description

Author

Mr. Boukraa supports the development team in the area of reinforced concrete structures where he develops and documents various test scenarios.

;

Required Reinforcement in Bucket with Rough Inner Walls: Design Approach and Steps

Dimensions of Foundation Slab and Bucket

Load Cases

Required Bucket Reinforcement

Required Outer Horizontal Reinforcement

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tension in x-Direction

Required Reinforcement Area of Horizontal Stirrups in Bucket Due to Tension in y-Direction

Required Reinforcement Area of Outer Horizontal Stirrups in Bucket Due to Bending of Ht,x

Required Horizontal Reinforcement in y-Direction

Required Horizontal Reinforcement in x-Direction

Required Vertical Reinforcement in x-Direction

Input of Bucket Reinforcement

Required Reinforcement Area of Outer Horizontal Stirrups in Bucket Due to Bending of H_t,x