Chargement selon EN 1991-1-4 et sécurité au renversement des cylindres circulaires

Facteur de sécurité contre le renversement L'élément de structure risque de se renverser.
Facteur de sécurité contre le renversement = 1 : Le moment de stabilité et le moment de renversement sont égaux. Le modèle est instable et il ne peut pas être exclu qu'il se renverse.
Facteur de sécurité contre le renversement 1 : Le modèle ne risque pas de se renverser.

Exemple

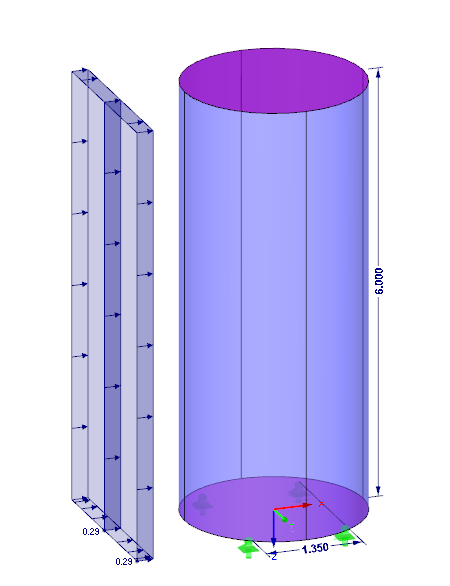
Prenons l'exemple d'un cylindre circulaire d'un diamètre de 2,5 m et d'une hauteur de 6 m. Il est situé dans la zone de charge de vent 2 de catégorie de terrain 3.

Charge de vent

Valeur fondamentale de la vitesse de base :
v_b0 = 25,0 m/s

Facteur directionnel :
c_dir = 1

Coefficient de saison :
c_saison = 1

Densité de l'air à la pression atmosphérique de 1 013 hPa et T = 10° C :
= 1,25 kg/m³

Viscosité cinématique de l'air :
= 15 10 ^-6 m ²/s  

Vitesse de base :
v_b = c_dir ∙ c_saison ∙ v_b0 = 25,0 m/s

Pression dynamique de base :
q_b = 1/2 ρ ∙ v_b ² = 0,391 kN/m²

Pression dynamique maximale :
q_p = 1,5 q_b = 0,586 kN/m²

Vitesse maximale :

Rugosité de surface équivalente :
k = 0,2 mm (acier galvanisé)

Rapport entre la rugosité de surface équivalente et la largeur :
k/b = 8 10 ^-5

Nombre de Reynolds :

Coefficient de force des cylindres sans écoulement libre :

Élancement efficace :
= l/b = 2,4

Facteur d'effet final :
_λ = 0,65

Coefficient de structure :
c_s c_d = 1

Zone de référence :
A_réf = l b = 15 m²

Coefficient de force :
c_f = c_f0λ = 0,498

Force du vent :
F_w = c_s c_d c_f q_p ∙ A_ref = 4,377 kN

Charge surfacique due au vent :
F_w = F_w/A_réf = 0,29 kN/m²

Facteur de stabilité dû au renversement

Hauteur du cylindre circulaire :
h = 6 m

Distance entre les appuis :
a = 1,35 m

Poids propre :
F_G = 18,495 kN

Moment de renversement :
M_K = F_w h/2 = 13,13 kNm

Moment de stabilité :
M_S = F_G a/2 = 12,48 kNm

Facteur de sécurité contre le renversement :
= M_S/M_K = 0,95

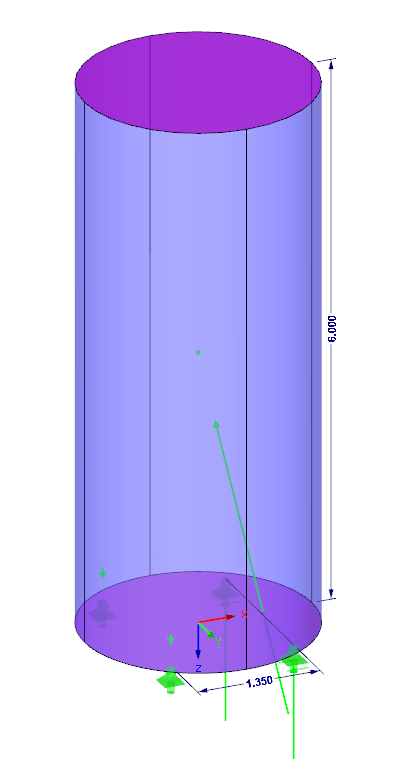
Si vous utilisez RFEM pour le calcul, vous pouvez reconnaître à partir de la position des résultantes qu'elles se trouvent dans son extension derrière le bord de renversement du cylindre circulaire. Le modèle serait donc instable si les appuis n'étaient pas protégés contre l'arrachement.

Lage der Resultierenden