Symulacja metodą obliczeniowej dynamiki płynów (CFD) jest cennym narzędziem w różnych dziedzinach inżynierii, projektowania i badań. W poniższym tekście podkreślamy niektóre z najważniejszych zalet symulacji CFD .
Efektywna kosztowo
Korzystanie z symulacji CFD w dużych lub złożonych układach konstrukcyjnych jest znacznie bardziej opłacalne niż przeprowadzanie eksperymentów fizycznych. Na przykład cyfrowa symulacja przepływu wiatru eliminuje koszty produkcji prototypów, zabezpieczenia obiektów testowych i korzystania ze specjalnego sprzętu.
Oszczędność czasu w symulacjach CFD
Dzięki symulacji CFD można również zaoszczędzić czas w procesie analizy. Szybka konfiguracja i wykonanie odbywa się za pomocą kilku kliknięć, dzięki czemu oszczędza się znacznie więcej czasu niż konfigurowanie testu fizycznego. W ten sposób inżynierowie mogą korzystać z większej liczby iteracyjnych procesów analitycznych . Przetestuj swoje szkice w środowisku wirtualnym i udoskonalaj cyfrowo wszystkie aspekty, zanim ostatecznie zdecydujesz się na odpowiedni fizyczny prototyp.
Szczegółowa wizualizacja
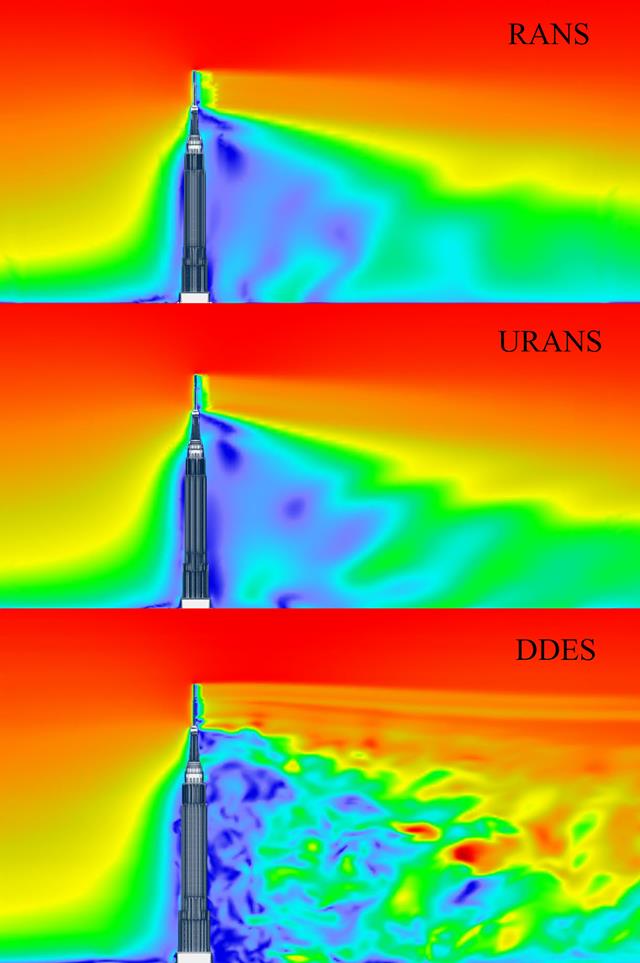
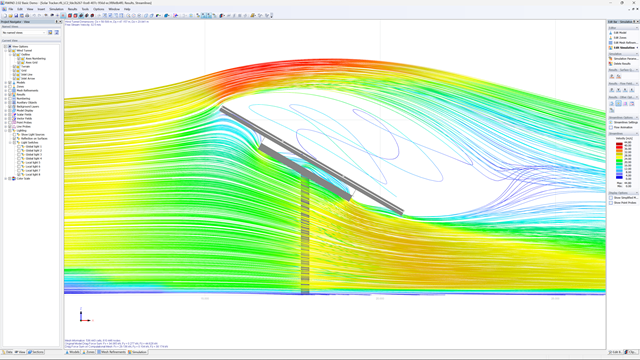
CFD przedstawia na przykład schematy przepływu, rozkłady ciśnienia i inne istotne zjawiska fizyczne , których zweryfikowanie eksperymentalne byłoby trudne lub niemożliwe. Te dodatkowe informacje zapewniają jeszcze lepszy wgląd w dane techniczne projektu.
Skalowalność symulacji CFD
Kolejną zaletą symulacji CFD jest dowolna skalowalność bez większego wysiłku. Chcesz przeanalizować różne rozmiary lub konfiguracje analizy? W cyfrowym tunelu przepływowym jest to łatwo możliwe bez żadnych fizycznych zmian lub bez tworzenia nowych prototypów. Symulacja CFD zapewnia szerszy zakres scenariuszy i parametrów analizy.
Zrównoważony rozwój dzięki symulacjom CFD
Redukując potrzebę budowy fizycznych prototypów i przeprowadzania mniejszej liczby eksperymentów dzięki symulacji CFD, zyskujesz kolejną z zalet symulacji CFD. Niższe zużycie energii i produkcja odpadów są idealnym rozwiązaniem dla osiągnięcia celów zrównoważonego rozwoju, takich jak zmniejszenie kosztów materiałów i aspektów środowiskowych.
Złożoność i dokładność
Cyfrowy tunel aerodynamiczny umożliwia dokładne modelowanie złożonych geometrii i interakcji płynów. Byłoby to trudne do odtworzenia w układzie eksperymentalnym. Dokładność CFD umożliwia analizę subtelnych efektów i interakcji w kontrolowanym środowisku. Jednocześnie program zapewnia złożone analizy, które pomagają w zrozumieniu i optymalizacji układów konstrukcyjnych.
Symulacje CFD są szczególnie przydatne, gdy dobrze rozumiesz leżące u ich podstaw modele i założenia. Aby uzyskać ogólny wynik, najlepszym sposobem jest połączenie symulacji CFD i testów eksperymentalnych. Daje to możliwość pełnego określenia zachowania konstrukcji w sytuacjach przepływu.
Szukasz sposobu na przeprowadzenie symulacji CFD dla swoich projektów ? Wydajny RWIND to samodzielny program, który umożliwia przeprowadzanie symulacji przepływu w różnych sytuacjach. Tutaj można znaleźć więcej informacji na temat najnowszej generacji oprogramowania:
RWIND 2
.
Pokaż więcej