V našem dřívějším příspěvku jsme představili obecnou metodu výpočtu a modelování průvlaků, žeber a deskových nosníků ve stavu porušeném trhlinami.
Na následujících řádcích popíšeme posouzení na spojitém železobetonovém nosníku. Výpočet lze provést v přídavných modulech CONCRETE a RF‑CONCRETE Members v kombinaci s rozšířeními EC2 a RF‑CONCRETE NL.
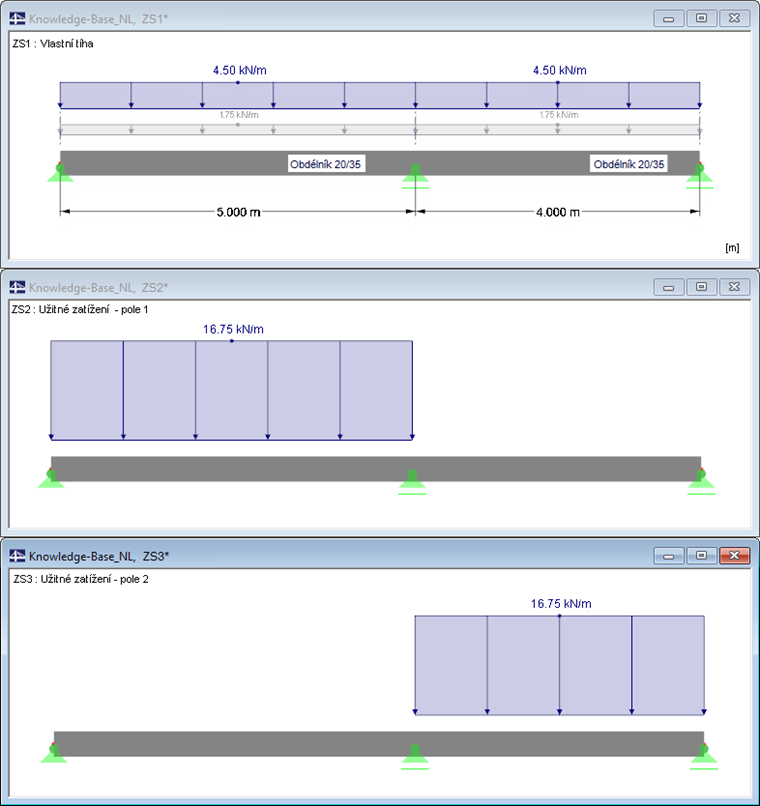
Konstrukce a zatížení
Spojitý nosník z betonu C30/37 má obdélníkový průřez 20/35 cm.
Stálá a užitná zatížení jsou uspořádána do tří zatěžovacích stavů. Návrhové kombinace podle EN 1990 necháme automaticky vygenerovat pro mezní stav únosnosti a použitelnosti (častá návrhová situace) v programu RFEM/RSTAB.
Lineární výpočet výztuže v MSÚ
Nejdříve vypočítáme výztuž v mezním stavu únosnosti. Při výpočtu se uvažuje redistribuce a redukce momentů v případě vnitřních sil kombinace výsledků KV1. Dále se stanoví následující parametry výztuže:
- Průměr výztuže 16 mm
- Odstupňování výztuže ve třech oblastech
- Krycí betonová vrstva 30 mm
- Minimální horní a dolní výztuž 2 Ø 12
- Konstrukční výztuž Ø 12 s maximální vzdáleností výztuže 15 cm
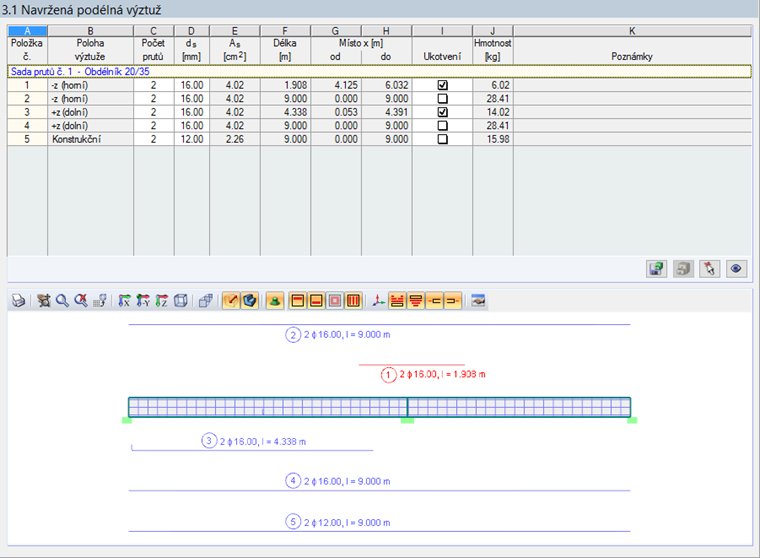
Na základě zadaných údajů spustí program lineárně pružný výpočet a stanoví návrh výztuže. V dialogu 3.1 můžeme tuto výztuž, která poslouží jako základ pro nelineární výpočet, překontrolovat.
Nelineární výpočet šířky trhlin a deformací v MSP
Pro nelineární výpočet mezního stavu použitelnosti vybereme kombinace zatížení KZ6 až KZ8 (u kombinací výsledků nelze určit jednoznačné vztahy mezi napětím a protažením). Při nelineární analýze se budou uvažovat účinky tahového zpevnění. Použijeme proto upravenou charakteristickou křivku oceli podle [2].
![Dialog v modulu CONCRETE „Základní údaje“ pro mezní stav použitelnosti s detailním nastavením nelineárního výpočtu podle [2]](/cs/webimage/009376/2418463/03-cs-png.png?mw=760&hash=b667ba64adf49a87aab98e1c3b6927bb5aadd8b4)
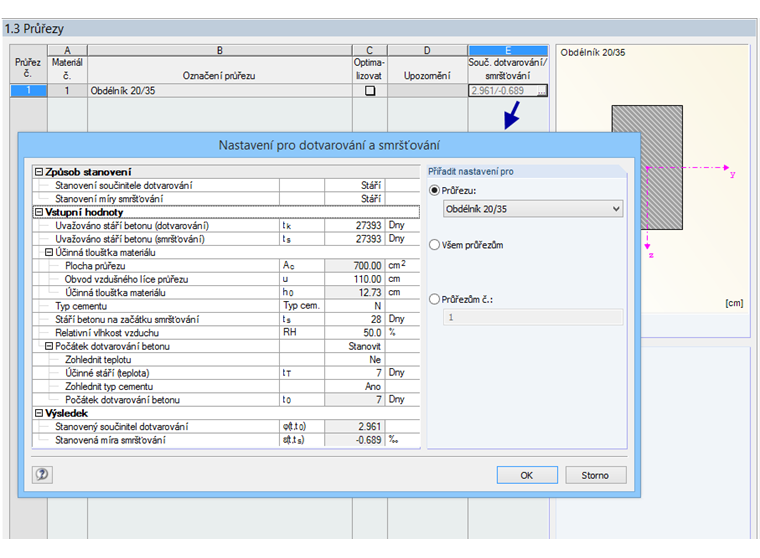
Dále se zohlední také účinky dotvarování a smršťování. Příslušné nastavení lze provést v dialogu 1.3.
Výsledky
Provede se fyzikální a geometrický nelineární výpočet. Iterace poměrného přetvoření přitom probíhá v rovině průřezu. Vychází se z průběhu vnitřních sil v daném iteračním cyklu a počítají se stále nové, aktuální stavy napětí a přetvoření. Konvergence nastává, jakmile je dosažen rovnovážný stav.
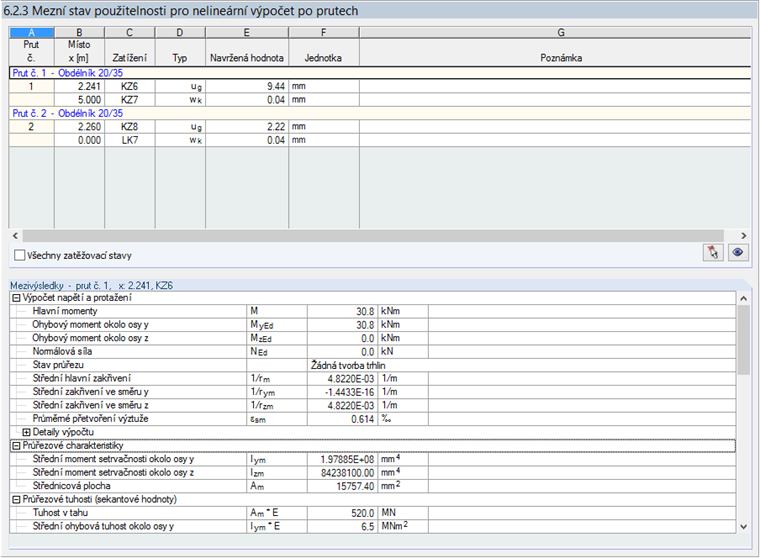
Největší deformace lze podle očekávání zaznamenat v poli 1 v případě zatížení z kombinace KZ6 (ZS1 + 0,5 ∙ ZS2). Šířka trhlin je nepatrná.
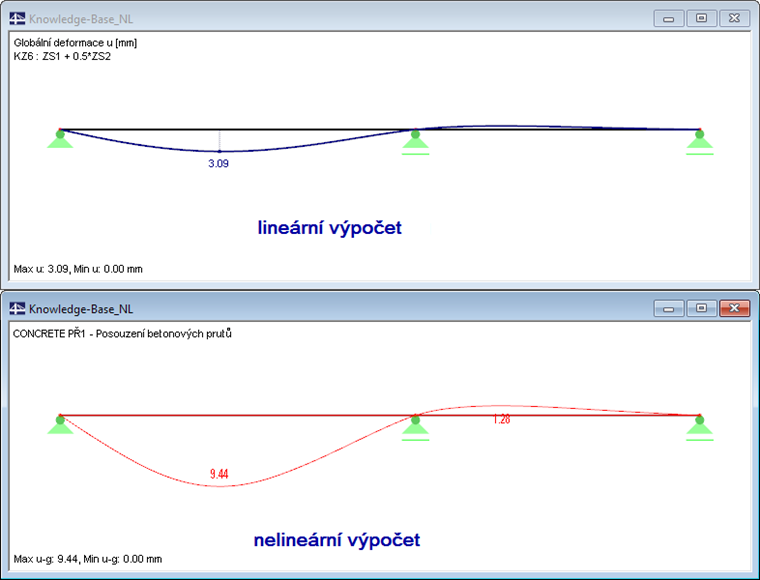
Deformace, která vyplývá z nelineárního výpočtu, při němž se zohledňuje vliv dotvarování, je výrazně větší než deformace stanovená při čistě lineárně pružném výpočtu bez uvažování vlivu dotvarování. Rozdíl je patrný, pokud deformace porovnáme na následujícím obrázku.
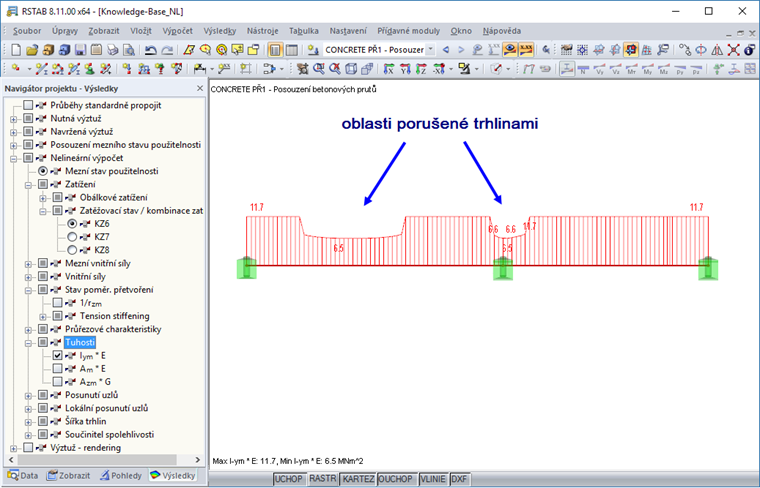
Jak je zřejmé z diagramu tuhosti, velká oblast pole 1 je ve stavu použitelnosti porušena trhlinou.
Závěr a výhled
V porovnání s lineárně pružným výpočtem železobetonových prvků můžeme při nelineární analýze tuhostí a protažení dospět k hodnotám, které jsou při zohlednění tvorby trhlin výrazně vyšší. V programech společnosti Dlubal Software lze tyto účinky zohlednit v modulech pro železobetonové konstrukce, pokud vybereme nelineární metodu výpočtu. Přitom lze uvažovat také vliv dotvarování a smršťování.