General
Each nodal support has its own local axis system. The axes are defined as X', Y', and Z'. This axis system is based on the global axis system of the RFEM or RSTAB file by default. However, it is possible to define a custom axis system or simply a rotation. In the example shown here, the support axis systems are displayed for all nodal supports.
The options of the individual nonlinearities will be shown for the rotation around Y'. Similar definitions apply for the other two support axis directions. The positive rotation direction of moment follows the right-hand rule.
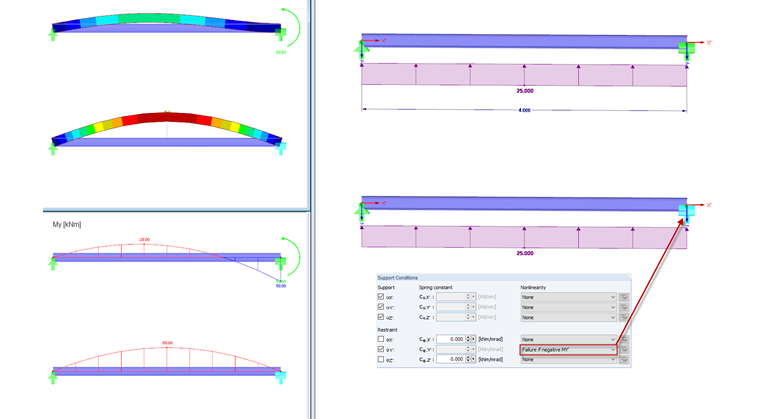
Note: The nonlinearity always refers to the acting support force.
Failure if MY' Negative
The Y'-axis is oriented towards us. Thus, a left-turning support moment is positive. The entered loading generates a support moment turning to the right in the support and thus, the support moment is negative.
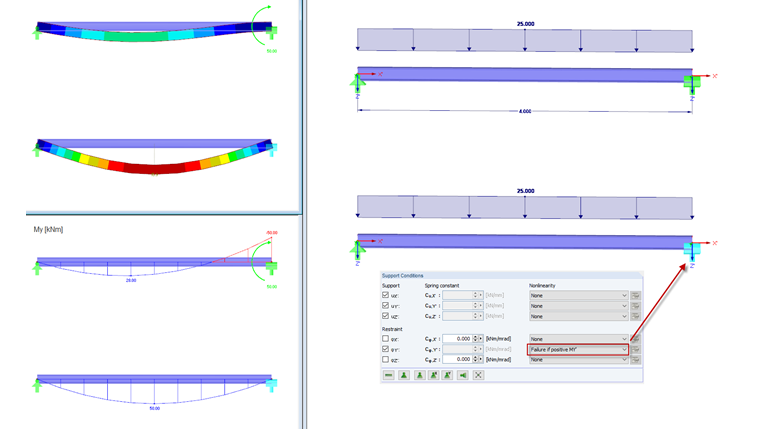
Failure if MY' Positive
The Y'-axis is oriented towards us. Thus, a left-turning support moment is positive. The entered loading generates a support moment turning to the left in the support and thus, the support moment is positive.
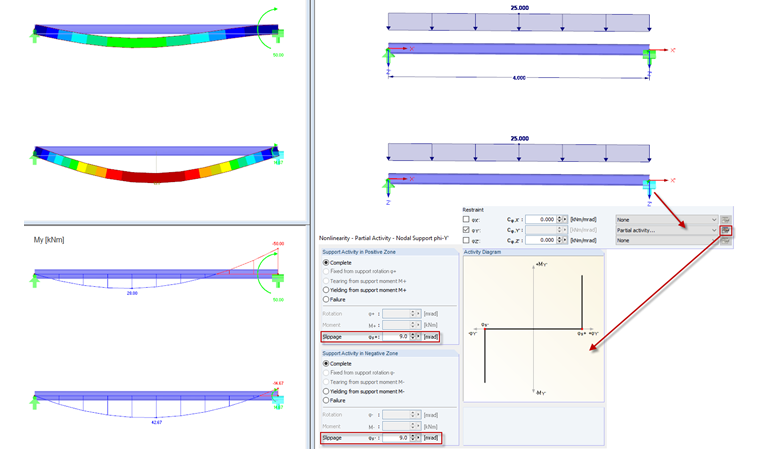
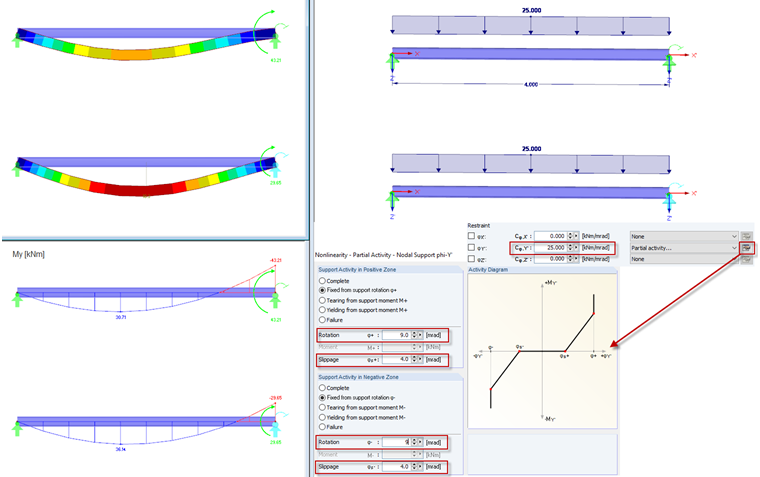
Partial Activity: Slippage
The partial activity is defined in an additional menu. Here, it is possible to define the support for the positive zone independently (positive support moment MY' and positive rotation φY') as well as for the negative zone (negative support moment MY' and negative rotation φY'). The settings are then displayed graphically in a diagram.
If the support has been defined as "fixed" in Y', the support node with the defined "complete" and "slippage" support activity is rotated until the defined slippage occurs. Then, the acting support moment will be transferred completely. If a spring has been defined, it is effective after reaching the defined slippage.
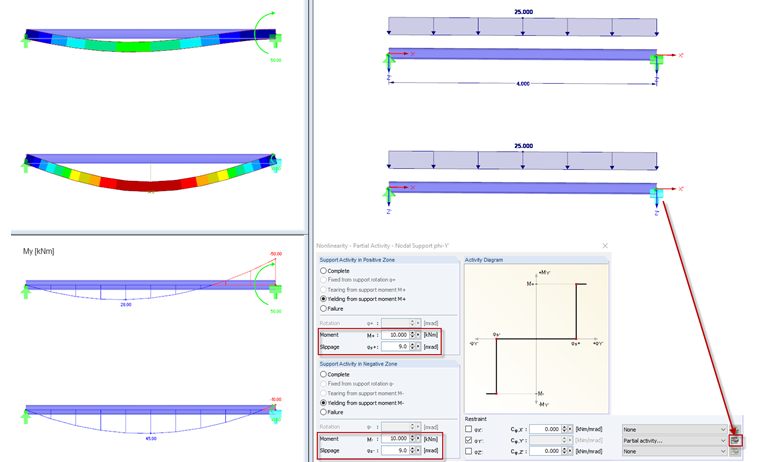
Partial Activity: Yielding and Slippage
By selecting this option, you can define a limit support moment and a value for the slippage. Again, this can be done independently for the positive and the negative zones. If a greater rotation than the defined slippage is reached, the support can only transfer the defined limit support moment. If the acting support moment exceeds the limit support moment, the rotation continues to increase without increase of the support moment.
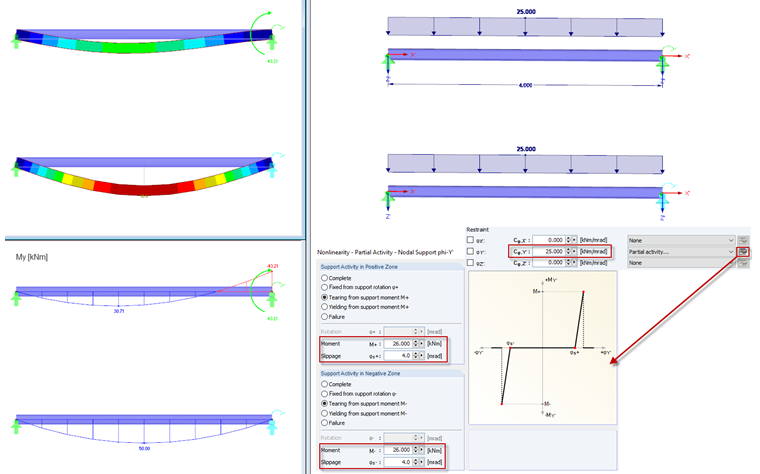
Partial Activity: Spring and Slippage
If a spring constant has been defined for the support, an additional option called "Fixed from support rotation φ+" is available for "Partial activity". As already described, it is possible to define a limit value for the slippage. Furthermore, the activity of the defined spring is now limited by the limiting value "Rotation". A linear rotational spring operates between the limiting value "Slippage" and the limiting value "Rotation". If the deformation becomes greater than the limiting value "Rotation", the support moment is absorbed completely without further increase of the rotation. As with all other options, this can also be defined separately for the positive and the negative zones.
Partial Activity: Tearing from Support Moment
If a spring constant has been defined for the support, it is also possible to specify "Tearing from support moment M+" for the support. This option can again be combined with slippage. The support moment increases accordingly with regard to the rotational spring constant until the defined limit support moment is reached. If the limit support moment is exceeded, the support fails suddenly for this restraint.
Another technical article will describe the other options that have not been explained here.























































.png?mw=600&hash=49b6a289915d28aa461360f7308b092631b1446e)
