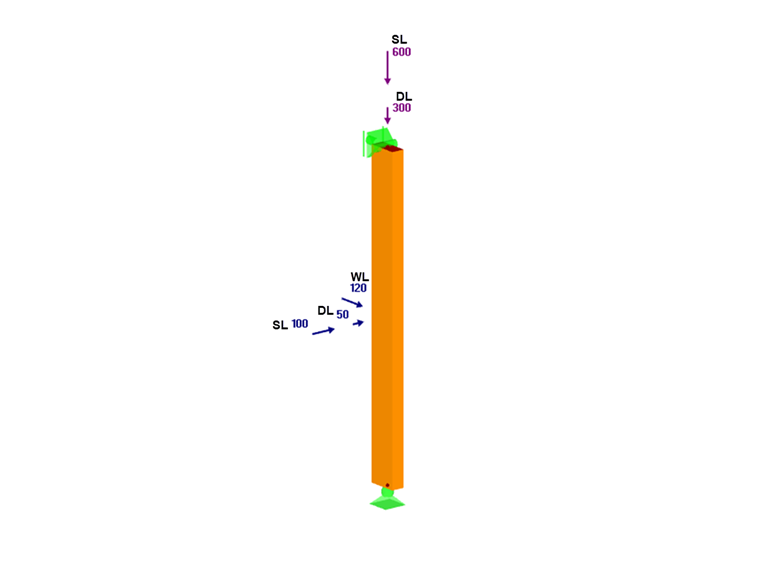
Timber Beam-Column Design as per NDS 2018 Using RF-/TIMBER AWC Module

Technical Article

Back to Knowledge Base

KB 001714 | Timber Beam-Column Design per NDS 2018 Using RF-/TIMBER AWC Module

Back to Knowledge Base

06/14/2021

001714

Cisca Tjoa

Technical Article

Design

RFEM US Timber Package 5.xx

In this article, the adequacy of a 2x4 dimension lumber subject to combined biaxial bending and axial compression is verified using the RF-/TIMBER AWC add-on module. The beam-column properties and loading are based on example E1.8 of AWC Structural Wood Design Examples 2015/2018.

The member is a No. 2 Southern Pine, 2x4 nominal, 3 feet long and used as a truss member. Lateral support is provided only at the member ends, and they are considered pinned. The dead (DL), snow (SL), and wind (WL) loads are applied at the top and midpoint of the beam-column, as shown below.

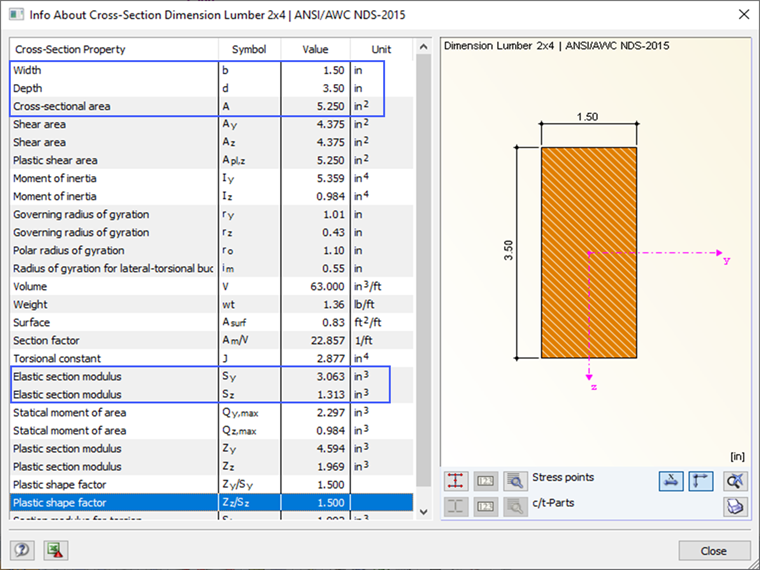
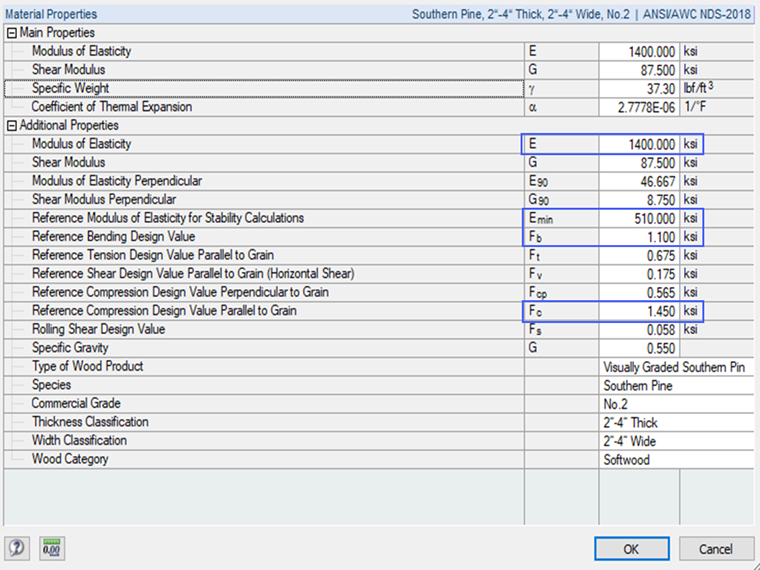
The member properties are shown after selecting the appropriate cross-section and material in the program.

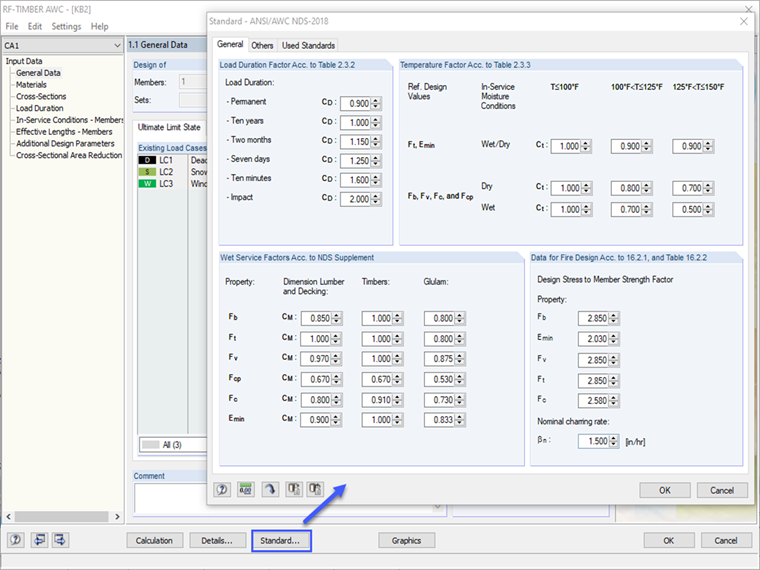
Adjustment Factors Listed in Table 4.3.1 of NDS 2018 for ASD Design

The reference design values (F_b, F_c, and E_min) are multiplied by the applicable adjustment factors to determine the adjusted design values. For sawn lumber, these factors are found in Table 4.3.1 [1]. There are eleven different adjustment factors for the ASD design. Many of these factors are equal to 1.0 in the NDS example [2]. However, brief description and how RF-/TIMBER AWC accounts for each factor is given below.

Factors Calculated by the Program

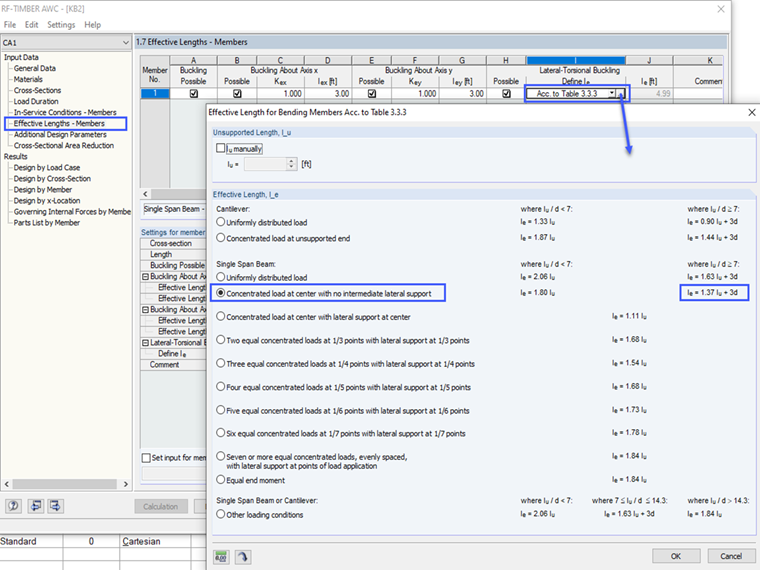
C_L ... Beam Stability Factor. It depends on the geometry and lateral support of the member as described in Section 3.3.3 [1]. This factor is automatically calculated in RF-/TIMBER. (Note: the effective length, le, used to calculate C_L is defined by the user in the 'Effective Length' section of RF-/TIMBER AWC. The option "Acc. to Table 3.3.3" with the appropriate loading case must be selected.) The image below shows the applicable loading case for this example.

C_F ... Size Factor. It depends on the depth and thickness of the member as specified in Section 4.3.6 [1]. This factor is automatically determined in RF-/TIMBER AWC.

C_fu ... Flat Use Factor. It accounts for weak axis bending of the member as specified in Section 4.3.7 [1]. This factor is automatically calculated in RF-/TIMBER AWC.

C_P ... Column Stability Factor. It depends on the geometry, end fixity conditions, and lateral support of the member as described in Section 3.7.1 [1]. When a compression member is fully supported throughout its length, C_P = 1.0. This factor is automatically calculated in RF-/TIMBER AWC for both strong and weak axis directions.

Factors Defined by User Input

C_D ... Load Duration Factor. It accounts for various loading periods based on the load case, such as dead, snow, and wind, based on Section 4.3.2 [1]. Selecting "ASCE 7-16 NDS (Wood)" as the standard in RFEM activates the load duration option in the Load Cases dialog box. The load duration class (Permanent, Ten Years, and so on) default setting is based on the 'Action Category' of the load case. This setting can be adjusted by the user in RFEM or RF-/TIMBER AWC. The value selected by the program is based on Table 2.3.2 [1].

C_M ... Wet Service Factor. It accounts for the moisture service conditions of the member as specified in Section 4.1.4 [1]. The user can select "wet" or "dry" in the 'In-Service Conditions' section of RF-/TIMBER AWC.

C_t ... Temperature Factor. It accounts for exposure to elevated temperatures of up to 100 degrees F, 100 to 125, and 125 to 150 as described in Section 2.3.3 [1]. The user can select between the three temperature ranges in the 'In-Service Conditions' section of RF-/TIMBER AWC. The value selected by the program is based on Table 2.3.3 of [1].

C_i ... Incising Factor. It accounts for the loss of the area from the small incisions made in the member to receive preservative treatment for decay prevention as described in Section 4.3.8 [1]. The user can select "Not Incised" or "Incised" in the 'Additional Design Parameters' section of RF-/TIMBER AWC.

C_r ... Repetitive Member Factor. It is used when multiple members act compositely to properly distribute a load amongst themselves as described in Section 4.3.9 [1]. C_r = 1.15 for members that meet the criteria of being closely spaced and connected by a sheathing or equivalent. The user can select "Not Repetitive" or "Repetitive" in the 'Additional Design Parameters' section of RF-/TIMBER AWC.

Note: If necessary, code-based values of the user input adjustment factors can be changed in the 'Standard' option.

Factors Excluded in the Program

C_T ... Buckling Stiffness Factor. It accounts for the contribution of plywood sheathing to the buckling resistance of compression truss chords as specified in Section 4.4.2 [1]. This factor is used to increase E_min of the member. C_T can be manually calculated as per equation 4.4-1 [1] or conservatively taken as 1.0.

C_b ... Bearing Area Factor. It is used to increase the compression design values (F_cp) for concentrated loads applied perpendicular to the grain as specified in Section 3.10.4 [1]. C_b can be manually calculated per equation 3.10-2 [1] or conservatively taken as 1.0.

Actual Stress in the Beam-Column

In this example, the load combination has been simplified to CO1: DL + SL + WL.

Compression stress from dead and snow loads, f_c = 171 psi

Strong-axis bending stress from wind load, f_bx = f_b1 = 353 psi

Weak-axis bending stress from dead and snow loads, f_by = f_b2 = 1,029 psi

Determine the Adjusted Design Values as per NDS 2018 Table 4.3.1 ASD Method

Critical Buckling Design Value for Compression Member in Strong Axis, F_cEx

Critical Buckling Design Value for Compression Member in Strong Axis, FcEx

$F_{cEx} = F_{cE 1} = \frac{0.822 \cdot E_{\min}'}{{[\frac{l_{e 1}}{d_{1}}]}^{2}} F_{cEx} = F_{cE 1} = \frac{0.822 \cdot 510, 000 psi}{{[\frac{36.0 in}{3.5 in}]}^{2}} F_{cEx} = F_{cE 1} = 3, 963 psi$

F_cEx	Critical buckling design value for compression member in strong axis, psi
E_min'	= E_min ⋅ C_M ⋅ C_T ⋅ C_i = 510,000 psi
l_e1	Effective length = 36.0 in
d₁	Depth of member = 3.5 in

Critical Buckling Design Value for Compression Member in Weak Axis, F_cEy

Critical Buckling Design Value for Compression Member in Weak Axis, FcEy

$F_{cEy} = F_{cE 2} = \frac{0.822 \cdot E_{\min}'}{{[\frac{l_{e 2}}{d_{2}}]}^{2}} F_{cEy} = F_{cE 2} = \frac{0.822 \cdot 510, 000 psi}{{[\frac{36.0 in}{1.5 in}]}^{2}} F_{cEy} = F_{cE 2} = 728 psi$

F_cEy	Critical buckling design value for compression member in weak axis, psi
E_min'	= E_min ⋅ C_M ⋅ C_T ⋅ C_i = 510,000 psi
l_e2	Effective length = 36.0 in
d₂	Thickness of member = 1.5 in

Adjusted Compressive Design Value Parallel to Grain, F_c'

Adjusted Compressive Design Value Parallel to Grain, Fc'

$F_{c}' = F_{cy}' = F_{c} \cdot C_{D} \cdot C_{M} \cdot C_{t} \cdot C_{F} \cdot C_{i} \cdot C_{P} F_{c}' = F_{cy}' = 1, 450 psi \cdot 1.6 \cdot 1.0 \cdot 1.0 \cdot 1.0 \cdot 1.0 \cdot 0.29 F_{c}' = F_{cy}' = 673 psi$

F_c'	Adjusted compressive design value parallel to grain, psi
F_c	Reference compressive design values parallel to grain, psi
C_D	Load duration factor
C_M	Wet service factor
C_t	Temperature factor
C_F	Size factor
C_i	Incising factor
C_P	Column stability factor

Critical Buckling Design Value for Bending Member, F_bE

Critical Buckling Design Value for Bending Member, FbE

$F_{bE} = \frac{1.20 \cdot E_{\min}'}{{R_{B}}^{2}} F_{bE} = \frac{1.20 \cdot 510, 000 psi}{{9.65}^{2}} F_{bE} = 6, 577 psi$

F_bE	Critical buckling design value for bending member, psi
E_min'	= E_min ⋅ C_M ⋅ C_T ⋅ C_i = 510,000 psi
R_B	Slenderness ratio = 9.65 < 50 (NDS equation 3.3-5)

Adjusted Strong Axis Bending Design Value, F_bx'

Adjusted Strong Axis Bending Design Value, Fbx'

$F_{bx}' = F_{b 1} = F_{b} \cdot C_{D} \cdot C_{M} \cdot C_{L} \cdot C_{t} \cdot C_{F} \cdot C_{i} \cdot C_{r} F_{bx}' = F_{b 1} = 1, 100 psi \cdot 1.6 \cdot 1.0 \cdot 0.982 \cdot 1.0 \cdot 1.0 \cdot 1.0 \cdot 1.0 F_{bx}' = F_{b 1} = 1, 729 psi$

F_bx'	Adjusted strong axis bending design value, psi
F_b	Reference bending design value, psi
C_D	Load duration factor
C_M	Wet service factor
C_L	Beam stability factor
C_t	Temperature factor
C_F	Size factor
C_i	Incising factor
C_r	Repetitive member factor

Adjusted Weak Axis Bending Design Value, F_by'

Adjusted Weak Axis Bending Design Value, Fby'

$F_{by}' = F_{b 2} = F_{b} \cdot C_{D} \cdot C_{M} \cdot C_{L} \cdot C_{t} \cdot C_{fu} \cdot C_{F} \cdot C_{i} \cdot C_{r} F_{by}' = F_{b 2} = 1, 100 psi \cdot 1.6 \cdot 1.0 \cdot 1.0 \cdot 1.0 \cdot 1.1 \cdot 1.0 \cdot 1.0 \cdot 1.0 F_{by}' = F_{b 2} = 1, 936 psi$

F_by'	Adjusted weak axis bending design value, psi
F_b	Reference bending design value, psi
C_D	Load duration factor
C_M	Wet service factor
C_L	Beam stability factor
C_t	Temperature factor
C_fu	Flat use factor
C_F	Size factor
C_i	Incising factor
C_r	Repetitive member factor

Combined Biaxial Bending and Axial Compression Design Ratio

Inserting the actual stresses and limiting design values presented above into NDS equation 3.9-3 [1], the final design ratio is shown below.

Combined Bi-axial Bending and Axial Compression Design Ratio

${(\frac{f_{c}}{F_{c}'})}^{2} + \frac{f_{bx}}{F_{bx}' \cdot [1 - (\frac{f_{c}}{F_{cEx}})]} + \frac{f_{by}}{F_{by}' \cdot [1 - (\frac{f_{c}}{F_{cEy}}) - {(\frac{f_{bx}}{F_{bE}})}^{2}]} ⩽ 1.0 {(\frac{171}{673})}^{2} + \frac{353}{1, 729 \cdot [1 - (\frac{171}{3, 965})]} + \frac{1, 029}{1, 936 \cdot [1 - (\frac{171}{728}) - {(\frac{353}{6, 577})}^{2}]} = 0.98$

f_c	Compression stress from dead and snow load
F_c'	Adjusted compressive design value parallel to grain
f_bx	Strong-axis bending stress from wind load
F_bx'	Adjusted strong axis bending design value
F_cEx	Critical buckling design value for compression member in strong axis
f_by	Weak-axis bending stress from dead and snow load
F_by'	Adjusted weak axis bending design value
F_cEy	Critical buckling design value for compression member in weak axis
F_bE	Critical buckling design value for bending member

And NDS equation 3.9-4 [1],

Combined Bi-axial Bending and Axial Compression Design Ratio

$\frac{f_{c}}{F_{cEy}} + {(\frac{f_{bx}}{F_{bE}})}^{2} \leq 1.0 \frac{171}{728} + {(\frac{353}{6, 577})}^{2} = 0.24$

f_c	Compression stress from dead and snow load
F_cEy	Critical buckling design value for compression member in weak axis
f_bx	Strong-axis bending stress from wind load
F_bE	Critical buckling design value for bending member

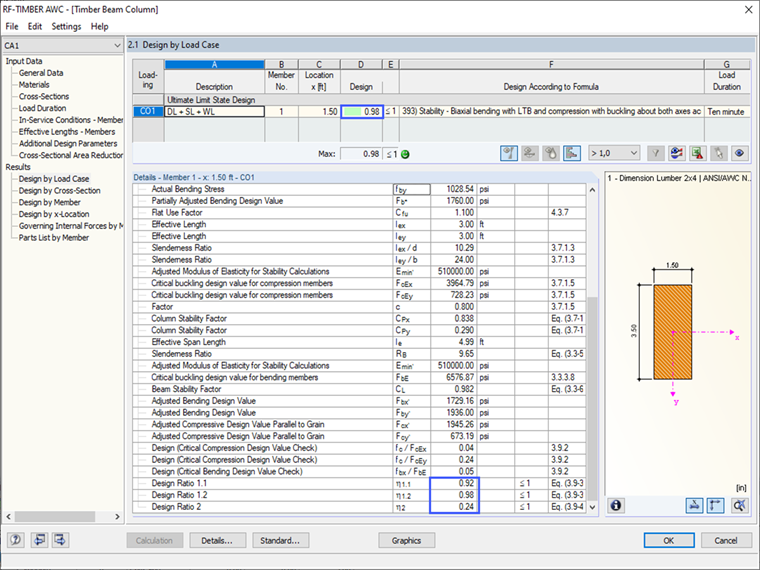
Result in RF-/TIMBER AWC

The user can compare each adjustment factor and adjusted design value from the analytical hand calculation method to the result summary in RF-/TIMBER AWC. As shown, the results are identical. The controlling final design ratio = 0.98 is based on the geometrically linear analysis (1^st degree) calculation method. Keep in mind that the default setting in RFEM for the load combination is set to the second-order analysis. This will result in a slightly larger design ratio = 1.03. The user has the option to choose which method listed in the 'Calculation Parameters' is best for the structure.