Projektowanie drewnianej belki-słupa zgodnie z NDS 2018 przy użyciu modułu RF-/TIMBER AWC

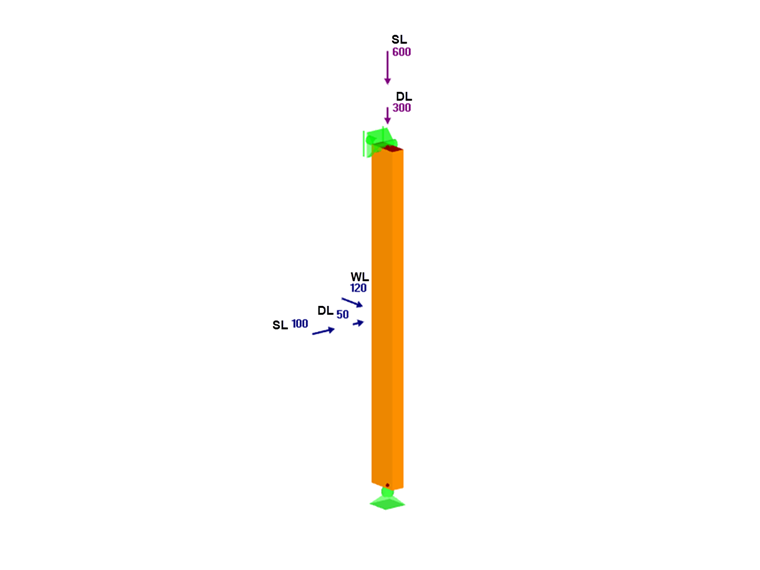
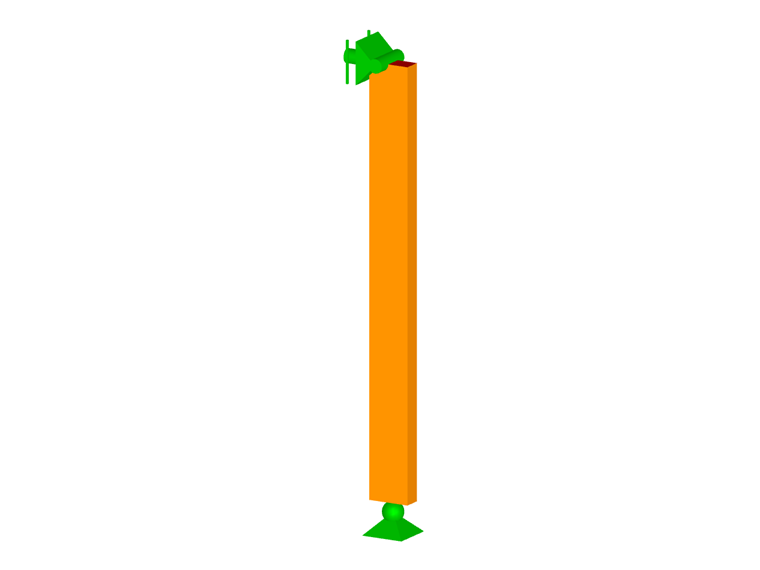
Człon jest wykonany z sosny południowej Nr 2, nominalne 2x4, o długości 3 stóp, używany jako element kratownicy. Podparcie boczne jest zapewnione tylko na końcach członu, które są uznawane za przegubowe. Obciążenia stałe (DL), śniegowe (SL) i wiatrowe (WL) są przykładane na górze i w połowie wysokości belki-kolumny, jak pokazano poniżej.

• 3D Viewer
• 3D Viewer | Babylon
• Wirtualna rzeczywistość

Belka-słup drewniany

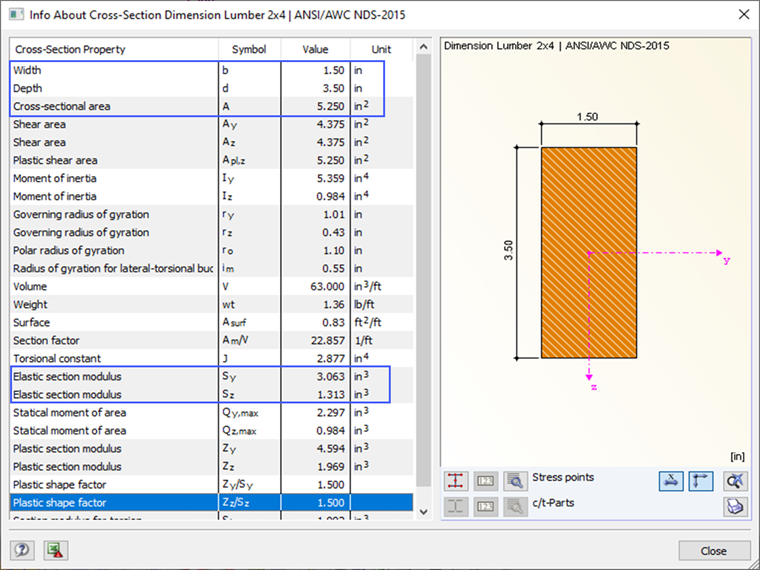
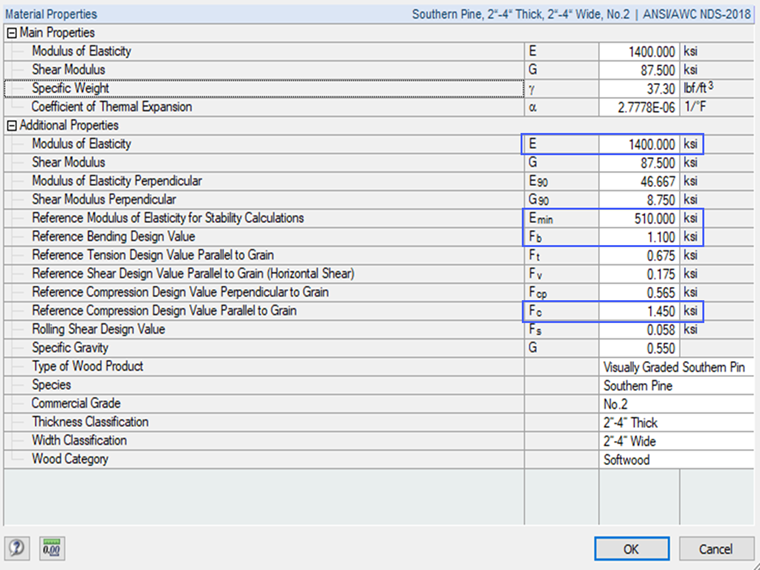
Właściwości elementu są pokazywane po wybraniu odpowiedniego przekroju i materiału w programie.

Właściwości przekroju poprzecznego tarcicy 2x4

Właściwości materiałowe sosny południowej

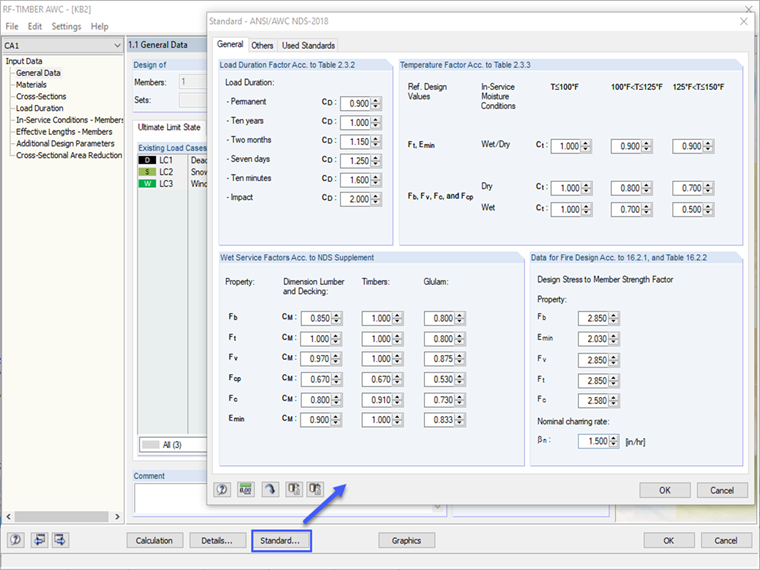
Współczynniki korekcyjne wymienione w Tabeli 4.3.1 NDS 2018 dla projektu ASD

Wartości projektowe odniesienia (F_b, F_c i E_min) są mnożone przez obowiązujące współczynniki korekcyjne, aby określić skorygowane wartości projektowe. Dla drewna ciętego czynniki te znajdują się w Tabeli 4.3.1 [1]. Istnieje jedenaście różnych współczynników korekcyjnych dla projektu ASD. Wiele z tych współczynników jest równe 1.0 w przykładzie NDS [2]. Jednakże poniżej znajduje się krótki opis i sposób, w jaki RF-/TIMBER AWC uwzględnia każdy z czynników.

Czynniki obliczane przez program

C_L – Współczynnik stabilności belki

Zależy od geometria i bocznego podparcia członu, jak opisano w Sekcji 3.3.3 [1]. Ten współczynnik jest automatycznie obliczany w RF-/TIMBER.

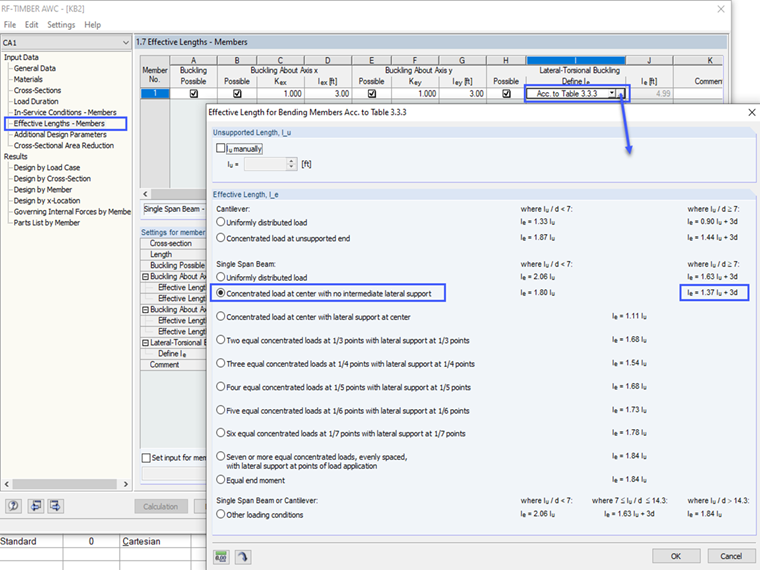
Uwaga: efektywna długość, l_e, użyta do obliczenia C_L jest definiowana przez użytkownika w sekcji "Efektywna długość" RF-/TIMBER AWC. Należy wybrać opcję "Zgodnie z Tabelą 3.3.3" z odpowiednim przypadkiem obciążenia.

Poniższy obrazek pokazuje obowiązujący przypadek obciążenia dla tego przykładu.

Długość efektywna dla współczynnikaC L.

C_F – Współczynnik rozmiaru

Zależy od głębokości i grubości członu, jak określono w Sekcji 4.3.6 [1]. Ten współczynnik jest automatycznie określany w RF-/TIMBER AWC.

C_fu – Współczynnik płaskiego użytkowania

Uwzględnia zginanie osi słabej członu, jak określono w Sekcji 4.3.7 [1]. Ten współczynnik jest automatycznie obliczany w RF-/TIMBER AWC.

C_P – Współczynnik stabilności kolumny

Zależy od geometria, warunków końcowych i bocznego podparcia członu, jak opisano w Sekcji 3.7.1 [1]. Gdy człon w kompresji jest w pełni podparty na całej długości, C_P = 1.0. Ten współczynnik jest automatycznie obliczany w RF-/TIMBER AWC dla obu kierunków osi: mocnej i słabej.

Czynniki definiowane przez dane wejściowe użytkownika

C_D – Współczynnik czasu trwania obciążenia

Uwzględnia różne okresy oddziaływania obciążenia na podstawie przypadku obciążenia, takie jak martwe, śniegowe i wiatrowe, zgodnie z Sekcją 4.3.2 [1]. Wybór standardu "ASCE 7-16 NDS (Drewno)" w RFEM aktywuje opcję czasu trwania obciążenia w oknie dialogowym Przypadki obciążeń. Domyślne ustawienia klasy czasów trwania obciążenia (stałe, dziesięcioletnie itp.) są oparte na "Kategorii działania" przypadku obciążenia. Użytkownik może dostosować to ustawienie w RFEM lub RF-/TIMBER AWC. Wartość wybrana przez program opiera się na Tabeli 2.3.2 [1].

C_M – Współczynnik mokrej usługi

Uwzględnia warunki wpływu wilgoci na człon, jak określono w Sekcji 4.1.4 [1]. Użytkownik może wybrać "mokry" lub "suchy" w sekcji 'Warunki eksploatacyjne' RF-/TIMBER AWC.

C_t – Współczynnik temperatury

Uwzględnia narażenie na podwyższone temperatury do 100 stopni F, 100 do 125, i 125 do 150, jak opisano w Sekcji 2.3.3 [1]. Użytkownik może wybrać pomiędzy trzema zakresami temperatur w sekcji "Warunki eksploatacyjne" RF-/TIMBER AWC. Wartość wybrana przez program opiera się na Tabeli 2.3.3 z [1].

C_i – Współczynnik nacinania

Uwzględnia utratę powierzchni z drobnych nacięć wykonanych na członie w celu zastosowania środka konserwującego zapobiegającego rozkładowi, jak opisano w Sekcji 4.3.8 [1]. Użytkownik może wybrać "Nacięty" lub "Nie nacięty" w sekcji "Dodatkowe parametry projektowe" RF-/TIMBER AWC.

C_r – Współczynnik powtarzalnych członów

Jest używany, gdy wiele członów działa kompozytowo, aby właściwie rozdzielić obciążenie między sobą, jak opisano w Sekcji 4.3.9 [1]. C_r = 1.15 dla członów, które spełniają kryteria bliskiej odległości i połączenia przez osłonę lub równoważną. Użytkownik może wybrać "Nie powtarzalny" lub "Powtarzalny" w sekcji "Dodatkowe parametry projektowe" RF-/TIMBER AWC.

Uwaga: Jeśli to konieczne, wartości standardowe współczynników korekcyjnych wprowadzonych przez użytkownika mogą być zmieniane w opcji "Standard".

Możliwość zastosowania współczynników korygujących

Czynniki wykluczone w programie

C_T – Współczynnik sztywności wyboczeniowej

Uwzględnia wkład osłon ze sklejki do odporności na wyboczenie członów kratownicy w kompresji, jak określono w Sekcji 4.4.2 [1]. Ten współczynnik jest używany do zwiększania E_min członu. C_T można obliczyć ręcznie zgodnie z Równaniem 4.4-1 [1], lub zachowawczo przyjąć jako 1.0.

C_b – Współczynnik powierzchni łożyskowej

Jest używany do zwiększania wartości projektowych w kompresji (F_cp) dla skoncentrowanych obciążeń przykładanych prostopadle do słojów, jak określono w Sekcji 3.10.4 [1]. C_b można obliczyć ręcznie zgodnie z równaniem 3.10-2 [1], lub zachowawczo przyjąć jako 1.0.

Rzeczywiste naprężenia w belce-kolumnie

W tym przykładzie kombinacja obciążenia została uproszczona do CO1: DL + SL + WL.

• Naprężenie w kompresji od obciążeń stałych i śniegowych, f_c = 171 psi
• Naprężenie zginające osi silnej od obciążenia wiatrem, f_bx = f_b1 = 353 psi
• Naprężenie zginające osi słabej od obciążeń stałych i śniegowych, f_by = f_b2 = 1,029 psi

Określenie skorygowanych wartości projektowych zgodnie z Tabelą 4.3.1 NDS 2018 metodą ASD

• Krytyczna wartość projektowa wyboczenia dla członu w kompresji w osi silnej, F_cEx:
  $${\mathrm{F}}_{\mathrm{cEx}} = {\mathrm{F}}_{\mathrm{cE}1} = \frac{0.822 · {\mathrm{E}}_{\min }\text{'}}{{\left[{\displaystyle \frac{{\mathrm{l}}_{\mathrm{e}1}}{{\mathrm{d}}_1}}\right]}^2}$$

  $${\mathrm{F}}_{\mathrm{cEx}} = {\mathrm{F}}_{\mathrm{cE}1} = \frac{0.822 · 510,000 \mathrm{psi}}{{\left[{\displaystyle \frac{36.0 \mathrm{in}}{3.5 \mathrm{in}}}\right]}^2}$$

  $${\mathrm{F}}_{\mathrm{cEx}} = {\mathrm{F}}_{\mathrm{cE}1} = 3,963 \mathrm{psi}$$

  FcEx	Critical buckling design value for the compression member in the major axis, psi
  Emin'	= Emin ⋅ CM ⋅ CT ⋅ Ci = 510,000 psi
  le1	Effective length = 36.0 in
  d1	Member depth = 3.5 in

  Krytyczna wartość obliczeniowa wyboczenia dla pręta ściskanego w osi mocnej, FcEx
• Krytyczna wartość projektowa wyboczenia dla członu w kompresji w osi słabej, F_cEy:
  $${\mathrm{F}}_{\mathrm{cEy}} = {\mathrm{F}}_{\mathrm{cE}2} = \frac{0.822 · {\mathrm{E}}_{\min }\text{'}}{{\left[{\displaystyle \frac{{\mathrm{l}}_{\mathrm{e}2}}{{\mathrm{d}}_2}}\right]}^2}$$

  $${\mathrm{F}}_{\mathrm{cEy}} = {\mathrm{F}}_{\mathrm{cE}2} = \frac{0.822 · 510,000 \mathrm{psi}}{{\left[{\displaystyle \frac{36.0 \mathrm{in}}{1.5 \mathrm{in}}}\right]}^2}$$

  $${\mathrm{F}}_{\mathrm{cEy}} = {\mathrm{F}}_{\mathrm{cE}2} = 728 \mathrm{psi}$$

  FcEy	Critical buckling design value for the compression member in the minor axis, psi
  Emin'	= Emin ⋅ CM ⋅ CT ⋅ Ci = 510,000 psi
  le2	Effective length = 36.0 in
  d2	Member thickness = 1.5 in

  Krytyczna wartość obliczeniowa wyboczenia dla pręta ściskanego względem osi słabej, FcEy
• Skorygowana wartość projektowa kompresji równolegle do włókien, F_c':
  $${\mathrm{F}}_{\mathrm{c}}\text{'} = {\mathrm{F}}_{\mathrm{cy}}\text{'} = {\mathrm{F}}_{\mathrm{c}} · {\mathrm{C}}_{\mathrm{D}} · {\mathrm{C}}_{\mathrm{M}} · {\mathrm{C}}_{\mathrm{t}} · {\mathrm{C}}_{\mathrm{F}} · {\mathrm{C}}_{\mathrm{i}} · {\mathrm{C}}_{\mathrm{P}}$$

  $${\mathrm{F}}_{\mathrm{c}}\text{'} = {\mathrm{F}}_{\mathrm{cy}}\text{'} = 1,450 \mathrm{psi} · 1.6 · 1.0 · 1.0 · 1.0 · 1.0 · 0.29$$

  $${\mathrm{F}}_{\mathrm{c}}\text{'} = {\mathrm{F}}_{\mathrm{cy}}\text{'} = 673 \mathrm{psi}$$

  Fc'	Adjusted compressive design value parallel to the grain, psi
  Fc	Reference compressive design values parallel to the grain, psi
  CD	Load duration factor
  CM	Wet service factor
  Ct	Temperature factor
  CF	Size factor
  Ci	Incising factor
  CP	Column stability factor

  Skorygowana wartość obliczeniowa ściskania w kierunku włókien, Fc '
• Krytyczna wartość projektowa wyboczenia dla członu zginającego, F_bE:
  $${\mathrm{F}}_{\mathrm{bE}} = \frac{1.20 · {\mathrm{E}}_{\min }\text{'}}{{{\mathrm{R}}_{\mathrm{B}}}^2}$$

  $${\mathrm{F}}_{\mathrm{bE}} = \frac{1.20 · 510,000 \mathrm{psi}}{{9.65}^2}$$

  $${\mathrm{F}}_{\mathrm{bE}} = 6,577 \mathrm{psi}$$

  FbE	Critical buckling design value for the bending member, psi
  Emin'	= Emin ⋅ CM ⋅ CT ⋅ Ci = 510,000 psi
  RB	Slenderness ratio = 9.65 < 50 (NDS Equation 3.3-5)

  Krytyczna obliczeniowa wartość wyboczenia dla pręta zginanego, FbE
• Skorygowana wartość projektowa zginania osi silnej, F_bx':
  $${\mathrm{F}}_{\mathrm{bx}}\text{'}= {\mathrm{F}}_{\mathrm{b}1} = {\mathrm{F}}_{\mathrm{b}} · {\mathrm{C}}_{\mathrm{D}} · {\mathrm{C}}_{\mathrm{M}} · {\mathrm{C}}_{\mathrm{L}} · {\mathrm{C}}_{\mathrm{t}} · {\mathrm{C}}_{\mathrm{F}} · {\mathrm{C}}_{\mathrm{i}} · {\mathrm{C}}_{\mathrm{r}}$$

  $${\mathrm{F}}_{\mathrm{bx}}\text{'}= {\mathrm{F}}_{\mathrm{b}1} = 1,100 \mathrm{psi} · 1.6 · 1.0 · 0.982 · 1.0 · 1.0 · 1.0 · 1.0$$

  $${\mathrm{F}}_{\mathrm{bx}}\text{'}= {\mathrm{F}}_{\mathrm{b}1} = 1,729 \mathrm{psi}$$

  Fbx'	Adjusted major axis bending design value, psi
  Fb	Reference bending design value, psi
  CD	Load duration factor
  CM	Wet service factor
  CL	Beam stability factor
  Ct	Temperature factor
  CF	Size factor
  Ci	Incising factor
  Cr	Repetitive member factor

  Skorygowana wartość obliczeniowa zginania względem osi mocnej, Fbx'
• Skorygowana wartość projektowa zginania osi słabej, F_by':
  $${\mathrm{F}}_{\mathrm{by}}\text{'} = {\mathrm{F}}_{\mathrm{b}2} = {\mathrm{F}}_{\mathrm{b}} · {\mathrm{C}}_{\mathrm{D}} · {\mathrm{C}}_{\mathrm{M}} · {\mathrm{C}}_{\mathrm{L}} · {\mathrm{C}}_{\mathrm{t}} · {\mathrm{C}}_{\mathrm{fu}} · {\mathrm{C}}_{\mathrm{F}} · {\mathrm{C}}_{\mathrm{i}} · {\mathrm{C}}_{\mathrm{r}}$$

  $${\mathrm{F}}_{\mathrm{by}}\text{'} = {\mathrm{F}}_{\mathrm{b}2} = 1,100 \mathrm{psi} · 1.6 · 1.0 · 1.0 · 1.0 · 1.1 · 1.0 · 1.0 · 1.0$$

  $${\mathrm{F}}_{\mathrm{by}}\text{'} = {\mathrm{F}}_{\mathrm{b}2} = 1,936 \mathrm{psi}$$

  Fby'	Adjusted minor axis bending design value, psi
  Fb	Reference bending design value, psi
  CD	Load duration factor
  CM	Wet service factor
  CL	Beam stability factor
  Ct	Temperature factor
  Cfu	Flat use factor
  CF	Size factor
  Ci	Incising factor
  Cr	Repetitive member factor

  Skorygowana wartość obliczeniowa zginania względem osi słabej, Fby'
• Wskaźnik projektowania kombinowanego zginania dwuosiowego i kompresji osiowej

Wstawiając rzeczywiste naprężenia i ograniczające wartości projektowe przedstawione powyżej do równania NDS 3.9-3 [1], końcowy wskaźnik projektowania jest pokazany poniżej.

I równanie NDS 3.9-4 [1],

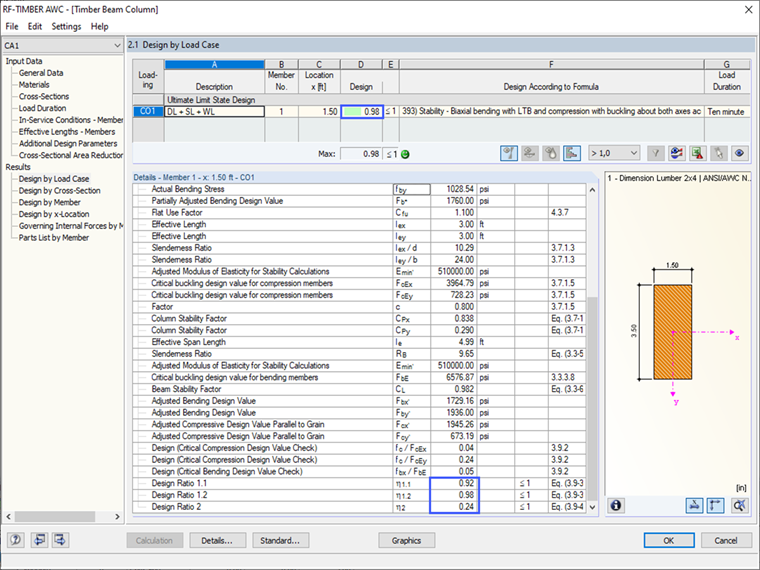
Wynik w RF-/TIMBER AWC

Użytkownik może porównać każdy współczynnik korekcyjny i skorygowaną wartość projektową z analitycznego ręcznego sposobu obliczeń do podsumowania wyników w RF-/TIMBER AWC. Jak pokazano, wyniki są identyczne. Kontrolujący końcowy wskaźnik projektowania = 0,98 jest oparty na metodzie obliczeniowej analizy geometrycznie liniowej (pierwszego stopnia). Należy pamiętać, że domyślne ustawienie w RFEM dla kombinacji obciążenia jest ustawione na analizę drugiego rzędu. To spowoduje nieco większy wskaźnik projektowy = 1,03. Użytkownik ma możliwość wyboru, która z metod wymienionych w "Parametrach obliczeniowych" jest najlepsza dla struktury.

Stopień wykorzystania

• 3D Viewer
• 3D Viewer | Babylon
• Wirtualna rzeczywistość

Słup z drewnianej belki