Description
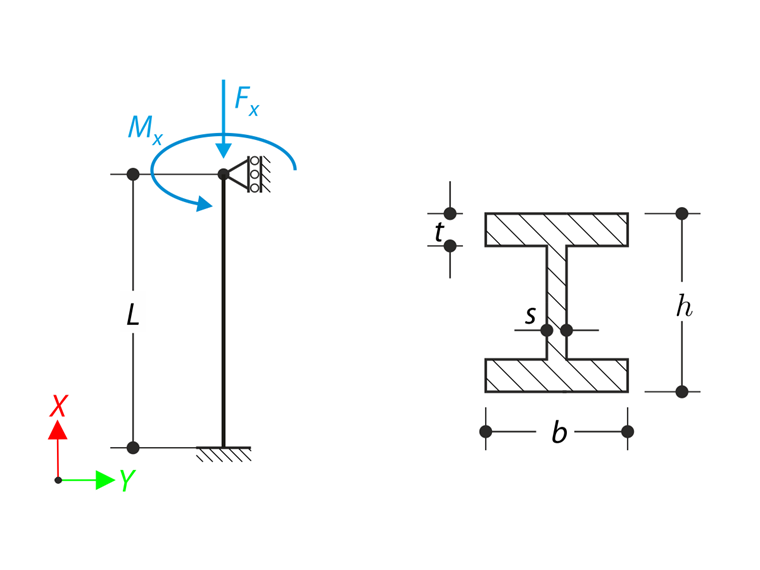
Member with the given boundary conditions is loaded with the moment M and the axial force Fx. Neglecting it's self-weight, determine beam's maximum torsional deformation φx,max as well as its inner torsional moment MT defined as a sum of a primary torsional moment MTpri and torsional moment caused by the normal force MTN. Provide a comparison of those values while assuming or neglecting the influence of the normal force. The verification example is based on the example introduced by Gensichen and Lumpe (see the reference).
| Material | Steel | Modulus of Elasticity | E | 210000.000 | MPa |
| Shear Modulus | G | 81000.000 | MPa | ||
| Geometry | Beam | Length | L | 3.000 | m |
| Height | h | 0.400 | m | ||
| Width | b | 0.180 | m | ||
| Web Thickness | s | 0.010 | m | ||
| Flange Thickness | t | 0.014 | m | ||
| Load | Torsional Moment | M | 1.200 | kNm | |
| Axial Force | Fx | 500.000 | kN | ||
Analytical Solution
Assuming that the relative torsion φ' is constant and no secondary torsional moment acts on the structure, beam's torsional moment MT can be obtained as a sum of a primary torsional moment MTpri and torsional moment caused by the normal force MTN.
where
Torsional moment equals to the acting moment (MT=M) and the normal force has the opposite value of the acting force (N=-Fx), beam's relative torsion φ' can be expressed as follows:
Maximum torsional deformation at the end of the beam φx,max can be calculated as follows:
RFEM Settings
- Modeled in version RFEM 5.03 and RFEM 6.01
- The element size is lFE= 0.300 m
- The number of increments is 1
- The element type is member
- Isotropic linear elastic material model is used
- Shear stiffness of members is activated
Results
| φx,max [rad] | Analytical Solution | RFEM 6 | Ratio | RFEM 5 - RF-FE-LTB | Ratio |
| N = 0 kN | 0.101 | 0.101 | 1.000 | 0.101 | 1.000 |
| N = -500 kN | 0.166 | 0.165 | 0.994 | 0.165 | 0.994 |
| MTpri [kNm] | Analytical Solution | RFEM 6 | Ratio | RFEM 5 - RF-FE-LTB | Ratio |
| N = 0 kN | 1.200 | 1.200 | 1.000 | 1.200 | 1.000 |
| N = -500 kN | 1.972 | 1.966 | 0.997 | 1.966 | 0.997 |
| MTN [kNm] | Analytical Solution | RFEM 6 | Ratio | RFEM 5 - RF-FE-LTB | Ratio |
| N = 0 kN | 0.000 | 0.000 | - | 0.000 | - |
| N = -500 kN | -0.772 | -0.766 | 0.992 | -0.766 | 0.992 |
| MT [kNm] | Analytical Solution | RFEM 6 | Ratio | RFEM 5 - RF-FE-LTB | Ratio |
| N = 0 kN | 1.200 | 1.200 | 1.000 | 1.200 | 1.000 |
| N = -500 kN | 1.200 | 1.200 | 1.000 | 1.200 | 1.000 |
,_LC1__LI.jpg?mw=760&hash=4ae6f46d88e29447308efc0bce357f616d88671c)
,_LC1__LI.jpg?mw=350&hash=b3482f816b157606c7c88c75bfa2b52c5a8deab0)
,_LC1__LI.jpg?mw=350&hash=80caf81f6c0a20df0f1d44557864ff0117ccdd28)
