Opis prac
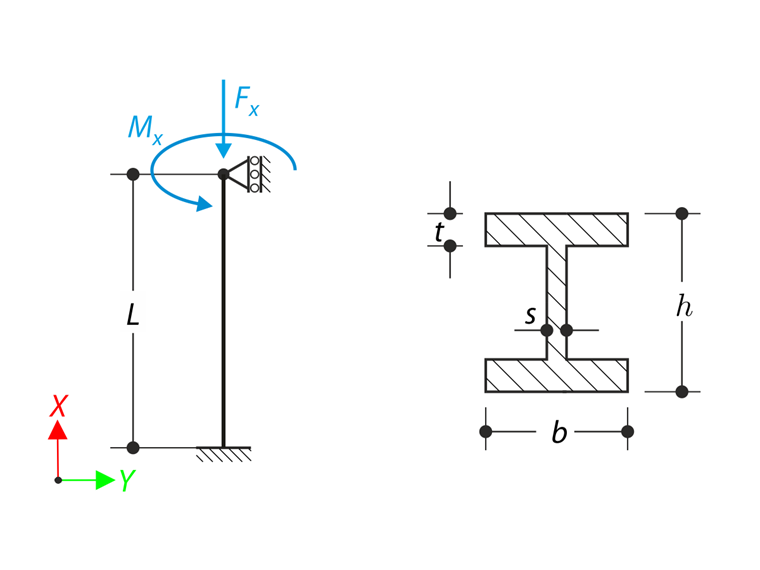
Pręt o zadanych warunkach brzegowych jest obciążony momentem M i siłą osiową Fx. Pomijając ciężar własny', należy określić maksymalne odkształcenie skrętne belki φx,max oraz jej wewnętrzny moment skręcający MT zdefiniowany jako suma pierwotnego momentu skręcającego MTpri i momentu skręcającego wywołanego siłą normalną siła MTN. Należy porównać te wartości, przyjmując lub pomijając wpływ siły normalnej. Przykład obliczeniowy oparty jest na przykładzie opracowanym przez Gensichen i Lumpe (patrz odnośnik).
| Materiał | Stal | Moduł sprężystości | E | 210000,000 | MPa |
| Moduł ścinania | [SCHOOL.NUMBEROFSINGLEUSERLICENCES] | 81000,000 | MPa | ||
| Geometria | Belka | obwiednia | [CONTACT.E-MAIL-SALUTATION] | 3,000 | m |
| Wysokość | H | 0,400 | m | ||
| Szerokość | b | 0,180 | m | ||
| Grubość środnika | s | 0,010 | m | ||
| Grubość półki | t | 0,014 | m | ||
| Obciążenie | moment skręcający | M | 1,200 | kNm | |
| siła osiowa | Fx | 500,000 | kN |
Rozwiązanie analityczne
Zakładając, że skręcanie względne φ' jest stałe i na konstrukcję nie działa drugorzędny moment skręcający, moment skręcający belki's MT można obliczyć jako sumę głównego momentu skręcającego MTpri i momentu skręcającego wywołanego siła MTN.
Gdzie
Moment skręcający jest równy momentowi działającemu (MT =M), a siła normalna ma wartość przeciwną do siły (N=-Fx ), względny skręcanie belki φ' można wyrazić w następujący sposób:
Maksymalne odkształcenie skrętne na końcu belki φx,max można obliczyć w następujący sposób:
Ustawienia RFEM
- Modelowany w wersji RFEM 5.03 i RFEM 6.01
- Rozmiar elementu wynosi lFE = 0,300 m
- Liczba przyrostów wynosi 1
- Typ elementu to pręt
- Zastosowano izotropowy liniowo sprężysty model materiałowy
- Sztywność prętów na ścinanie jest aktywowana
Wyniki
| φx,max [rad] | Rozwiązanie analityczne | RFEM 6 | Stosunek | RFEM 5 - RF-FE-LTB | Stosunek |
| N = 0 kN | 0,101 | 0,101 | 1,000 | 0,101 | 1,000 |
| N = -500 kN | 0,166 | 0,165 | 0,994 | 0,165 | 0,994 |
| MTpri [kNm] | Rozwiązanie analityczne | RFEM 6 | Stosunek | RFEM 5 - RF-FE-LTB | Stosunek |
| N = 0 kN | 1,200 | 1,200 | 1,000 | 1,200 | 1,000 |
| N = -500 kN | 1,972 | 1,966 | 0,997 | 1,966 | 0,997 |
| [kNm ] | Rozwiązanie analityczne | RFEM 6 | Stosunek | RFEM 5 - RF-FE-LTB | Stosunek |
| N = 0 kN | 0,000 | 0,000 | - | 0,000 | - |
| N = -500 kN | -0,772 | -0,766 | 0,992 | -0,766 | 0,992 |
| MT [kNm] | Rozwiązanie analityczne | RFEM 6 | Stosunek | RFEM 5 - RF-FE-LTB | Stosunek |
| N = 0 kN | 1,200 | 1,200 | 1,000 | 1,200 | 1,000 |
| N = -500 kN | 1,200 | 1,200 | 1,000 | 1,200 | 1,000 |
,_LC1__LI.jpg?mw=760&hash=4ae6f46d88e29447308efc0bce357f616d88671c)
,_LC1__LI.jpg?mw=350&hash=b3482f816b157606c7c88c75bfa2b52c5a8deab0)
,_LC1__LI.jpg?mw=350&hash=80caf81f6c0a20df0f1d44557864ff0117ccdd28)
