Beschreibung
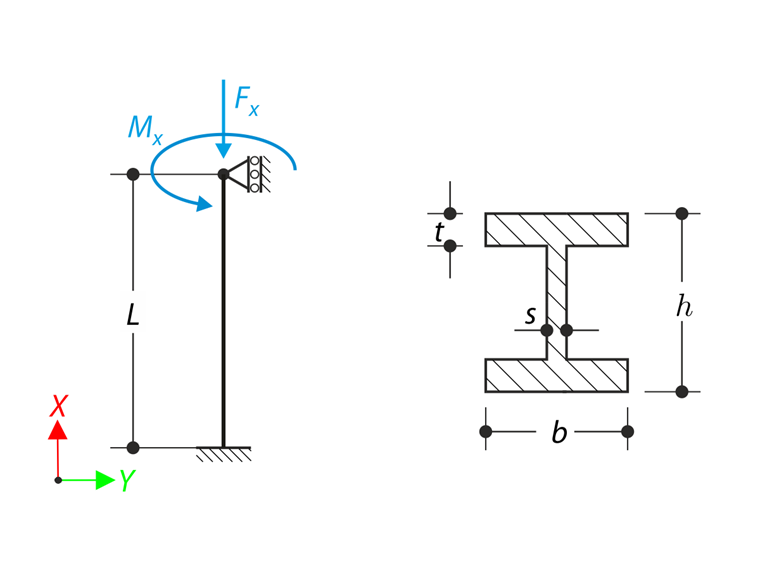
Ein Stab mit den festgelegten Randbedingungen wird mit einem Moment M und einer Normalkraft Fx belastet. Bestimmen Sie dessen maximale Torsionsverformung φx,max sowie sein inneres Torsionsmoment MT, das als Summe eines primären Torsionsmoments MTpri und eines durch Normalkraft verursachten Torsionsmoments definiert ist, wobei sein Eigengewicht nicht zu berücksichtigen ist Kraft MTN. Vergleichen Sie diese Werte, während Sie den Einfluss der Normalkraft annehmen oder nicht berücksichtigen. Dieses Verifikationsbeispiel basiert auf dem von Gensichen und Lumpe vorgestellten Beispiel (siehe Literatur).
| Material | Stahl | Elastizitätsmodul | E | 210000,000 | MPa |
| Schubmodul | G | 81000,000 | MPa | ||
| Geometrie | Balken | Länge | L | 3,000 | m |
| Höhe | h | 0.400 | m | ||
| Breite | F | 0,180 | m | ||
| Stegdicke | S | 0.010 | m | ||
| Flanschdicke | t | 0,014 | m | ||
| Last | Torsionsmoment | M | 1.200 | kNm | |
| Normalkraft | Fx | 500,000 | kN | ||
Analytische Lösung
Unter der Annahme, dass die bezogene Torsion φ' konstant ist und kein sekundäres Torsionsmoment auf das Tragwerk wirkt, kann das Torsionsmoment MT des Trägers' als Summe des primären Torsionsmoments MTpri und des durch die Normale verursachten Torsionsmoments erhalten werden Kraft MTN.
mit
Torsionsmoment gleich dem einwirkenden Moment (MT =M) und die Normalkraft den entgegengesetzten Wert der einwirkenden Kraft hat (N=-Fx ), lässt sich die relative Torsion des Trägers φ' wie folgt ausdrücken:
Die maximale Torsionsverformung am Ende des Trägers φx,max kann wie folgt berechnet werden:
RFEM-Einstellungen
- Modelliert in Version RFEM 5.03 und RFEM 6.01
- Die Elementgröße beträgt lFE = 0,300 m
- Die Anzahl der Stufen ist 1
- Der Elementtyp ist ein Stab
- Es wird ein isotropes linear-elastisches Materialmodell vorausgesetzt.
- Schubsteifigkeit der Stäbe ist aktiviert
Ergebnisse
| φx,max [rad] | Analytische Lösung | RFEM 6 | Verhältnis | RFEM 5 - RF-FE-BGDK | Verhältnis |
| N = 0 kN | 0,101 | 0,101 | 1,000 | 0,101 | 1,000 |
| N = -500 kN | 0,166 | 0,165 | 0,994 | 0,165 | 0,994 |
| MTpri [kNm] | Analytische Lösung | RFEM 6 | Verhältnis | RFEM 5 - RF-FE-BGDK | Verhältnis |
| N = 0 kN | 1.200 | 1.200 | 1,000 | 1.200 | 1,000 |
| N = -500 kN | 1,972 | 1,966 | 0,997 | 1,966 | 0,997 |
| MTN [kNm] | Analytische Lösung | RFEM 6 | Verhältnis | RFEM 5 - RF-FE-BGDK | Verhältnis |
| N = 0 kN | 0,000 | 0,000 | |||
| 0,000 | |||||
| N = -500 kN | -0,772 | -0,766 | 0,992 | -0,766 | 0,992 |
| MT [kNm] | Analytische Lösung | RFEM 6 | Verhältnis | RFEM 5 - RF-FE-BGDK | Verhältnis |
| N = 0 kN | 1.200 | 1.200 | 1,000 | 1.200 | 1,000 |
| N = -500 kN | 1.200 | 1.200 | 1,000 | 1.200 | 1,000 |
,_LC1__LI.jpg?mw=760&hash=4ae6f46d88e29447308efc0bce357f616d88671c)
,_LC1__LI.jpg?mw=350&hash=b3482f816b157606c7c88c75bfa2b52c5a8deab0)
,_LC1__LI.jpg?mw=350&hash=80caf81f6c0a20df0f1d44557864ff0117ccdd28)
