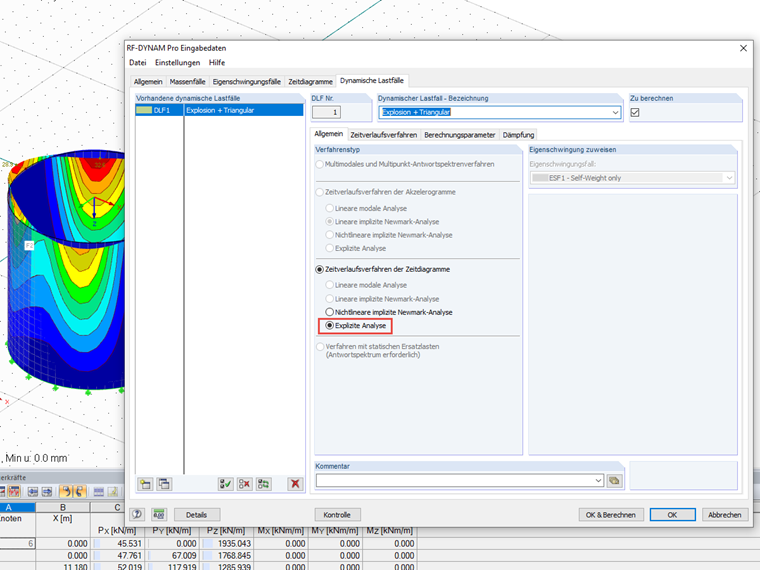
The RF‑DYNAM Pro – Nonlinear Time History offers an implicit NEWMARK solver of the method of mean acceleration, as well as an explicit solver.
It should be noted that the "original" version of the central difference method is not used here, but a modified form. The modification is characterized by the fact that the applied velocity difference is not a central difference. The following two equations show the applied differences in velocity and acceleration:
This approach leads to a faster convergence since it responds "faster" to changes in loading or structure (nonlinearities). FAQ 2356 describes in detail when the explicit analysis should be selected.