Answer:
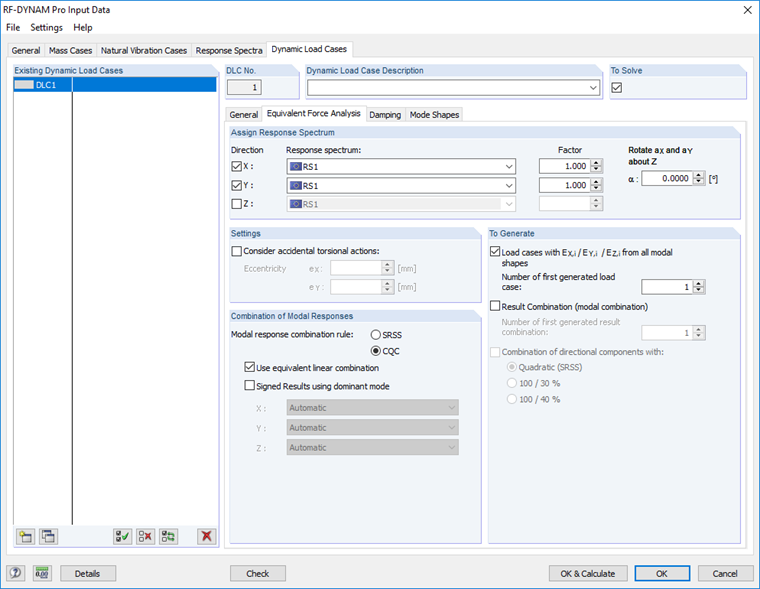
The complete quadratic combination (CQC) rule must be applied when analyzing spatial models with combined torsional/translational eigenmodes that have adjacent modal shapes whose periods differ by less than 10%. If this is not the case, the square root of the sum of the squares (SRSS rule) applies. In all other cases, the CQC rule must be applied. The CQC rule is defined as follows:
with the correlation coefficient:
| Di, Dj | Damping values |
| r | Quotient of the natural angular frequencies (ωj/ ωi) |
The correlation coefficient is simplified if the viscous damping value D is selected to be the same for all mode shapes:
| D | Damping value |
| r | Quotient of the natural angular frequencies (ωj/ ωi) |
By analogy to the SRSS rule, the CQC rule can also be performed as an equivalent linear combination. The formula of the modified CQC rule is as follows:
