Back to FAQ
Is this page helpful?
1127x
004829
Sonja von Bloh, M.Sc.
2020-11-20

Load Distribution on Members for Angular Axis Method

How is the load distributed to the members in the angular axis method if the members are excluded from the load application?

Answer:

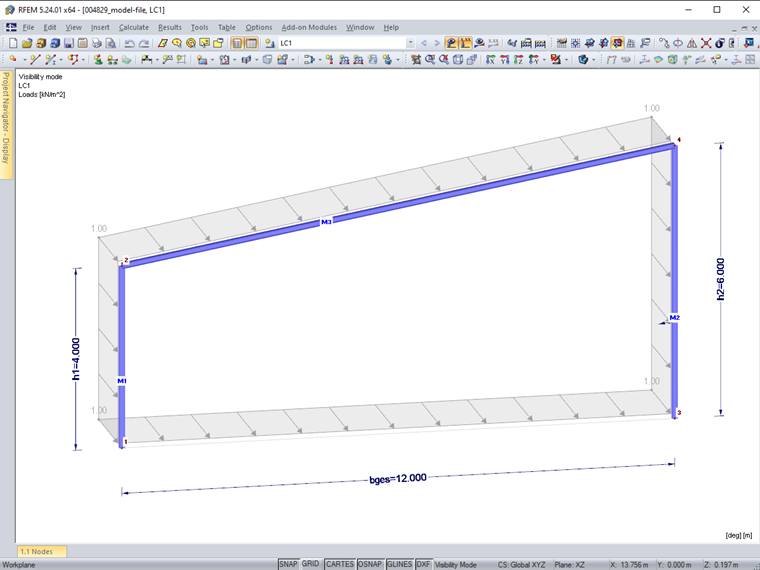
An area load of 1 kN/m² delimited by Node 1 to Node 4 is only applied to Member 3 (Image 01).

Surface Load
1 Surface Load

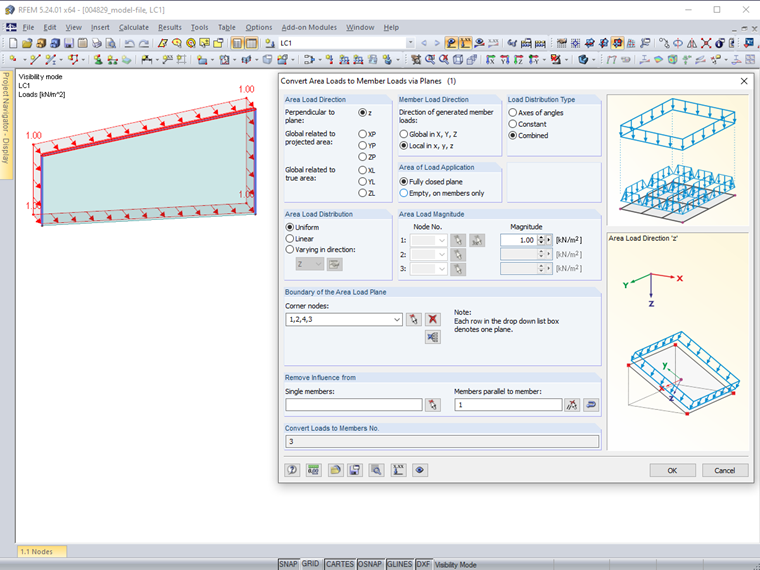
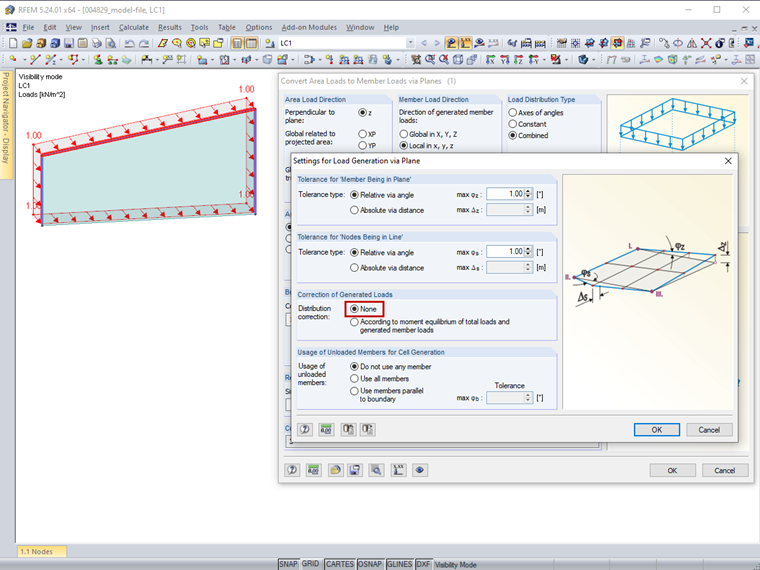
The entries carried out in the load generator are shown in Image 02. There is no correction of the distribution according to the moment equilibrium (Image 03).

Settings for Converting Surface Loads to Member Loads
2 Settings for Converting Surface Loads to Member Loads

Settings for Load Generation via Plane
3 Settings for Load Generation via Plane

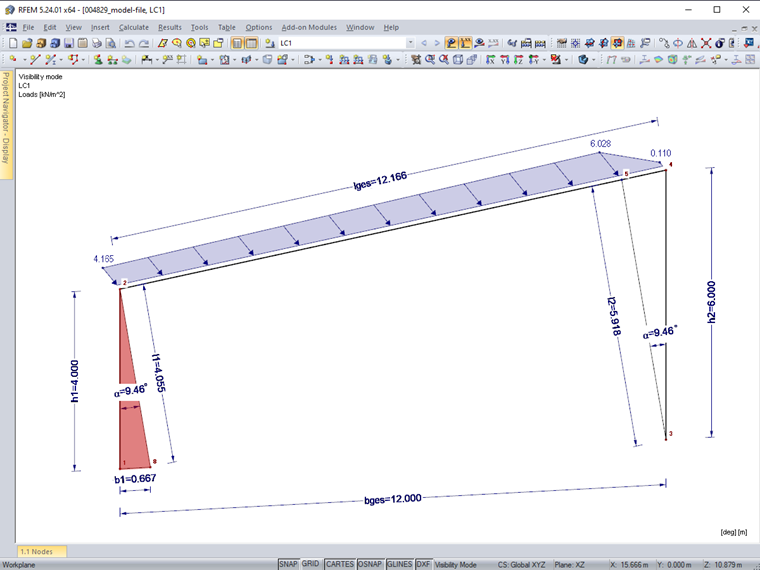
The generated member load is shown in Image 04. This is calculated as follows:

q = 1.00 kN/m2
h1 = 4.00 m
h2 = 6.00 m
btot = 12.00 m
α =arctan h2 - h1btot = arctan 6.000 - 4.00012.000 = 9.46°
b1 = tan (α) ⋅ h1 = tan (9.46°) ⋅ 4.000 = 0.667 m
l1 = b12 + h12 = 0.6672 + 4.0002 = 4.055 m
l2 = cos (α) ⋅ h2 = cos (9.46°) ⋅ 6.000 = 5.918 m
AR = b1 · h12= 0.667 · 4.0002 = 1.335 m2
ltot = btot2 + h2-h12 = 12.0002 + 6.000-4.0002 = 12.166 m

q

Lastgröße Flächenlast

AR

Restfläche (im Bild 4 rot markiert)

qc

konstanter Lastanteil auf belasteten Stab

q2

Stablast Knoten 2

q5

Stablast Knoten 5

q4

Stablast Knoten 4
Calculation of Member Load

Generated Member Load from Surface Load
4 Generated Member Load from Surface Load

Author

Ms. von Bloh provides technical support for our customers and is responsible for the development of the SHAPE‑THIN program as well as steel and aluminum structures.

Downloads
RFEM Model File
456 KB
  • Mia: AI Assistant
  • Latest FAQ
Events
Videos
Models to Download
Knowledge Base Articles
Model showing integrated steel joints highlighting connection and structure interaction in design.
This article explores the importance of considering joint-structure interaction in modeling and design and how to do it in RFEM 6.
Illustration of equivalent lateral force method for seismic analysis in structural engineering
This article provides a comprehensive overview of essential seismic analysis methods, explaining their principles and applications, as well as the scenarios in which they are most effective
KB 001925 | AISC Fillet Weld Design in RFEM 6
The weld stresses between surfaces can be determined using the Stress-Strain Analysis add-on in RFEM 6. Furthermore, the stress limit determined according to the applicable standard can be input to determine the stress ratio of the weld. This article focuses on the fillet weld design according to AISC 360-22 [1] with two examples from AISC Volume 1: Design Examples [2].
Structural analysis of an end plate connection in Dlubal software
This article demonstrates how to initiate and conduct the analysis in the software, followed by a short discussion of the underlying concept.
Screenshots
Product Features
Feature 002916 | Joint-Structure Interaction for Steel Joints

Want to automatically consider steel joint stiffness in your global RFEM model? Utilize the Steel Joints add-on!

Activate joint-structure interaction in the stiffness analysis of your steel joints. Hinges with springs are then automatically generated in the global model and included in subsequent calculations.

Feature 002820 | Limit Plastic Strain for Welds

In the ultimate configuration of the steel joint design, you have the option to modify the limit plastic strain for welds.

Component "Base Plate"

The "Base Plate" component allows you to design base plate connections with cast-in anchors. In this case, plates, welds, anchorages, and steel-concrete interaction are analyzed.

Feature 002807 | 3D Display of FSM Results

In the "Edit Section" dialog box, you can display the buckling shapes of the Finite Strip Method (FSM) as a 3D graphic.

Frequently Asked Questions (FAQ)

In the Steel Joints add-on, I get high utilization ratios for preloaded bolts in the tension design. Where do these high utilization ratios come from and how can I evaluate the load-bearing reserves of the bolt?

How can treating a connection as fully rigid result in an uneconomical design?

Is it possible to consider shear panels and rotational restraints in the global calculation?
A steel joint in my model is non-designable. How can I get more information to find the cause?
I am calculating a column that is restrained at the base, held in the head in the X-direction, and can buckle in the Y-direction. I have set the effective lengths using nodal supports. In the design, the values of the effective lengths for the calculation are both the same L_ (cr, z) = L_ (cr, y) = 2.41 m. What am I doing wrong?
What is the Function of Chained Analysis Diagram?
Customer Projects