Depending on whether a web or a flange is concerned, the coefficient kc, which takes into account the influence of the stress distribution within the partial cross‑section, is determined as follows:
and
In the case of pure tensile stress, kc = 1 applies for the entire cross‑section as well as the individual partial cross‑sections.
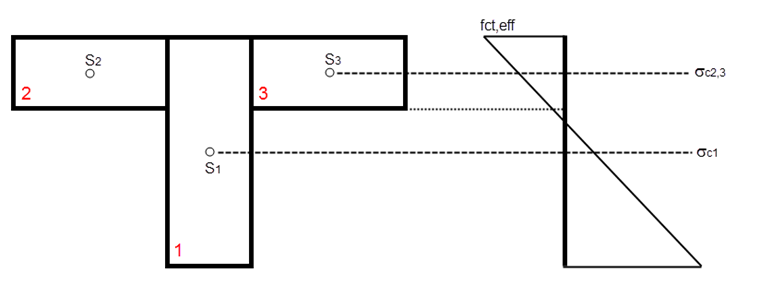
The mean concrete stress σc affecting the analyzed part of the cross‑section is determined using the concrete stress distribution, applying the crack moment due to fct,eff, in the centroid of the respective partial cross‑section (see Image 01 σc).
Options in RF-CONCRETE Members
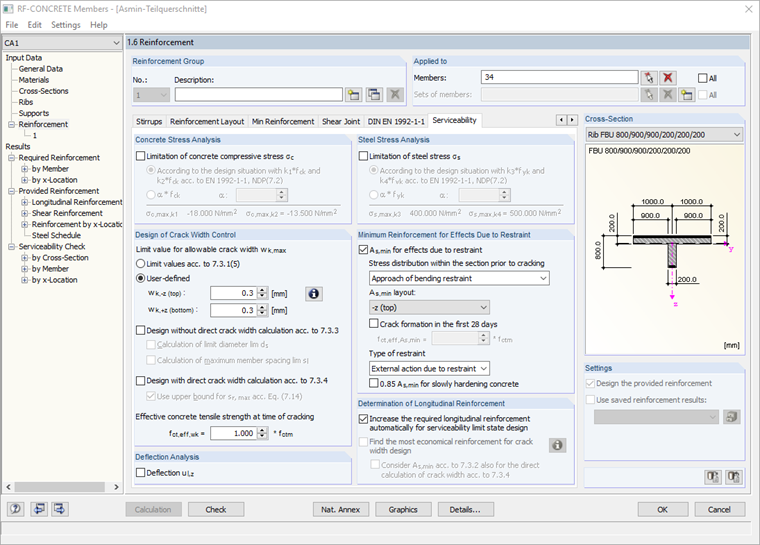
The partial cross‑sections are determined automatically, depending on the underlying cross‑section. The RF-CONCRETE Members add-on module provides the following control options, which have an effect on the minimum reinforcement of the partial cross-sections.
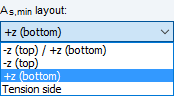
By selecting the minimum reinforcement layout, you specify at the same time on which side of the cross‑section the concrete tensile stress fct,eff is applied, or in which direction the crack moment acts.
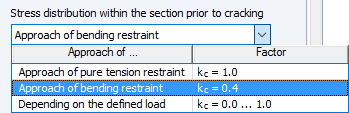
The corresponding options for stress distribution within the section prior to cracking control the distribution of the mean concrete stress.
If you select kc = 1.0, fct,eff is constantly applied over the cross‑section. If you select kc = 0.4 or kc = variable depending on the acting load, the distribution of the mean concrete stress is determined due to bending around y or due to bending around y and the axial force. The minimum reinforcement is arranged in the partial cross‑sections where the stress fct,eff is reached.
If fct,eff is not reached on any cross‑section fiber in some partial cross‑sections, nevertheless a wedge is formed; then the tensile force of the partial cross‑section is assigned to the governing tension side.
Results in RF-CONCRETE Members
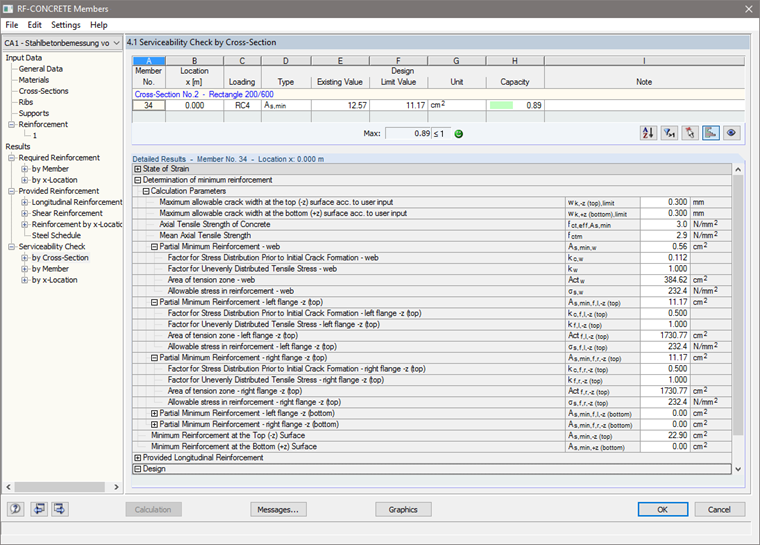
Window 4 shows the governing design and the detailed results of the minimum reinforcement for the individual partial cross-sections. For each partial cross‑section, the coefficient kc for considering the influence of the stress distribution, the area of the concrete tension zone Act, and the absolute value of the maximum allowable steel stress are displayed, among other results.
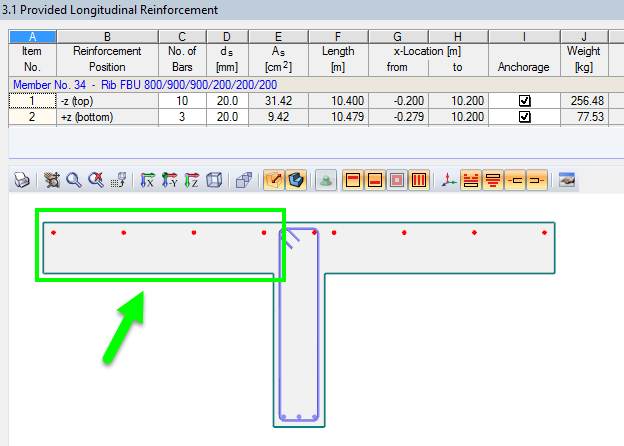
Under "Design", you can see the resulting design with the highest criterion. This is confronted with the calculated minimum reinforcement in the partial cross‑section of the provided reinforcement (Image 07).