Secondary Reinforcement According to DIN EN 1992-1-1 9.2.1 to Ensure Ductile Structural Component Behavior

By using the minimum reinforcement, the tensile stress, which was absorbed by the concrete before in the event of initial crack formation, should be covered by a reinforcement. This tensile stress can be described by the crack moment. The crack moment is the loading that generates a stress distribution in the considered cross-section, resulting in an initial crack formation. By arranging the minimum reinforcement, it should be ensured that the initial crack formation does not lead to failure of the component.

Determination of Minimum Reinforcement

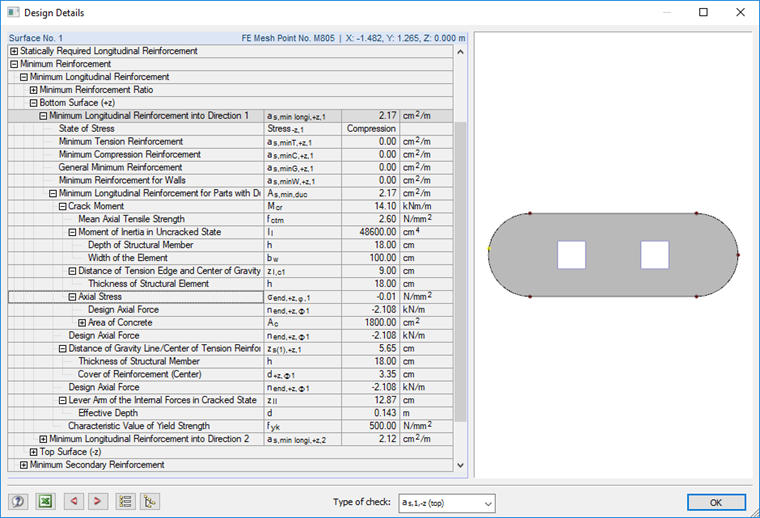
The crack moment M_cris determined as follows for a rectangular cross-section without axial force:

The minimum reinforcement for this loading results in:

Assuming that d ≈ 0.9 h and z ≈ 0.8 d, it follows:

The minimum reinforcement can be determined in general according to [2] as follows:

where
M_cr = cracking moment, for bending and longitudinal force
N = with N < 0 as compression force
f_ctm = mean tensile strength of concrete
f_yk = characterizes the value of the yield strength of reinforcement steel
S_c = section modulus of concrete cross-section in state I
A_c = surface of concrete cross-section in state I
z = lever arm of internal forces in state II
z_s1 = distance between centroidal axis minimum reinforcement and centroidal axis concrete cross-section

Specifics of Surface Design: RF-CONCRETE Surfaces

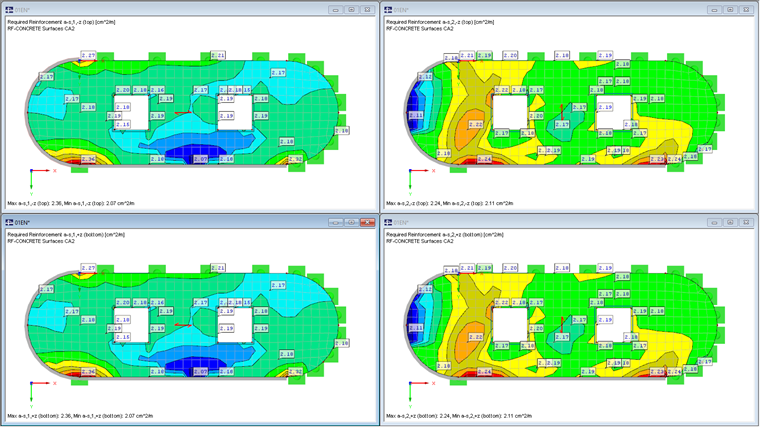
For the calculation in surfaces, the following particularity appears according to NCI on 9.3.1.1 (1): "For two-way slabs, the minimum reinforcement as in 9.2.1.1 (1) only needs to be arranged in the main span direction." Since the main direction does not have to run in one of the reinforcement directions, the minimum reinforcement will be arranged in the reinforcement direction nearest to the main direction. In this context, it may happen that the minimum reinforcement will be arranged partly in reinforcement direction 1 and partly in reinforcement direction 2.

For the "Reinforcement direction with the main tension force in the considered element" option, it is clearly shown in Figure 02 that the minimum reinforcement is only designed once per side and direction. This corresponds to the standard; it may, however, generate a reinforcement that seems unusual.

For a minimum reinforcement with a direction defined by the user, a more uniform image of the reinforcement distribution emerges. This can be seen clearly in Figure 04.

The intermediate values used in the calculation can be seen clearly in RF-CONCRETE Surfaces using the [Info] button in the calculation details.

Specifics of Member Design: RF-CONCRETE Members

In principle, the calculation of the secondary minimum reinforcement in RF-CONCRETE Members corresponds to the calculation in Surfaces. One particularity is that for members with segmented cross-sections, such as box sections or T-beams, the effective width for the determination of the crack moment has to be considered.