Consideration of Shear Stiffness for Cross-Section Calculation in RFEM 6

This article shows you the internal forces and displacements of a continuous beam calculated both with and without consideration of shear stiffness.

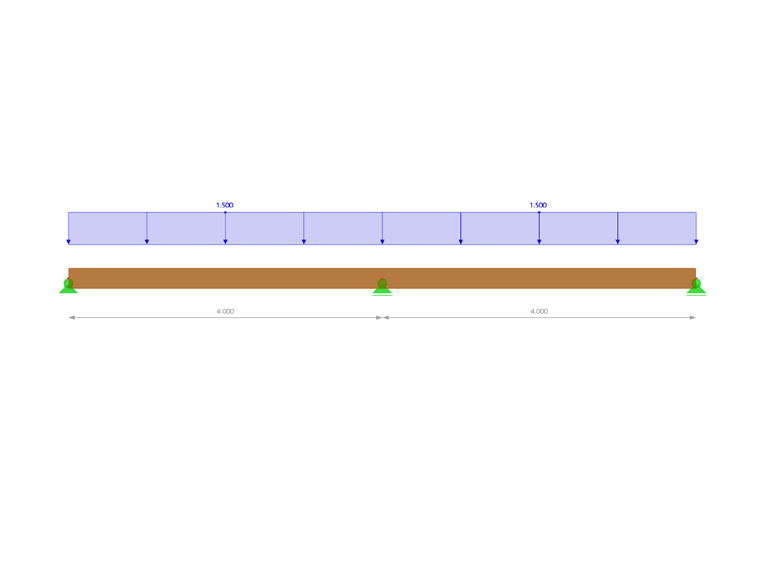
In RFEM 6, the shear stiffnesses of members are automatically considered by the program. However, this consideration leads to different results than those you might obtain with a manual calculation. To show this, as well as to illustrate how to deactivate the shear stiffness for a cross-section calculation, a practical example will be provided. The model of interest is a timber beam with two spans of 4 m each, loaded with 1.5 kN/m, as shown in Image 1.

1 Continuous Beam with Uniform Load

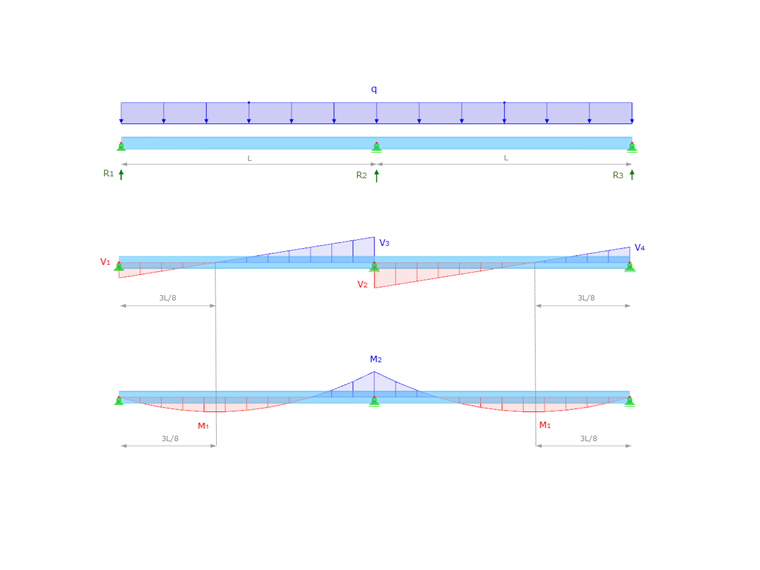
First, we can perform the manual calculation of internal forces and displacements for the continuous beam of interest. For this purpose, the available data can be entered into well-known beam design and deflection equations for a continuous beam with two equal spans and a uniformly distributed load. The distribution of internal forces is shown in Image 2, and the results obtained are as follows:

\frac{3 q L}{8} = \frac{3 * 1.5 * 4}{8} = 2.25 k N

Shear Force V₁ and V₄

\frac{5 q L}{8} = \frac{5 * 1.5 * 4}{8} = 3.75 k N

Shear Force V₂ and V₃

\frac{9 q L^{2}}{128} = \frac{9 * 1.5 * 4^{2}}{128} = 1.6875 k N m

Bending Moment M₁

\frac{q L^{2}}{8} = \frac{1.5 * 4^{2}}{8} = 3 k N m

Bending Moment M₂

Δ_{m a x} = \frac{q L^{4}}{185 E I} = \frac{1, 5 * 4^{4}}{185 * 2911.76} = 0.0007 m

Maximum Deflection Δ_max

2 Distribution of Internal Forces

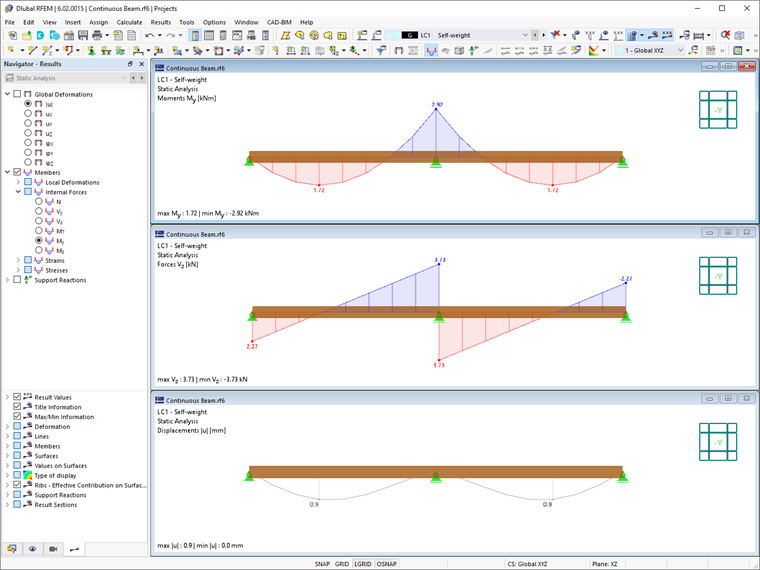
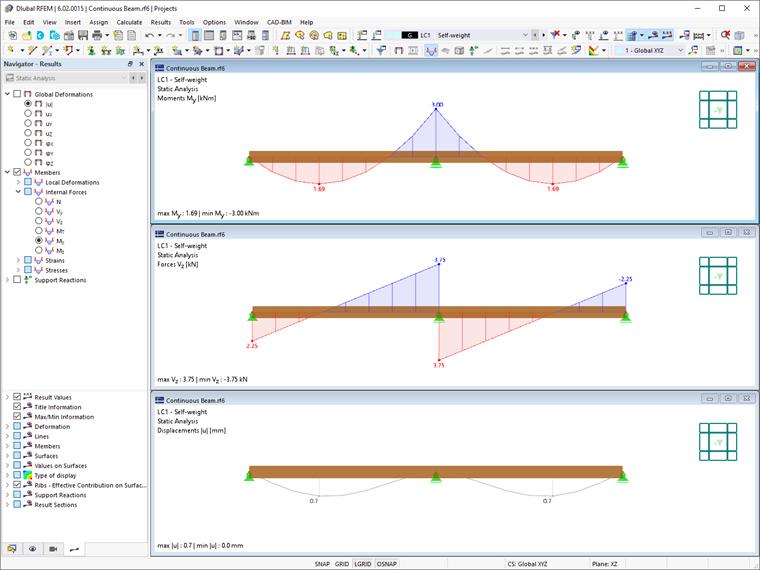
Next, you can perform the same calculation in RFEM 6 and look at the results obtained as shown in Image 3. As already mentioned, the difference with respect to the results of the manual calculation is due to the automatic consideration of the shear stiffness and the increased deformation.

3 Results with Consideration of Shear Stiffness

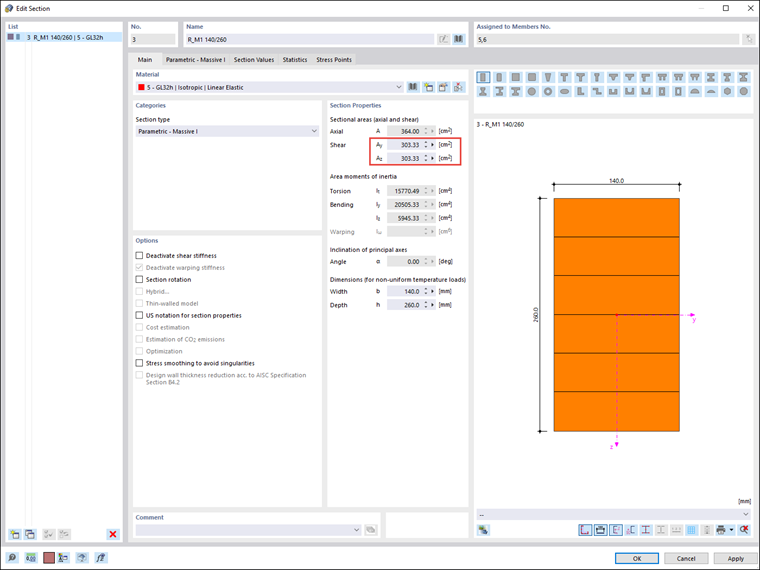
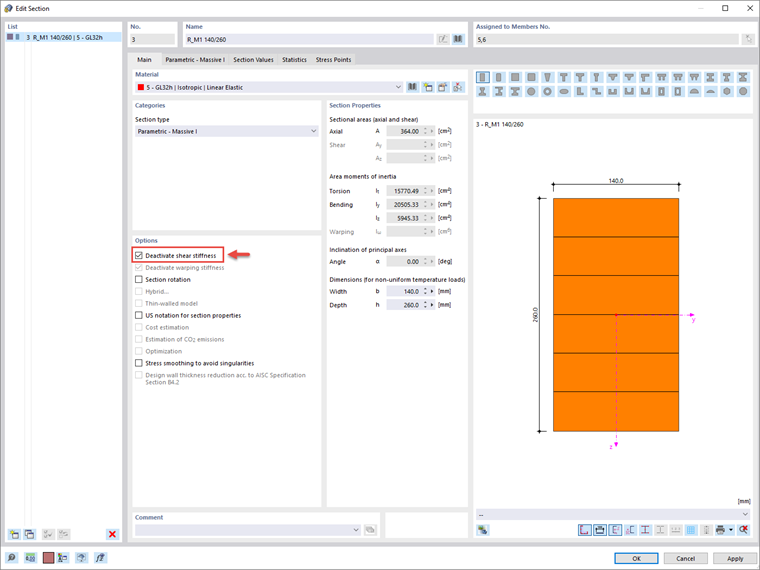
However, if you are interested in obtaining results for which the shear stiffness is not considered, this is also possible in RFEM 6 since you have the possibility to control the consideration of shear stiffnesses separately for each cross-section. To do so, you should open the associated "Edit Cross-Section" dialog box, as shown in Image 4. The influence of the shear depends on the cross-section areas A_y and A_z (Image 4).

These cross-section properties can be displayed in tables or cross-section entries and adjusted, if necessary. In addition, the shear stiffness can be deactivated (Image 5) and thus, not considered in the cross-section calculation. In this case, the results obtained in RFEM 6 (Image 6) will be identical to those calculated manually.