1003x

001866

Thomas Eichner, MSc.

22.12.2023

Détermination du coefficient de sensibilité pour étudier le besoin de théorie du second ordre pour les analyses dynamiques

Le coefficient de sensibilité du déplacement entre étages θ est fourni dans l’EN 1998-1, 2.2.2 et 4.4.2.2 afin d’évaluer s'il est également nécessaire de considérer l'analyse du second ordre dans une analyse dynamique. Il peut être calculé et analysé avec RFEM 6 et RSTAB 9.

Coefficient de sensibilité θ

Le coefficient de sensibilité θ est défini comme suit [1] :

θ = \frac{P_{tot} * d_{r}}{V_{tot} * h}

θ	Coefficient de la sensibilité du déplacement entre les étages
P_tot	Charge de gravité totale sur et au-dessus de l'étage considéré dans la situation de calcul sismique
d_r	le déplacement entre les étages de calcul déterminé comme la différence entre les déplacements latéraux moyens_ds entre le haut et le bas de l'étage concerné; dans ce cas, les déplacements sont déterminés à l'aide du spectre de réponse de calcul linéaire avec q = 1,0
V_tot	Effort tranchant sismique total déterminé à l'aide du spectre de réponse de calcul linéaire
h	Hauteur d'étage

Coefficient de sensibilité θ

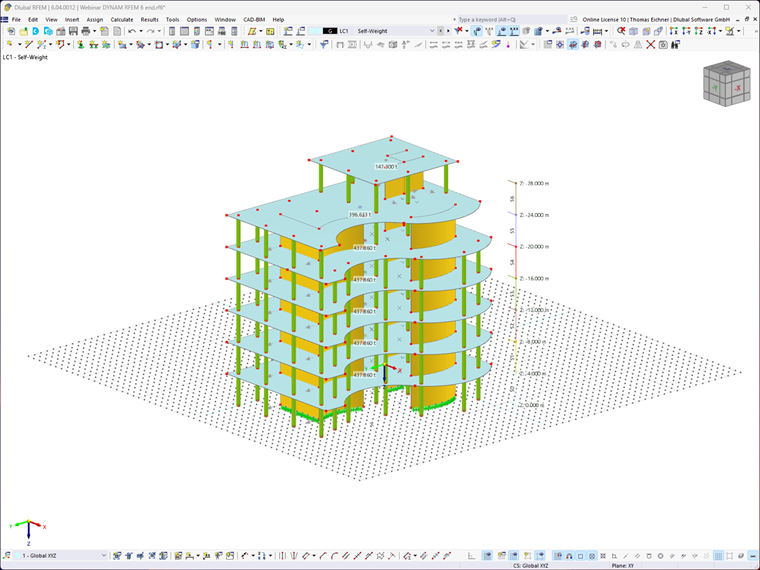
La procédure de calcul du coefficient de sensibilité est illustrée ci-dessous à l’aide de l’exemple d’un bâtiment en béton armé avec un rez-de-chaussée et six étages.

Vue d’ensemble du bâtiment

Pour calculer le coefficient de sensibilité, des additions sont utilisées :

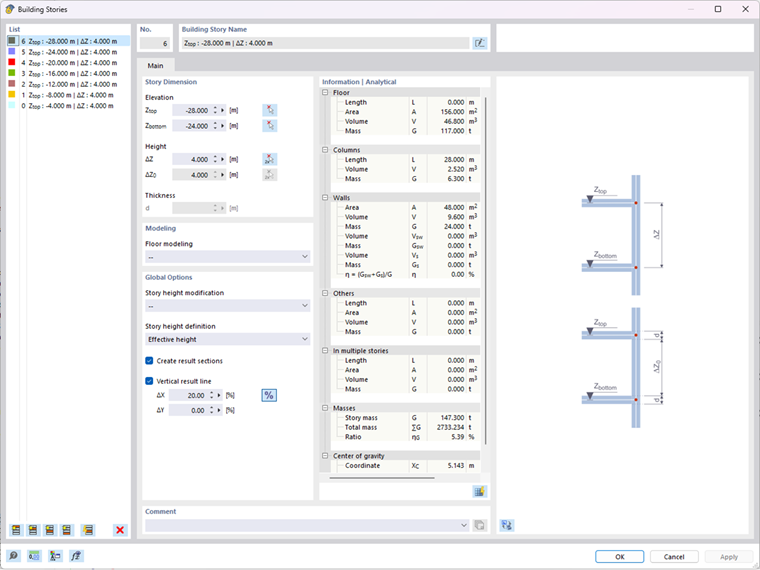
Après avoir modélisé le bâtiment, les étages doivent être définis à l’aide du module complémentaire Modèle de bâtiment.

Définition de l’étage à l’aide du module complémentaire Modèle de bâtiment

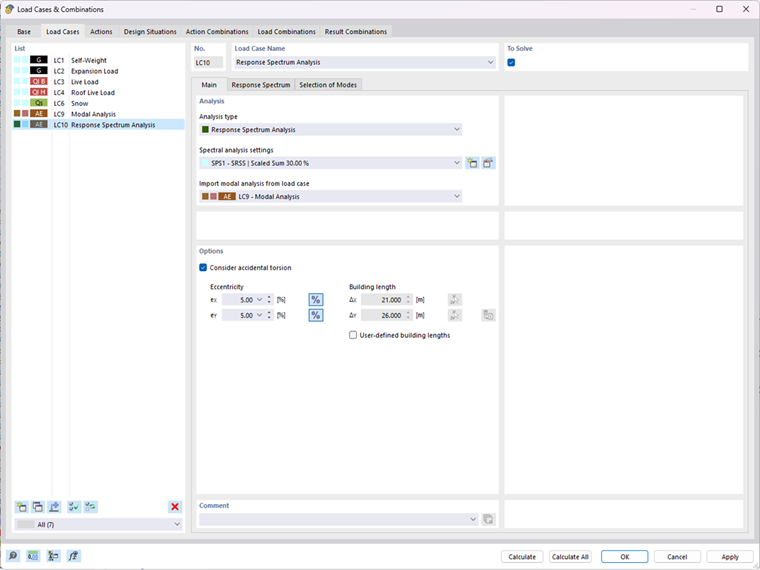
Un calcul selon l’analyse du spectre de réponse est ensuite requis.

Création d’une analyse du spectre de réponse

Si l’entrée est complète, vous pouvez analyser les résultats après le calcul. Les propriétés importantes pour l’analyse dynamique sont disponibles dans le tableau des résultats de l’analyse spectrale. La sous-catégorie Résultats par étage contient également le coefficient de sensibilité de chaque étage.

Affichage des résultats des étages et du coefficient de sensibilité

Après avoir calculé le coefficient de sensibilité du déplacement entre les étages, une distinction des cas concernant la pertinence de l’analyse du second ordre est effectuée selon l’EN 1998-1, 2.2.2 et 4.4.2.2 [1] :

Distinction des cas pour l’analyse du second ordre

1. Coefficient de sensibilité θ ≤ 0,1

L’analyse du second ordre ne doit pas être considérée.

2. Coefficient de sensibilité 0,1 < θ ≤ 0,2

L’analyse du second ordre peut être considérée approximativement par un facteur égal à 1/(1−θ).

3. Coefficient de sensibilité 0,2 < θ ≤ 0,3

L’analyse du second ordre doit être considérée directement. Cette opération peut être effectuée en ajustant la matrice de rigidité géométrique dans RFEM 6 et RSTAB 9. En savoir plus : ko | Considération de la théorie du second ordre dans une analyse dynamique dans RFEM 6 et RSTAB 9

4. Coefficient de sensibilité 0,3 < θ

Le concept de la structure n’est pas valide et doit être modifié.

Auteur

M. Eichner est responsable du développement de produits pour les analyses dynamiques et fournit une assistance technique à nos clients.

Liens

Références

l'EN 1998-1. (2013). Eurocode 8 : Calcul des structures pour leur résistance aux séismes - Partie 1 : Règles générales, Actions sismiques et règles pour les bâtiments, EN 1998-1:2004/A1:2013.
Eurocode 0 : Base du calcul de structure, EN 1990:2010-12.
Werle, H. Finite Elemente in der Baustatik, 3. édition. Wiesbaden : Vieweg & Sohn, 2008

;