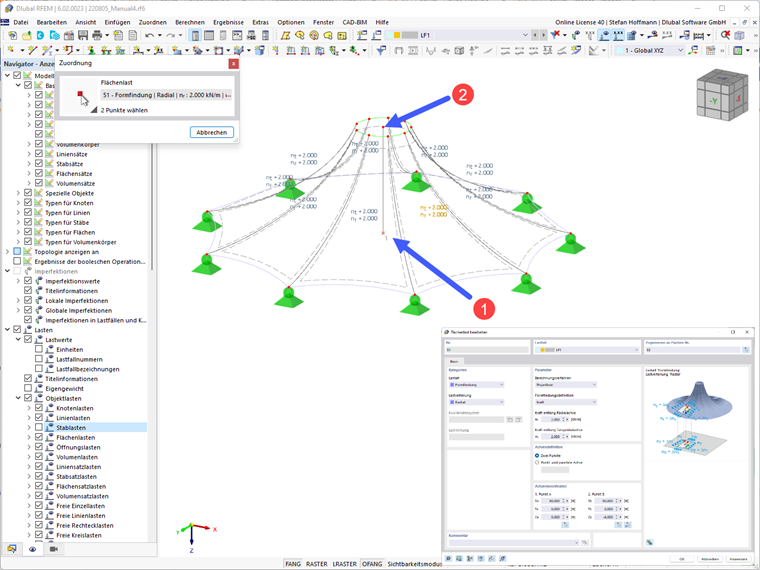
Definicja obciążeń formujących odbywa się poprzez odpowiednie obciążenia obiektów. Można zdefiniować obciążenia powierzchniowe, prętowe i objętościowe.
Obciążenia powierzchniowe i prętowe mają typ obciążenia formowanie. Dla obciążeń objętościowych wybiera się typ obciążenia gaz.
Dla w modelu podzielonych, ale faktycznie powiązanych obiektów istnieją także obciążenia zestawów prętów, zestawów powierzchni oraz zestawów objętości. Koncepcja tych obciążeń odpowiada tym obciążeniom regularnym, więc nie są one ponownie explicite wymieniane.
Obciążenia prętowe
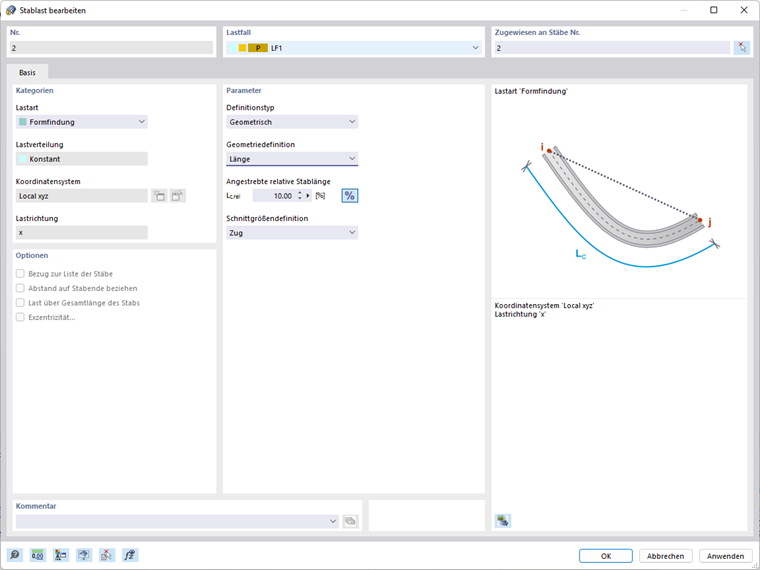
Obciążenia prętowe typu obciążenia formowanie mogą być definiowane geometrycznie lub jako siła.
Obciążenia prętowe - geometryczny typ definicji
Geometryczny typ definicji pozwala na definiowanie formy za pomocą następujących możliwości:
- Długość (Lc)
- Niezatłoczona długość (Lmfg)
- Ugięcie (S)
- Maksymalne pionowe ugięcie (Smax | Kierunek obciążenia ZL)
- Minimalne ugięcie dolnego punktu (Slow | Kierunek obciążenia ZL)
We wszystkich geometrycznych obciążeniach można je ustalić relatywnie lub absolutnie. Zmiana pomiędzy absolutną a relatywną definicją może być dokonana poprzez kliknięcie na symbol
. Nazwa obciążenia zawiera przy relatywnej definicji skrót rel.
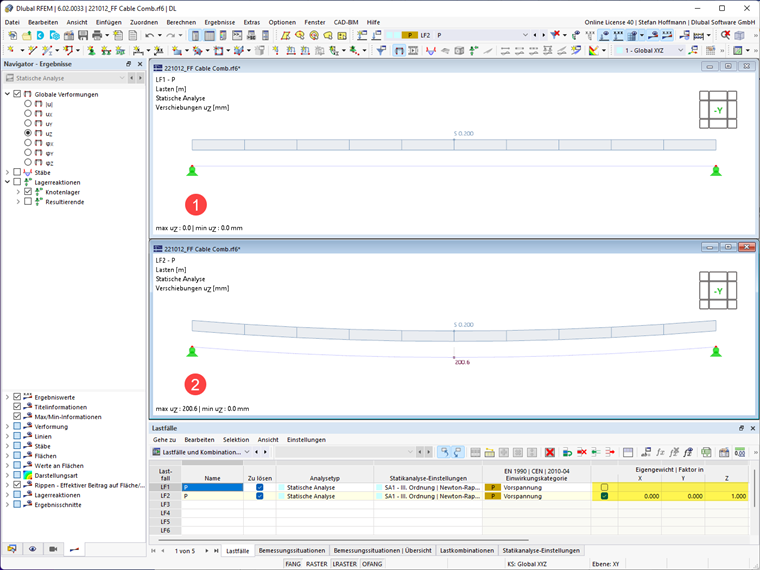
Dla wszystkich geometrycznych obciążeń możliwa jest definicja wartości sił wewnętrznych na rozciąganie lub ściskanie. Ważne jest, aby zauważyć, że liny z definicji mogą przyjmować tylko siły rozciągające. Pręt natomiast może przyjmować formę pod wpływem rozciągania lub ściskania.
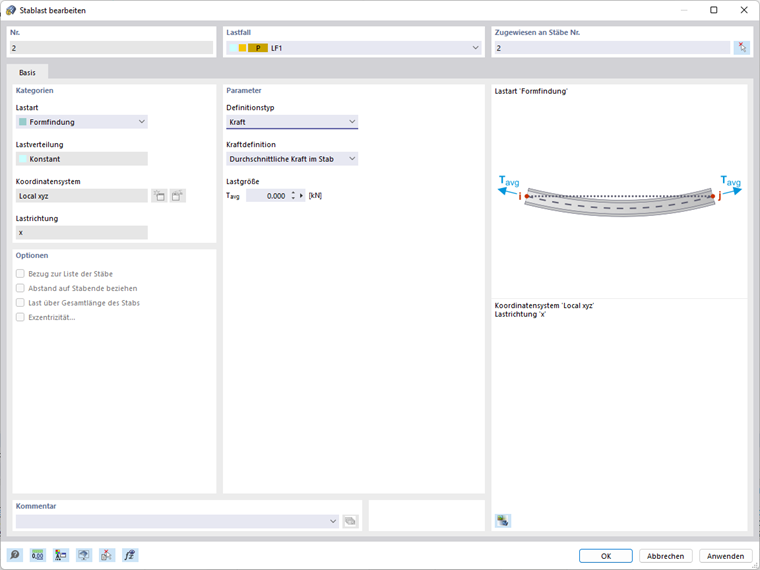
Obciążenia prętowe - typ definicji siła
Typ definicji siła pozwala na definiowanie formy za pomocą następujących możliwości:
- Średnia siła w pręcie (Tavg)
- Maksymalna siła w pręcie (Tmax)
- Minimalna siła w pręcie (Tmin)
- Składowa pozioma siły rozciągającej (Fx)
- Siła rozciągająca na końcu i (Ti | Początek pręta)
- Siła rozciągająca na końcu j (Tj | Koniec pręta)
- Minimalna siła rozciągająca na końcu i (Tmin, i | Początek pręta)
- Minimalna siła rozciągająca na końcu j (Tmin, j | Koniec pręta)
- Gęstość siły (FD)
Obciążenia powierzchniowe
Obciążenia powierzchniowe mogą mieć definicję formowania jako siła lub naprężenie. Można wybierać pomiędzy metodą standardową a metodą rzutowania . Dodatkowo, w metodzie standardowej dostępna jest definicja formowania poprzez ugięcie.
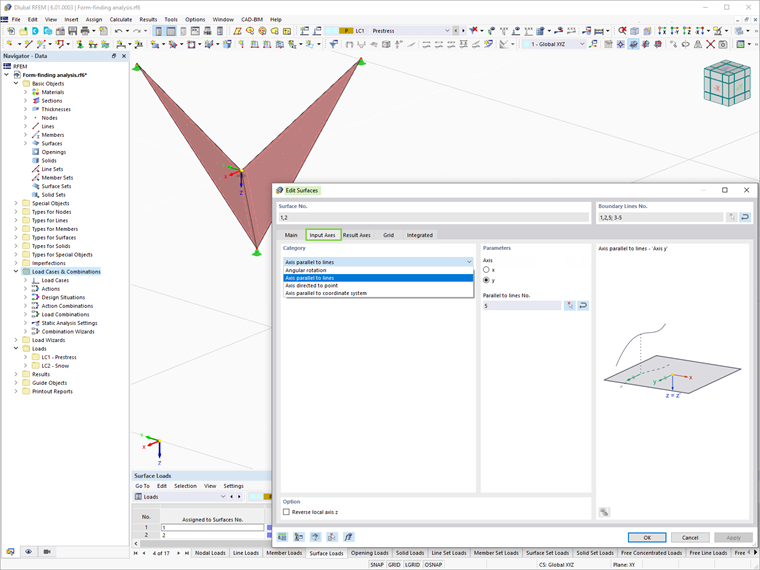
Ważne jest wspomnienie, że dla założenia ortotropowego naprężenia powierzchniowego należy zaznaczyć opcję osi specyficznych w dialogu edytowania powierzchni i odpowiednio dostosować parametry wejściowe powierzchni.
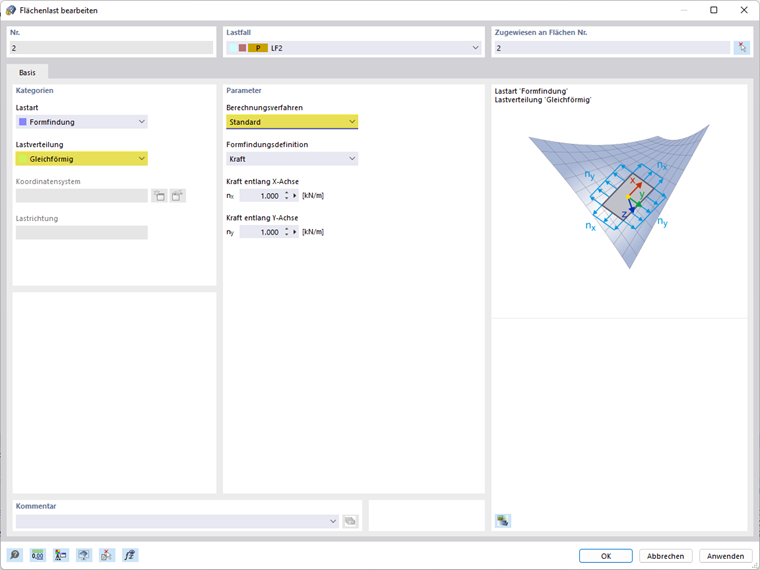
Obciążenie powierzchniowe - metoda standardowa
Metoda standardowa opisuje wektor, który może swobodnie poruszać się w przestrzeni do pozycji docelowej.
Obciążenie powierzchniowe - ugięcie metoda standardowa
Definiując ugięcie, można z góry określić wychylenie membrany, umożliwiając modelowanie, zwłaszcza poduszek. Określasz, jak daleko powierzchnia może się wychylić, a odpowiednia definicja siły jest automatycznie ustalana iteracyjnie. Trzeba tylko zdefiniować proporcje sił w nx i ny.
Ugięcie może być odniesione do następujących wyimaginowanych płaszczyzn:
- Podstawa
- Układ współrzędnych
- Powierzchnia
Podstawa odnosi się do samej powierzchni. Wykorzystuje się płaszczyznę bazową. W przypadku zakrzywionej powierzchni są to zwykle podparte krawędzie.
Układ współrzędnych odnosi się do zdefiniowanego układu współrzędnych. Ważna jest tu oś Z (przy obróconym układzie współrzędnych oś W). Ugięcie mierzy się jako odległość od powierzchni do osi.
Ugięcie można także zdefiniować w odniesieniu do innej powierzchni.
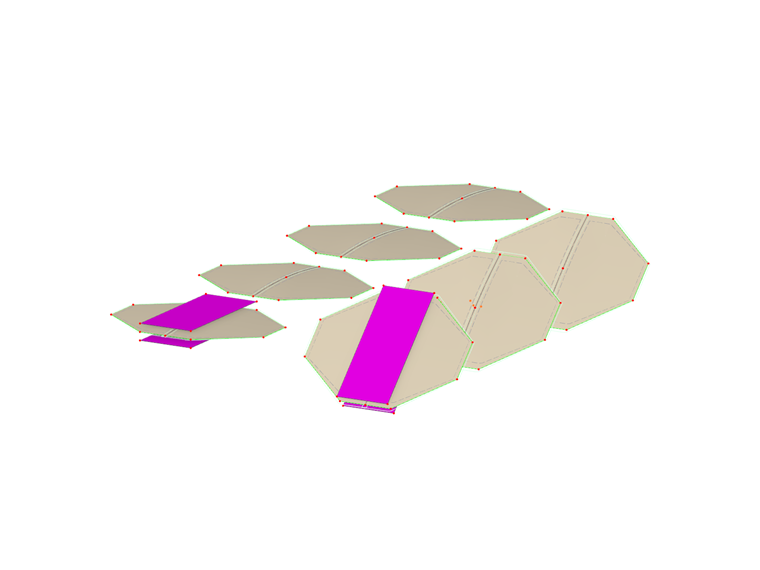
W poniższym modelu przedstawiono różne modelowania.
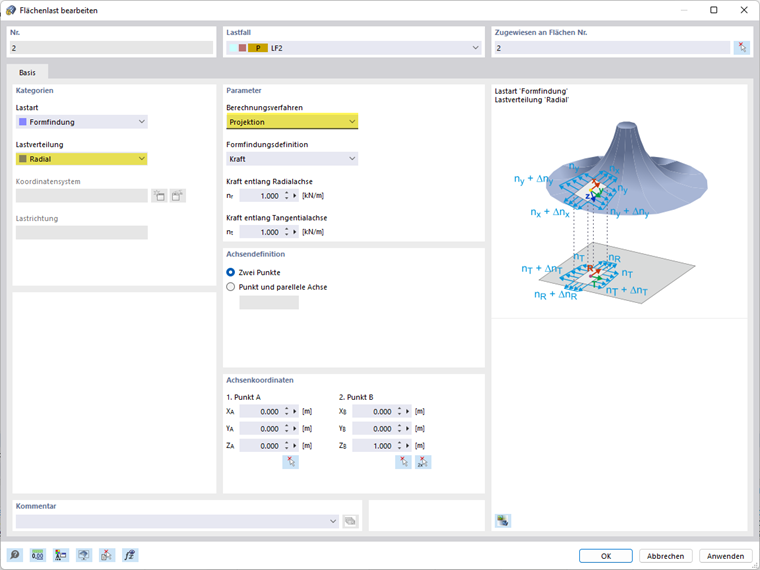
Obciążenie powierzchniowe - metoda rzutowania
Metoda rzutowania może być w RFEM 6 definiowana ortogonalnie lub promieniście.
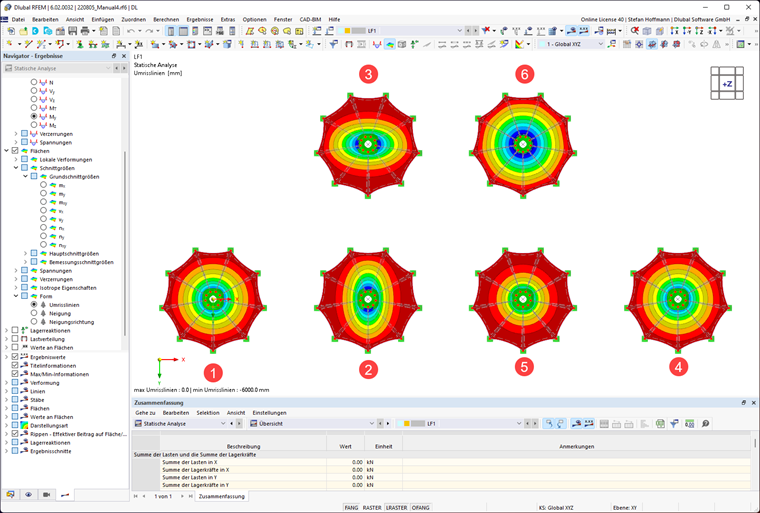
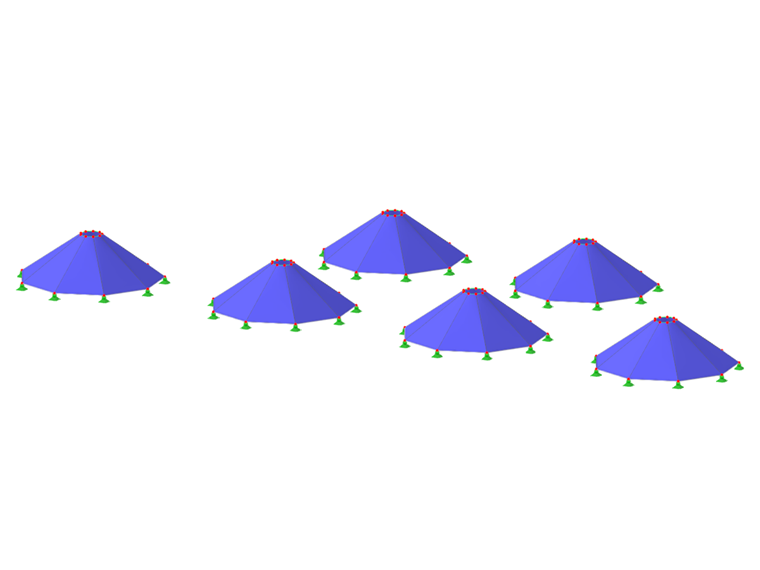
Dla porównania metody rzutowania ortogonalnego i promienistego poniżej znajduje się plik modelu.
Obciążenia powierzchniowe są zdefiniowane w następujący sposób:
| Numer | Rozkład obciążenia | Definicja siły [kN/m] | Definicja siły [kN/m] | Forma | Przyczyna |
|---|---|---|---|---|---|
| 1 | Ortogonalny | nx = 2 | ny = 2 | kołowy | jednakowe naprężenie w X i Y |
| 2 | Ortogonalny | nx = 2 | ny = 10 | eliptyczny | wyższe naprężenie w Y |
| 3 | Ortogonalny | nx = 10 | ny = 2 | eliptyczny | wyższe naprężenie w X |
| 4 | Promienisty | nr = 2 | nt = 2 | kołowy | jednakowe naprężenie w r i t |
| 5 | Promienisty | nr = 2 | nt = 10 | kołowy, stromy stożek | wyższe naprężenie w t |
| 6 | Promienisty | nr = 10 | nt = 2 | kołowy, płaski stożek | wyższe naprężenie w r |
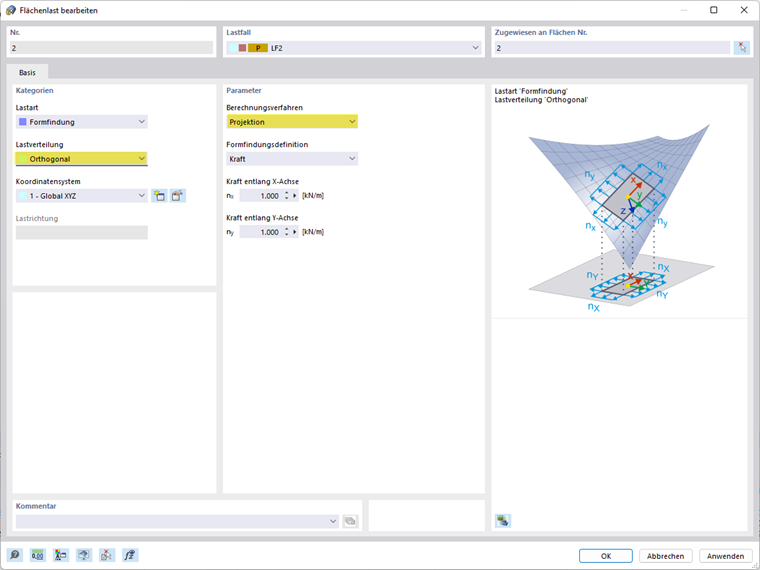
Obciążenie powierzchniowe - ortogonalna metoda rzutowania
Ortogonalna metoda rzutowania opisuje wektor zamocowany częściowo w przestrzeni i ustalony na globalnych współrzędnych XY.
Obciążenie powierzchniowe - promienista metoda rzutowania
Promienista metoda rzutowania opisuje wektor zamocowany częściowo w przestrzeni i ustalony na zdefiniowanych osiach promienistych i stycznych.
Dla promienistej metody rzutowania trzeba zdefiniować oś. Możesz łatwo złapać 2 punkty w swoim modelu za pomocą przycisku
. Zazwyczaj jest to pionowa oś w centrum twojej membrany stożkowej.
Obciążenia objętościowe
Obciążenia objętościowe typu obciążenia gaz mogą być definiowane na podstawie różnych zachowań gazu.
Obciążenia objętościowe - typ obciążenia gaz
Typ obciążenia gaz umożliwia definiowanie formy na podstawie następujących zachowań gazu:
- Wynikowe nadciśnienie (po)
- Wzrost nadciśnienia (Δpo)
- Wynikowa objętość (V)
- Wzrost objętości (ΔV)
Oznaczenia są zdefiniowane następująco:
| Skrót | Oznaczenie |
|---|---|
| p | Ciśnienie gazu |
| pp | Początkowe ciśnienie gazu (ciśnienie atmosferyczne) |
| po | Nadciśnienie gazu |
| Δpo | Wzrost nadciśnienia gazu |
| pa | Aktualne ciśnienie gazu (odpowiada pp bez stanu początkowego/budowlanego) |
| V | Objętość gazu |
| Va | Aktualna objętość gazu |
| ΔV | Wzrost objętości |
| T | Temperatura gazu |
| Tp | Początkowa temperatura gazu |
