Zatížení při form-findingu

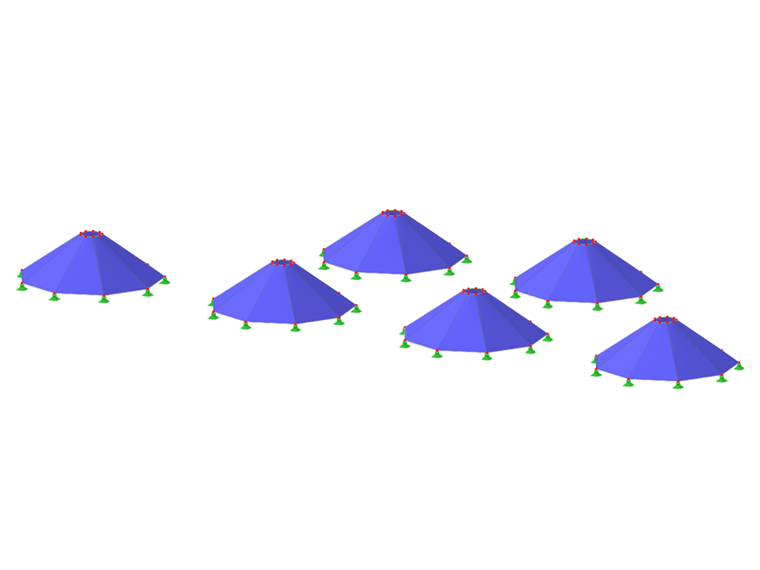
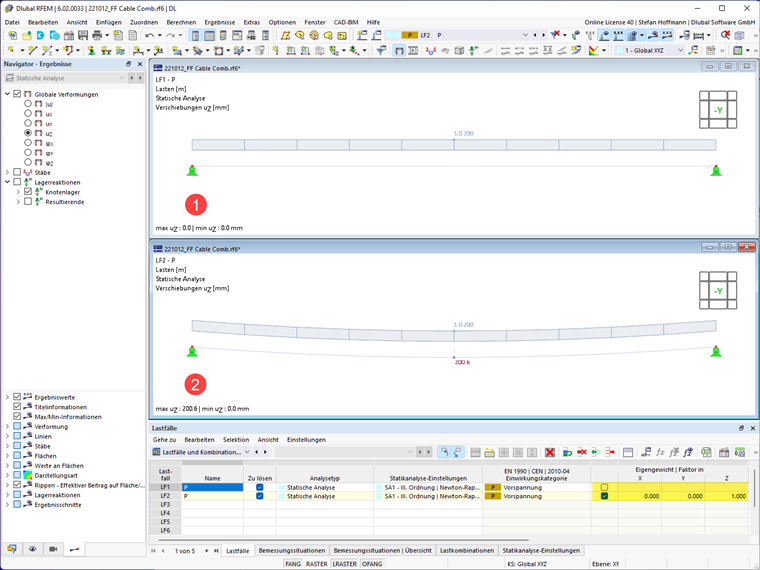
Definice zatížení pro form-finding se určuje prostřednictvím příslušných zatížení objektů. Můžete definovat zatížení na plochu, zatížení prutů a zatížení objemu.

Zatížení ploch a prutů jsou druhu zatížení form-finding. Pro objemové zatížení zvolte druh zatížení plyn.

Pro objekty rozdělené v modelu, ale v podstatě související, existují také zatížení sady prutů, zatížení sady ploch i zatížení sady objemů. Koncept těchto zatížení odpovídá pravidelným zatížením, takže je není nutné výslovně uvádět.

Zatížení prutů

Zatížení prutů druhu zatížení form-finding mohou být definována geometricky nebo jako síla.

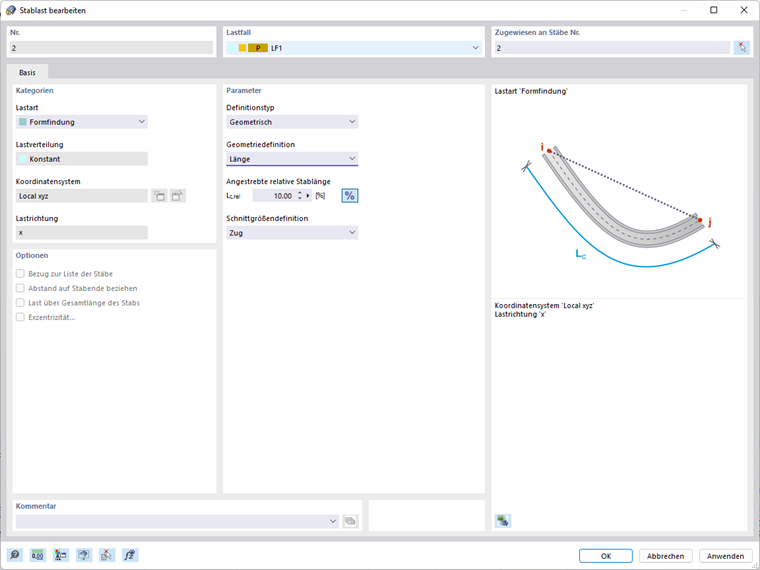
Zatížení prutů - Typ definice geometricky

Zatížení na prut, Hledání tvaru, geometrie

Typ definice Geometricky umožňuje definovat formu pomocí následujících možností:

• Délka (L_c)
• Nezatížená délka (L_mfg)
• Prověšení (S)
• Maximální vertikální prověšení (S_max | směr zatížení Z_L)
• Vertikální prověšení na nízkém bodu (S_low | směr zatížení Z_L)

U všech geometrických zatížení máte možnost je stanovit relativně nebo absolutně. Změna mezi absolutní a relativní definicí může být provedena kliknutím na symbol . Označení zatížení zahrnuje v případě relativní definice zkratku rel.

Pro všechna geometrická zatížení může být definována vnitřní síla jako tah nebo tlak. Je důležité si uvědomit, že lana mohou přijímat pouze tah díky svému definování. Na druhé straně u nosníku může být nalezena forma tahového nebo tlakového zatížení.

• 3D prohlížeč
• 3D prohlížeč | Babylon
• Virtuální realita

Hledání tvaru bez a s vlastní tíhou

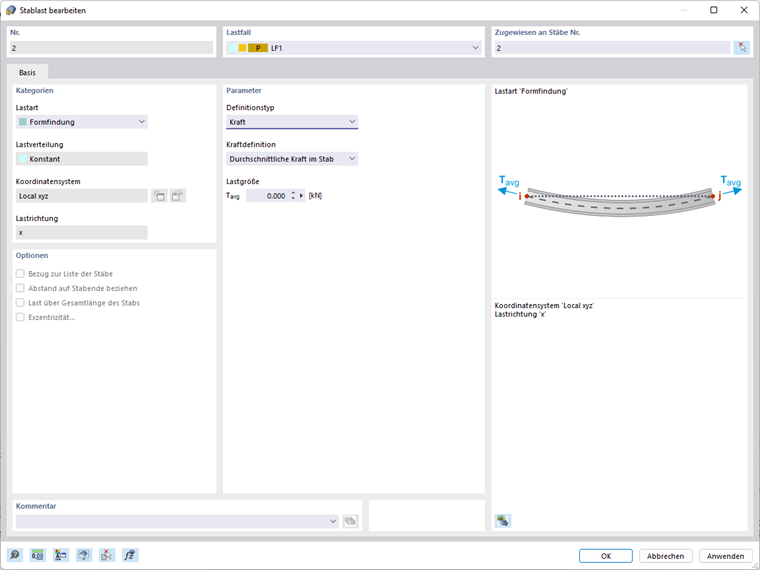
Zatížení prutů - Typ definice síla

Zatížení na prut, síla

Typ definice Síla umožňuje definovat formu pomocí následujících možností:

• Průměrná síla v prutu (T_avg)
• Maximální síla v prutu (T_max)
• Minimální síla v prutu (T_min)
• Horizontální tahová složka (F_x)
• Tah na konci i (T_i | Počátek prutu)
• Tah na konci j (T_j | Konec prutu)
• Minimální tah na konci i (T_{min, i} | Počátek prutu)
• Minimální tah na konci j (T_{min, j} | Konec prutu)
• Hustota síly (FD)

Zatížení ploch

Zatížení ploch mohou mít definici form-findingu jako Sílu nebo Napětí. Můžete si vybrat mezi standardní metodou a projekční metodou . Navíc je v rámci standardní metody k dispozici definice form-findingu jako Prověšení.

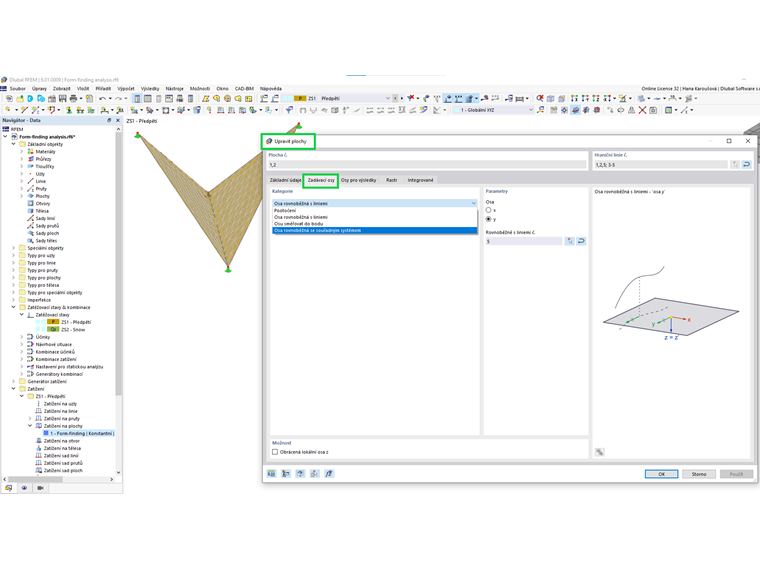
Je důležité zmínit, že pro použití ortotropní povrchové předpětí by mělo být v dialogu "Upravit plochy" zaškrtnuto políčko specifické osy a vstupní parametry ploch by měly být přizpůsobeny.

• 3D prohlížeč
• 3D prohlížeč | Babylon
• Virtuální realita

Vstupní osy membrány

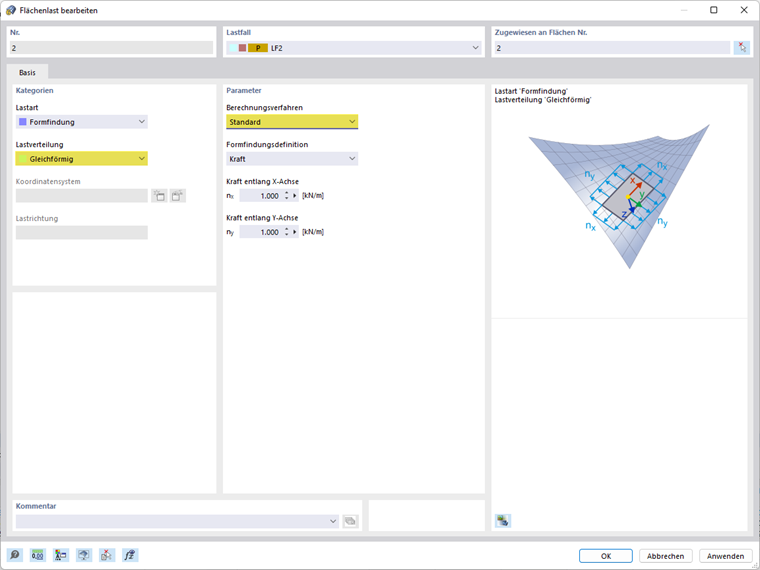
Zatížení ploch - Standardní metoda

Standardní metoda popisuje vektor, který se může volně pohybovat v prostoru až do cílové polohy.

Form-finding zatížení plochy, standardní metoda

Zatížení ploch - Prověšení Standardní metoda

S definicí prověšení máte možnost určit vychýlení membrány a tím především modelovat polštáře. Určíte, jak daleko může být plocha vychýlena, přičemž příslušná definice síly bude automaticky a iterativně zjištěna. Musíte pouze definovat poměr sil v n_x a n_y.

Prověšení může být stanoveno na následující imaginární roviny:

• Základna
• Souřadnicový systém
• Plocha

Základna odkazuje na samotnou plochu. Používá se základní rovina. U zakřivené plochy jsou to zpravidla podepřené okraje.

Souřadnicový systém odkazuje na definovaný souřadnicový systém. Zde je směrodatná osa Z (u otočeného souřadnicového systému osa W). Prověšení se měří jako vzdálenost od plochy k ose.

Prověšení může být také definováno ve vztahu k jiné ploše.

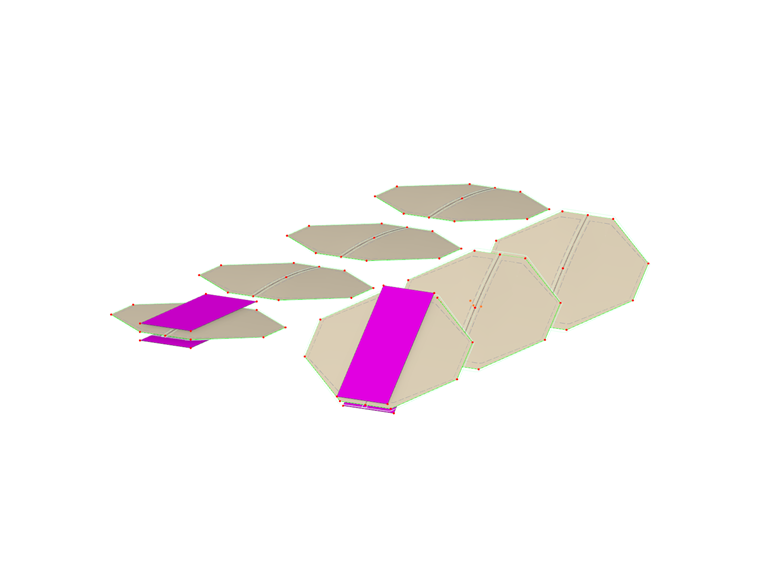
V následujícím modelu jsou uvedeny různé modelace.

• 3D prohlížeč
• 3D prohlížeč | Babylon
• Virtuální realita

Fóliový polštář - průvěs

Zatížení ploch - Projekční metoda

Projekční metoda může být v RFEM 6 definována ortogonálně nebo radiálně.

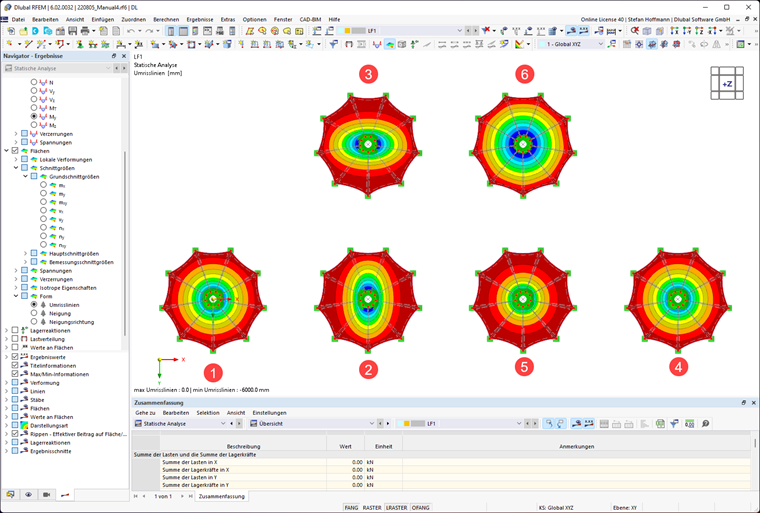
Pro porovnání ortogonální a radiální projekční metody následuje soubor modelu.

• 3D prohlížeč
• 3D prohlížeč | Babylon
• Virtuální realita

Kuželová membrána - obrysové linie

Zatížení ploch jsou definována takto:

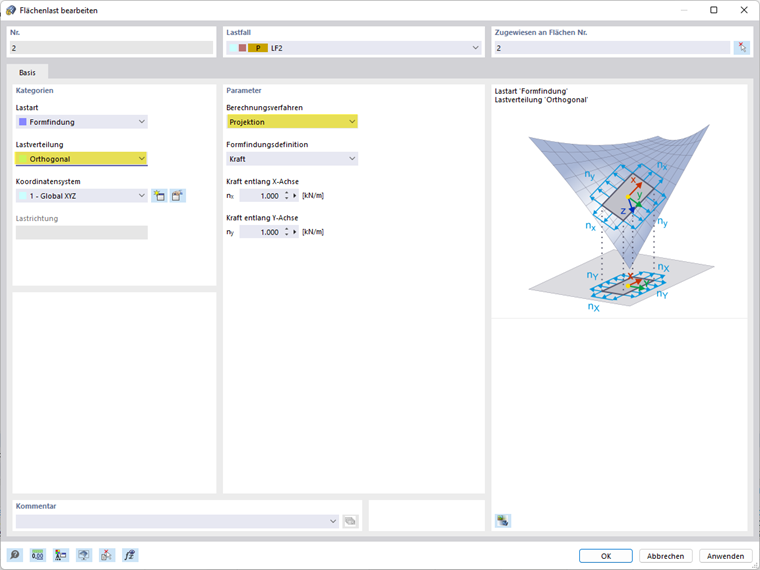
Zatížení ploch - Ortogonální projekční metoda

Ortogonální projekční metoda popisuje vektor částečně pohyblivý v prostoru a fixovaný na globálními XY souřadnicemi.

Hledání tvaru zatížení plochy, metoda projekce - ortogonální

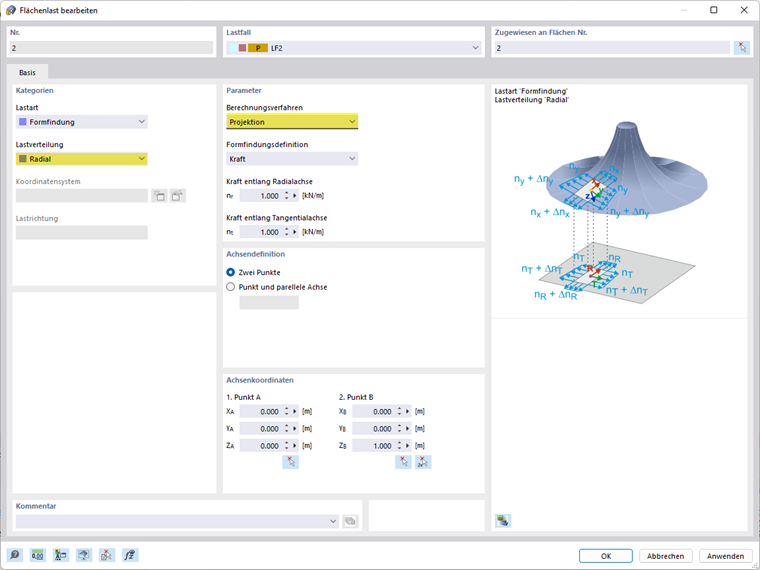
Zatížení ploch - Radiální projekční metoda

Radiální projekční metoda popisuje vektor částečně pohyblivý v prostoru a fixovaný na definovaných radiálních a tangenciálních osách.

Hledání tvaru zatížení plochy, projekční metoda - radiální

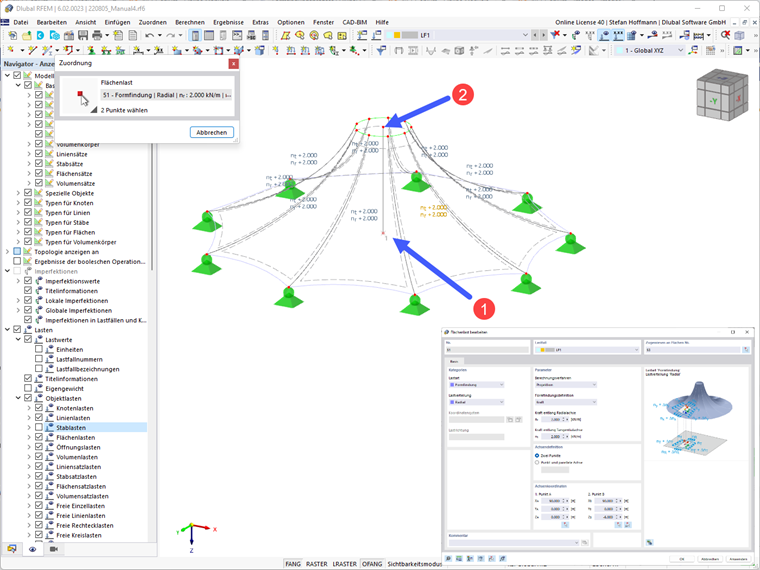
Pro radiální projekční metodu musíte definovat osu. Můžete k tomu snadno chytit 2 body ve vašem modelu pomocí tlačítka . Obvykle se jedná o svislou osu uprostřed vaší kuželové membrány.

• 3D prohlížeč
• 3D prohlížeč | Babylon
• Virtuální realita

Kuželová membrána - metoda radiální projekce

Zatížení objemu

Objemová zatížení druhu plyn mohou být definována na základě různých chování plynů.

Objemové zatížení: Typ zatížení Plyn

Zatížení objemu - Druh zatížení plyn

Druh zatížení plyn umožňuje definovat formu na základě následujících chování plynů:

• Výsledný přetlak (p_o)
• Zvýšení přetlaku (Δ_po)
• Výsledný objem (V)
• Zvýšení objemu (Δ_V)

Označení jsou definována takto: