2018 Wymiarowanie słupów drewnianych NDS w RFEM 6

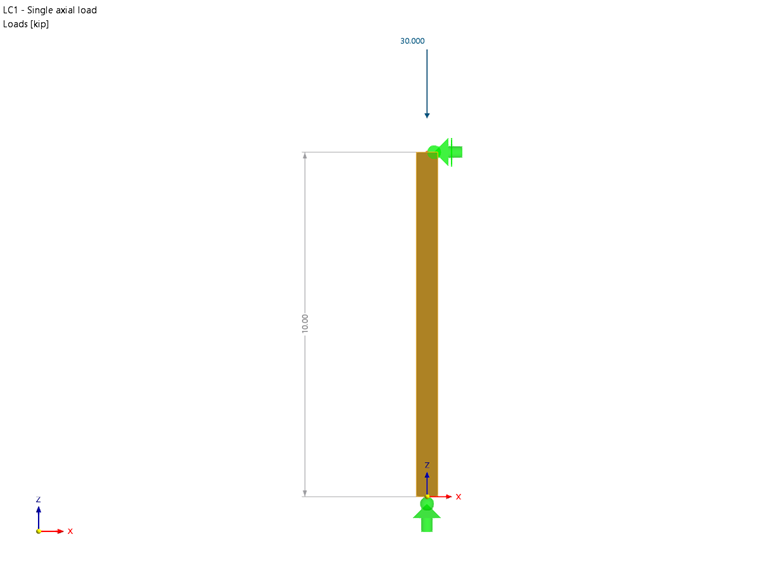
Zaprojektowany zostanie słup o konstrukcji Alaska Cedar Select o długości 3 m i nominalnie 8 cali ⋅ 8 cali, o obciążeniu osiowym 30,00 kips. Celem analizy jest wyznaczenie współczynników dostosowawczych z uwagi na ściskanie oraz skorygowanej wartości obliczeniowej nośności na ściskanie słupa. A normal load duration and pinned supports at each end of the member are assumed. The loading criteria are simplified for this example. Normal loading criteria can be referenced in Sec. 1.4.4 [1]. In Image 01 and 02 is a diagram of the simple column and section properties respectfully.

• 3D Viewer | Google
• 3D Viewer | Babylon
• Wirtualna rzeczywistość

1 Model słupa drewnianego

2 Właściwości przekrojów

Column Properties

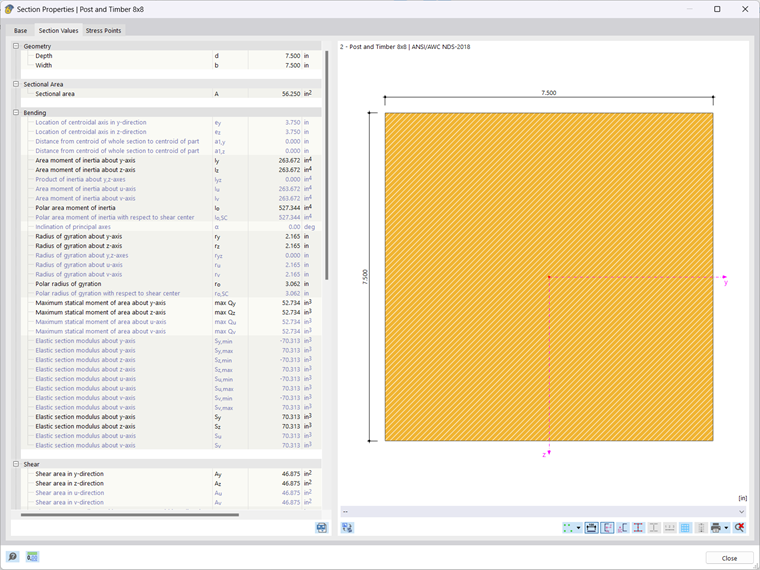
The cross-section used in this example is an 8 inch square post. The cross-section properties of the timber column are shown below:

b = 7.50 in, d = 7.50 in, L = 10.00 ft

Powierzchnia przekroju brutto:

A_g = b ⋅ d = 7.50 in ⋅ 7.50 in = 56.25 in²

Moment statyczny przekroju:

Moment bezwładności przekroju:

The material used is "Alaska Cedar, 5"x5" and Larger, Beam and Stringer, Select Structural". Właściwości materiału są następujące:

Referencyjna wytrzymałość obliczeniowa na ściskanie:

F_c = 925 psi

Minimalny moduł sprężystości:

E_min = 440 ksi

Współczynniki korekcyjne dla słupów

For the design per the 2018 NDS standard and the ASD method, stability factors (or adjustment factors) must be applied to the compressive design value (f_c). To z kolei pozwala uzyskać skorygowaną wartość obliczeniowej wytrzymałości na ściskanie (F '_c). The factor F'_c is calculated with the following equation, highly dependent on the listed adjustment factors from Table 4.3.1 [1]:

F'_c = F_c ⋅ C_D ⋅ C_M ⋅ C_t ⋅ C_f ⋅ C_i ⋅ C_P

Poniżej określany jest każdy z poszczególnych współczynników korekcyjnych:

C_D – The load duration factor is implemented to take into account different periods of loading. C_D uwzględniane jest w przypadku obciążenia śniegiem, wiatrem i trzęsieniem ziemi. This factor must be multiplied by all reference design values except for the modulus of elasticity (E), modulus of elasticity for beam and column stability (E_min), and the compression forces perpendicular to the grain (F_c) based on Sec. 4.3.2 [1]. C_D in this case is set to 1.00 as per Sec. 2.3.2 [1] assuming a load duration of 10 years.

C_M – The wet service factor references design values for structural sawn lumber based on moisture service conditions specified in Sec. 4.1.4 [1]. In this case, based on Sec. 4.3.3 [1], C_M is set to 0.910.

C_t – The temperature factor is controlled by a member's sustained exposure to elevated temperatures up to 150 degrees Fahrenheit. Wszystkie wartości referencyjne obliczeniowe są mnożone przez Ct. Utilizing Table 2.3.3 [1], C_t is set to 1.00 for all reference design values, assuming temperatures are equal to or lesser than 100 degrees Fahrenheit.

C_F – The size factor for sawn lumber does not consider wood as a homogeneous material. The size of the column and type of wood are taken into account. For this example, our column has a depth lesser than or equal to 12 inches. Referencing Table 4D based on the size of the column, a factor of 1.00 is applied. This info can be found in Sec. 4.3.6.2 [1].

C_i – The incising factor considers the preservation treatment applied to the wood to resist decay and avoid fungal growth. Most of the time this involves pressure treatment, but in some cases requires the wood to be incised increasing the surface area for chemical coverage. W tym przykładzie zakłada się, że drewno jest perforowane (nacinane). Referencing Table 4.3.8 [1], an overview of the factors by which each member property must be multiplied is shown.

Skorygowany moduł sprężystości

Należy również zmodyfikować referencyjny moduł sprężystości (E i E_min). The adjusted modulus of elasticity (E' and E'_min) are determined from Table 4.3.1 [1] and the incising factor C_i is equal to 0.95 from Table 4.3.8 [1].

E' = E ⋅ C_M ⋅ C_t ⋅ C_i = 1,140,000.00 psi

E'_min = E_min ⋅ C_M ⋅ C_t ⋅ C_i = 418,000.00 psi

Współczynnik stateczności dla słupa (C_P)
Współczynnik stateczności dla słupa (C_P) jest wymagany do obliczenia skorygowanej wartości obliczeniowej nośności na ściskanie słupa i stopnia wykorzystania. Poniższe kroki zawierają wzory i współczynniki niezbędne do znalezienia C_P.

The equation used to calculate C_P is Eqn. (3.7-1) referenced in Section 3.7.1.5. Poniżej obliczana jest skorygowana obliczeniowa wytrzymałość na ściskanie równolegle do włókien (F_c):

F'_c = F_c ⋅ C_D ⋅ C_M ⋅ C_t ⋅ C_F ⋅ C_i = 673.40 psi

Kolejna wartość wyliczana wzorem (3.7-1) to krytyczna wartość obliczeniowa dla wyboczenia prętów ściskanych (F_cE ).

Współczynnik smukłości oblicza się następująco:

Współczynnik smukłości podstawia się do równania na F_cE i obliczana jest następująca wartość:

F_cE = 1342.17 psi

The last variable needed is (c), which is equal to 0.8 for sawn lumber. Wszystkie zmienne mogą zostać podstawione do równania (3.7-1) by uzyskać wartość C_P.

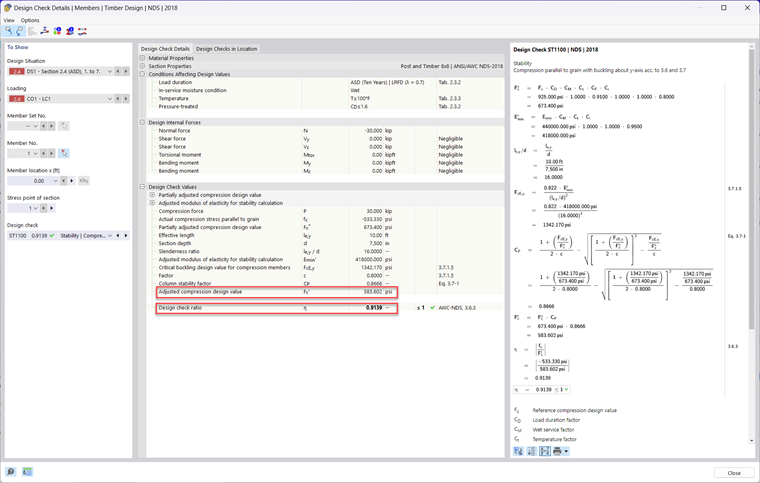
Now, all adjustment factors have been determined from Table 4.3.1 [1]. Therefore, the adjusted compressive design value parallel to grain (F'_c) can be calculated.

F'_c = F_c ⋅ C_D ⋅ C_M ⋅ C_t ⋅ C_F ⋅ C_i ⋅ C_P = 583.602 psi

Kryterium obliczeniowe dla słupa

Głównym celem tego przykładu jest określenie stopnia wykorzystania dla słupa. W ten sposób można zweryfikować czy rozmiar przekroju pręta jest odpowiedni dla określonego obciążenia lub czy możliwa jest dalsza optymalizacja. Calculating the design ratio requires the adjusted compressive design value parallel to the grain about both axes (F'_c) and actual compressive stress parallel to the grain (f_c). In this case, the cross-section is symmetrical, so F'_c is equivalent for both the x- and the y-axis.

Rzeczywiste naprężenie ściskające (f_c) oblicza się w następujący sposób:

The adjusted compressive design value parallel to the grain (F'_c) and the actual compressive stress (f_c) are used to compile the design ratio (η) as per Sec. 3.6.3.

RFEM 6 Verification

When designing timber per the 2018 NDS standard in RFEM 6, the Timber Design Add-on analyzes and optimizes cross-sections based on loading criteria and member capacity for a single member or a set of members. Są one dostępne dla obu metod obliczeniowych: LRFD oraz ASD. The results between the analytical example and RFEM 6 are compared and verified below.

Editing the Member is where the Design Properties like the Effective Lengths, Service Conditions, Design Configurations and Design Supports can be adjusted for design. The material and cross-section are defined here as well. The moisture service condition is set to Wet and the temperature is equal to or less than 100 degrees Fahrenheit. Lateral-Torsional Buckling is defined according to Table 3.3.3 [1]. The material is set to "User-Defined" and considered "Incised".

Adjusted Compression Design Value Parallel to Grain:

F'_c = 1.000

Design Ratio:

η = 1.000

3 RFEM 6 – Wyniki wymiarowania drewna