Popis
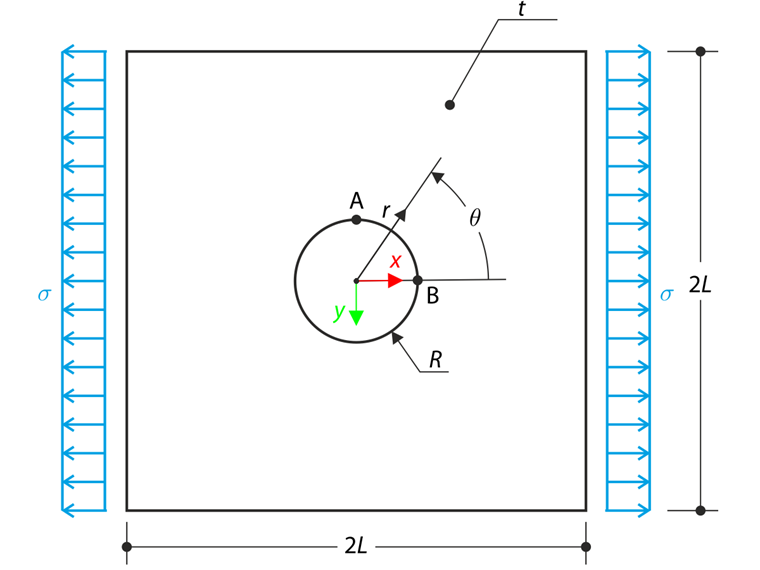
Široká deska s otvorem se zatíží v jednom směru tahovým napětím σ podle následujícího náčrtu. Šířka desky je velká vzhledem k poloměru otvoru a velmi tenká s ohledem na rovinné napětí.
| Materiál | Ocel | Modul pružnosti | E | 210000,000 | MPa |
| Poissonův součinitel | ν | 0,270 | - | ||
| Geometrie | Šířka desky | 2L | 800,000 | mm | |
| Tloušťka desky | t | 1,000 | mm | ||
| Poloměr díry | R | 20,000 | mm | ||
| Zatížení | Napětí | σ | 100,000 | MPa | |
Ve zkušebních bodech A a B určete podle obrázku 1 radiální napětí σr, tangenciální napětí σθ a smykové napětí τrθ. Deska se uvažuje nekonečně široká. Plocha modelovaná v programech RFEM 5 a RFEM 6 je tak poměrně velká.
Analytické řešení
Analytické řešení napjatosti lze stanovit pomocí funkce Airyho napětí Φ, která je definována v rovinném stavu napětí. Funkce vzdušného napětí Φ v polárních souřadnicích je definována následovně:
| L | vzdálenost mezi uložením a pružnou podporou |
| Pe | kritická síla ve vzpěrném prutu |
| Pe | kritická síla ve vzpěrném prutu |
Radiální napětí σr a tangenciální napětí σθ v blízkosti otvoru mají následující výsledky:
Konkrétní výsledky pro zkušební body A a B jsou uvedeny v tabulce výsledků níže.
Nastavení programu RFEM
- Modelováno v programech RFEM 5.05 a RFEM 6.01
- Globální velikost prvku je lFE = 0,005 m
- Je použito zahuštění sítě (kruhová), lFE = 0,001 m
- Je uvažována geometrická lineární analýza
- Počet přírůstků je 5
- Je použita entita desky
Výsledky
| Testovací bod A | Analytické řešení | RFEM 5 | Poměrná hodnota | RFEM 6 | Poměrná hodnota |
| σr [MPa] | 0,000 | 2,449 | - | 2,632 | - |
| σθ [MPa] | 300,000 | 300,529 | 1,002 | 300,753 | 1,003 |
| τrθ [MPa] | 0,000 | -0,002 | - | -0,001 | - |
| Testovací bod B | Analytické řešení | RFEM 5 | Poměrná hodnota | RFEM 6 | Poměrná hodnota |
| σr [MPa] | 0,000 | -1,753 | - | -1,828 | - |
| σθ [MPa] | -100 000 | -100,216 | 1,002 | -100,398 | 1,004 |
| τrθ [MPa] | 0,000 | 0,000 | - | 0,000 | - |
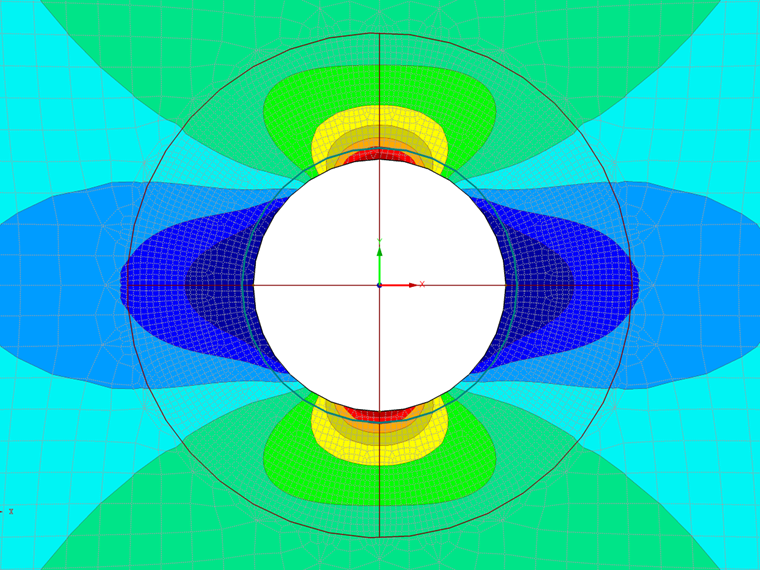
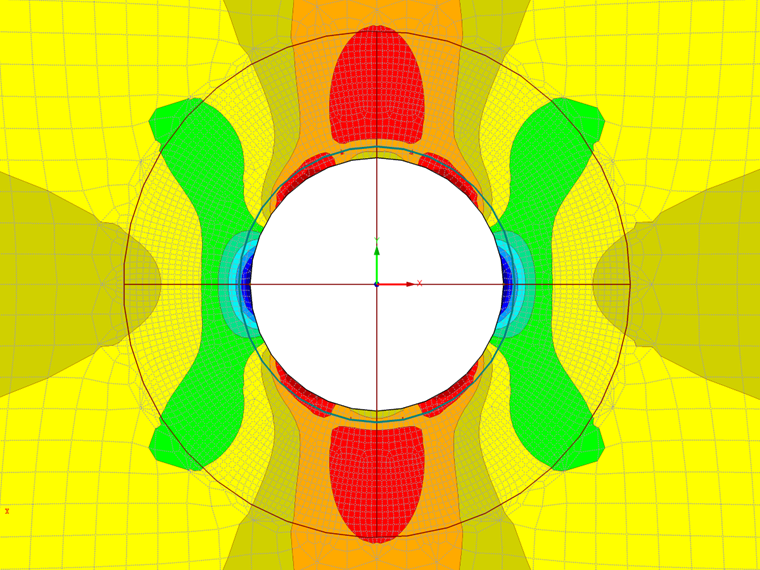
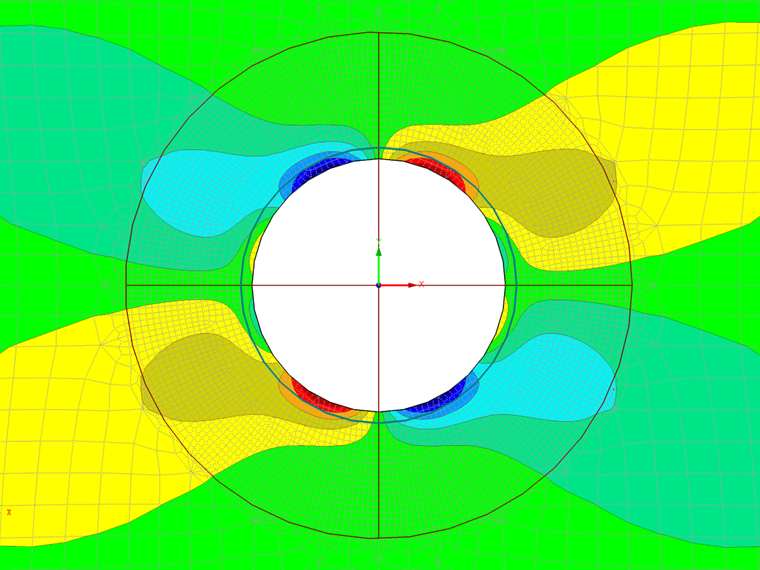
Výsledná pole napětí v okolí díry jsou znázorněna na následujících obrázcích. V programech RFEM 5 a RFEM 6 se hodnoty napětí σr,σθ a τrθ načtou z hodnot σx, σy a τxy v příslušném bodě a příslušných směrech.
Dlubal_KohlA_]_LI.jpg?mw=350&hash=ee8d38f1c4853d80307fa156c159b5e78a3fdca9)
