Description
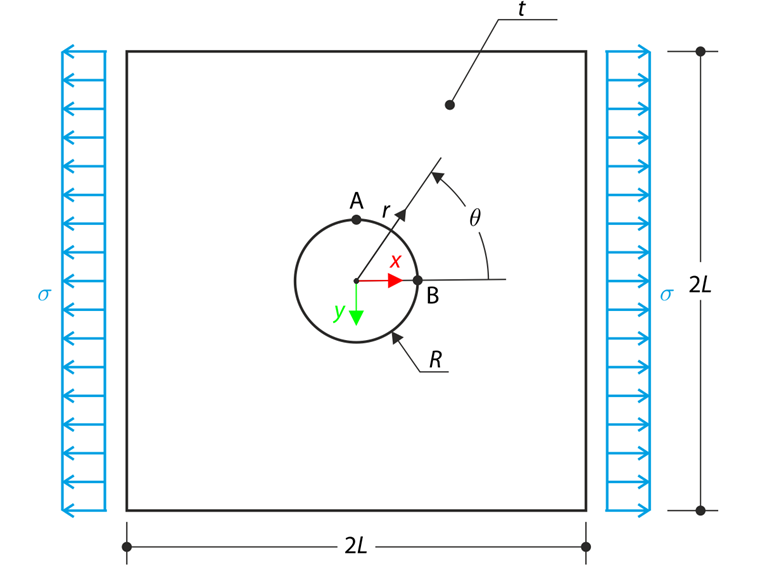
The wide plate with a hole is loaded in one direction by means of the tensile stress σ according to the following sketch. The plate width is large with respect to the hole radius and it is very thin, considering the state of the plane stress.
| Material | Steel | Modulus of Elasticity | E | 210000.000 | MPa |
| Poisson's Ratio | ν | 0.270 | - | ||
| Geometry | Plate Width | 2L | 800.000 | mm | |
| Plate Thickness | t | 1.000 | mm | ||
| Hole Radius | R | 20.000 | mm | ||
| Load | Tension | σ | 100.000 | MPa | |
Determine the radial stress σr, tangential stress σθ, and shear stress τrθ in test points A and B according to Figure 1. The plate is considering infinite wide. Thus the plate modeled in RFEM 5 and RFEM 6 is relatively large.
Analytical Solution
The analytical solution of the stress state can be determined by means of the Airy stress function Φ, which is defined in the state of plane stress. The Airy stress function Φ in polar coordinates is defined as follows:
The radial stress σr and tangential stress σθ in the hole proximity result as follows:
The specific results for test points A and B are listed in the result table below.
RFEM Settings
- Modeled in RFEM 5.05 and RFEM 6.01
- The global element size is lFE = 0.005 m
- The mesh refinement (circular) is used, lFE = 0.001 m
- Geometrically linear analysis is considered
- The number of increments is 5
- Plate entity is used
Results
| Test Point A | Analytical Solution | RFEM 5 | Ratio | RFEM 6 | Ratio |
| σr [MPa] | 0.000 | 2.449 | - | 2.632 | - |
| σθ [MPa] | 300.000 | 300.529 | 1.002 | 300.753 | 1.003 |
| τrθ [MPa] | 0.000 | -0.002 | - | -0.001 | - |
| Test Point B | Analytical Solution | RFEM 5 | Ratio | RFEM 6 | Ratio |
| σr [MPa] | 0.000 | -1.753 | - | -1.828 | - |
| σθ [MPa] | -100.000 | -100.216 | 1.002 | -100.398 | 1.004 |
| τrθ [MPa] | 0.000 | 0.000 | - | 0.000 | - |
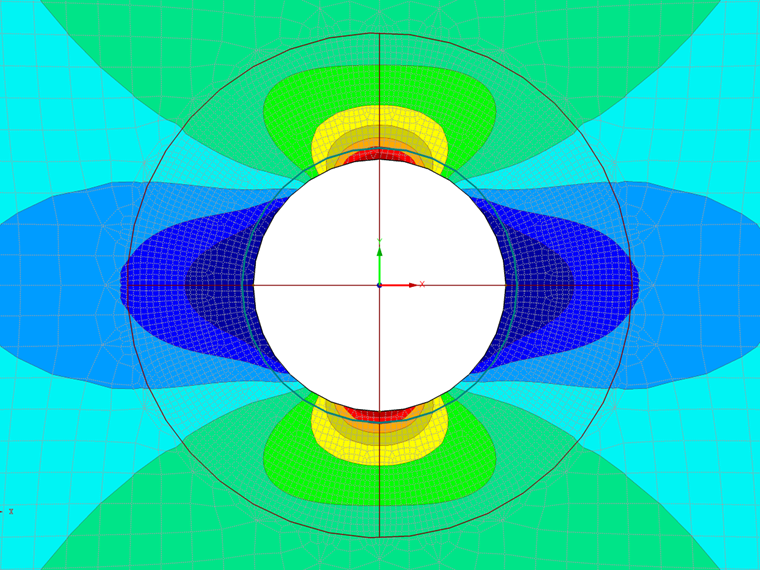
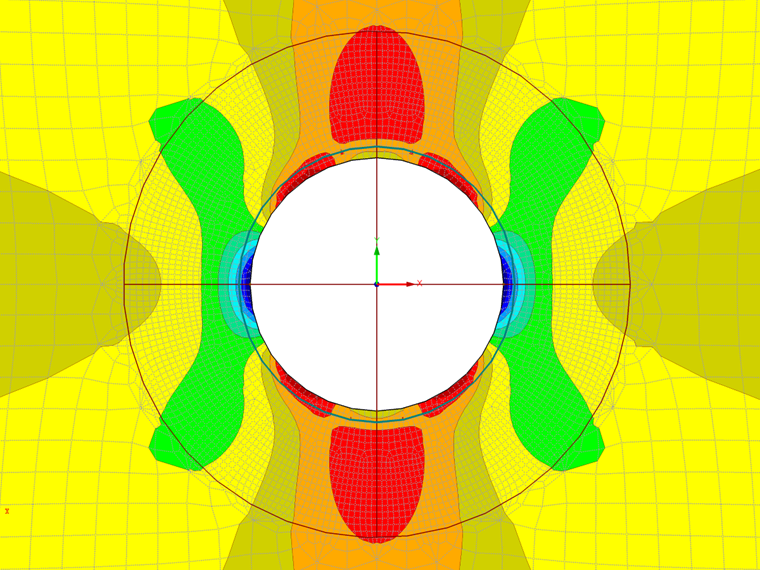
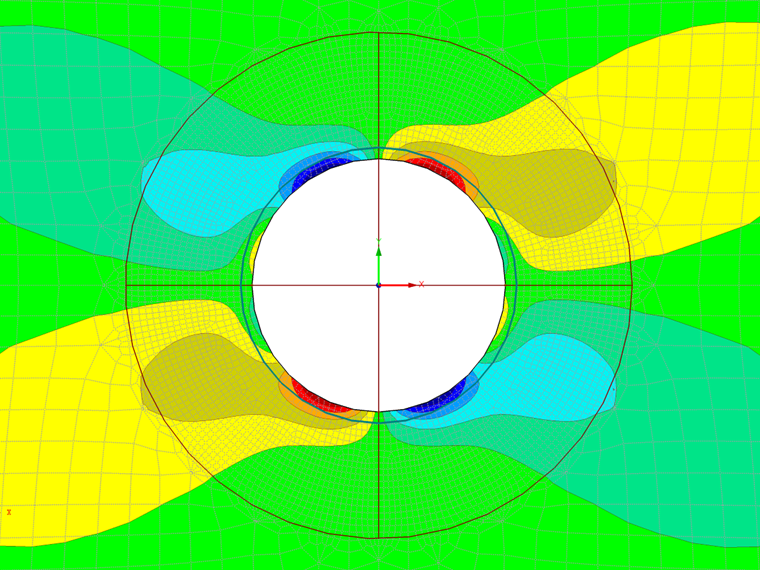
The resultant stress fields around the hole are demonstrated in the following figures. In RFEM 5 and RFEM 6, the values of stresses σr,σθ, and τrθ are read from the values of σx, σy, and τxy in the appropriate point and directions.
Dlubal_KohlA_]_LI.jpg?mw=350&hash=ee8d38f1c4853d80307fa156c159b5e78a3fdca9)
