The following programs and add-ons are particularly suitable for structural timber projects.
Main Program
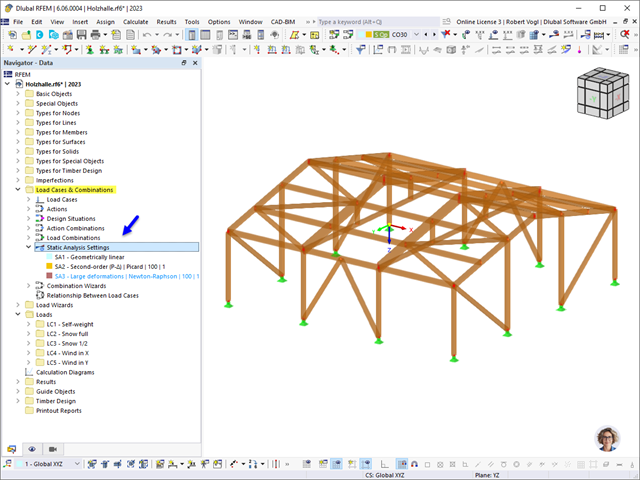
To model your structure and determine the internal forces, you need one of the main programs. Depending on the application area, you can use RFEM 6 or RSTAB 9.
- RSTAB: Analysis of planar or spatial frame & truss structures
- RFEM: Finite element analysis of plate, wall, shell, and member structures
If your model has surface components, such as plates and walls, in addition to membe elements, you need RFEM. This program is the only one with the capability to analyze laminate or cross-laminated timber elements and curved objects.
Timber Design Add-on
Use the Timber Design add-on to design the timber components of your model. The design checks in compliance with specific standards cover both members (bending beams, columns) and surfaces (plates, walls). For columns, the stability analysis according to the equivalent member method or the second order analysis is performed.
You can perform the ultimate and serviceability limit state design checks, as well as the fire resistance design according to the following standards:
- EN 1995 – including National Annexes
- SIA 265
- NTC
- NDS
- CSA O86
- GB 50005
- AS 1720
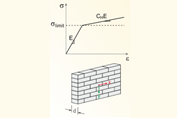
In the fire resistance design, the charring of a cross-section is taken into account for both the stiffness and the design.
Multilayer Surfaces Add-On
With the Multilayer Surfaces add-on for RFEM, you can analyze laminate and sandwich structures with user-defined layer structures. This allows you to design cross-laminated timber panels, for example.
If certain layers have nonlinear material behavior, you can assign the appropriate properties to them. Furthermore, this add-on allows provides you with the option to analyze curved surfaces.
Additional Add-ons
In case of special requirements for your timber structure, we recommend further add-ons and additional programs to help you solve the task.
If you need to perform seismic or vibration analysis, the dynamic analysis add-ons provide you with powerful tools for your structural analysis and design. The Modal Analysis add-on enables the calculation of natural frequencies, and in combination with the Response Spectrum Analysis add-on, you can also perform seismic analysis according to numerous standards.
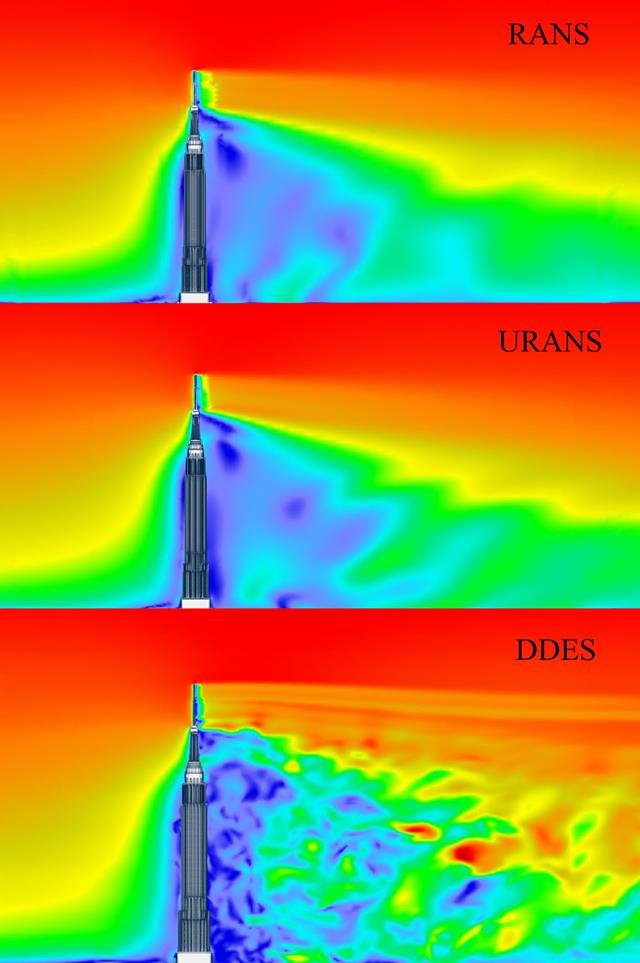
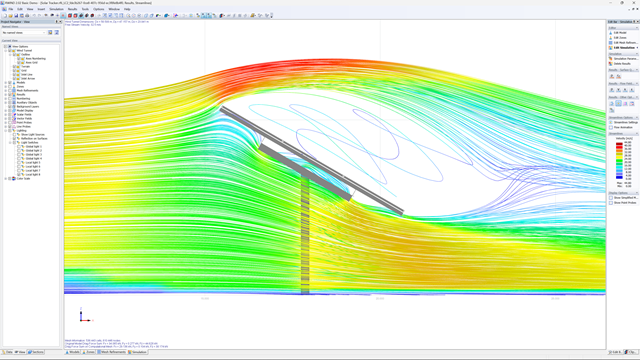
If you are designing a building with a complicated shape, so that the determination of wind loads according to the relevant standards reaches its limits, the RWIND RWIND program will help you: Using a CFD analysis, you can determine the wind loads even for highly complex building shapes.
If the construction stages affect the final internal forces in a structure, or if the governing internal forces for the structural design result from certain construction stages, you should consider the modeling using the Construction Stages Analysis add-on. The Building Model add-on allows you to easily enter large multi-story timber structures.
Show more