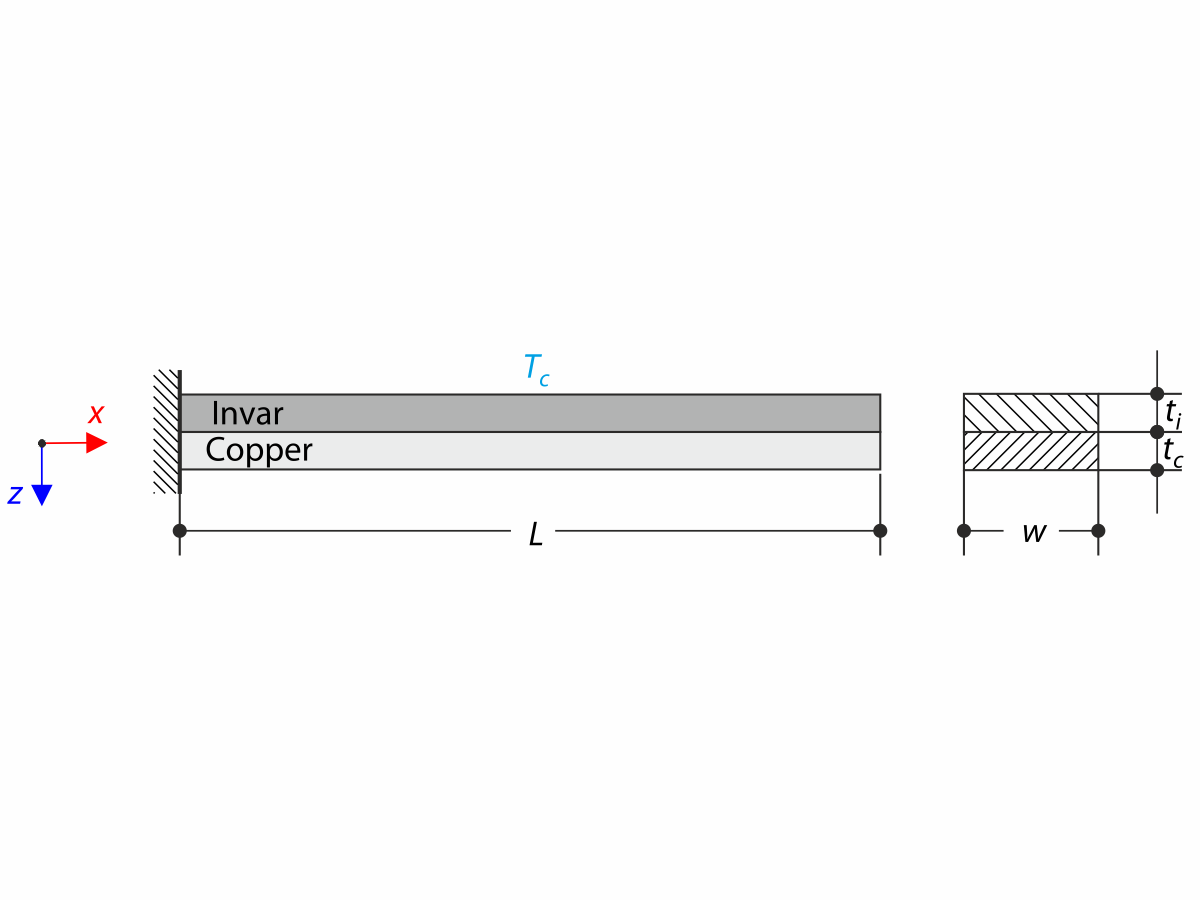
VE0078 | Bimetallic Strip

Description

The bimetallic strip is composed of invar (an alloy of iron and nickel with a very low coefficient of thermal expansion) and copper. The left end of the bimetallic strip is fixed and the right end is free, loaded by temperature difference T_c according to the following sketch. While neglecting the self-weight, determine the deflection u_z,max of the bimetallic strip (free end). The problem is described by the following set of parameters.

Material	Invar	Modulus of Elasticity	E_i	137000.000	MPa
		Poisson's Ratio	ν_i	0.280	-
		Coefficient of Thermal Expansion	α_i	1,200 e-6	°C^-1
	Copper	Modulus of Elasticity	E_c	130000.000	MPa
		Poisson's Ratio	ν_c	0.354	-
		Coefficient of Thermal Expansion	α_c	2 e-5	°C^-1
Geometry		Cross-Section Width	w	5.000	mm
		Layer Thickness	t=t_i=t_c	1.000	mm
		Length	L	100.000	mm
Load		Thermal Loading	T_c	100.000	°C

Bimetallic Strip

Analytical Solution

The bimetallic strip is made of two metals with different coefficients of thermal expansion. They are frequently used in instruments to sense or control temperatures. When the ambient temperature changes, the bimetallic strip bends. This bending is caused by the different elongations of the metals used.

The analytical solution is based on the approach introduced in the reference listed below. The following formula gives the dimensionless coefficient K₁, which can be used for the calculation of the equivalent stiffness.

K_{1} = 4 + 6 \frac{t_{c}}{t_{i}} + 4 {(\frac{t_{c}}{t_{i}})}^{2} + \frac{E_{c}}{E_{i}} {(\frac{t_{c}}{t_{i}})}^{3} + \frac{E_{i} t_{i}}{E_{c} t_{c}} .

Dimensionless Coefficient of Equivalent Stiffness

The maximum deflection of the bimetallic strip is then defined by the following formula:

u_{z, max} = \frac{6 (α_{i} - α_{c}) (t_{i} + t_{c}) T_{c}}{t_{s}^{2} K_{1}} \frac{L^{2}}{2} \approx - 7.049 m m .

Maximum Deflection of the Bimetallic Strip

RFEM Settings

Modeled in version RFEM 5.26 and RFEM 6.06
The element size is l_FE= 0.250 mm
Geometrically linear analysis is considered
Isotropic linear elastic material model is used

Results

Model	Analytical Solution	RFEM 6		RFEM 5
Model	u_z,max [mm]	u_z,max [mm]	Ratio [-]	u_z,max [mm]	Ratio [-]
Plate	-7.049	-7.047	1.000	-7.047	1.000
Solid	-7.049	-6.956	0.987	-7.064	1.002

807x

20x

Verification Example 000078 | 1

References

YOUNG, W., BUDYNAS, R., & SADEGH, A. (2011). Roark's Formulas for Stress and Strain (8th edition). McGraw-Hill Education.

;