La scheda Smorzamento offre varie opzioni di impostazione per considerare lo smorzamento strutturale viscoso nell'analisi utilizzando l'analisi time history lineare.
smorzamento
Nel manuale è l'analisi di Newmark lineare implicita, è disponibile solo il 'Tipo di smorzamento'Rayleigh. Per il metodo di analisi modale lineare, invece, l'elenco offre due opzioni:
- Smorzamento di Lehr | Constante
- Rayleigh
Quando si applica lo smorzamento di Rayleigh a un'analisi modale lineare, i coefficienti di smorzamento di Rayleigh α e β vengono convertiti nei valori di smorzamento di Lehr's, Di, (vedi Parameters). La soluzione è quindi unica.
Nel caso dello smorzamento di Rayleigh, è possibile determinare i parametri di smorzamento automaticamente dallo smorzamento di Lehr's. Selezionare la casella di controllo 'Calcolo dallo smorzamento di Lehr's'. Quindi, inserisci i parametri delle due forme modali più dominanti per le 'frequenze naturali' f1 e f2 del modello con i valori corrispondenti per lo smorzamento di 'Lehr's' D1 e D2.
Nella sezione inferiore, viene visualizzato il 'Diagramma Frequenze naturali - Smorzamento' per lo smorzamento di Rayleigh. Rappresenta il rapporto disponibile tra la frequenza angolare naturale e la costante di smorzamento di Lehr's.
Parametri
In questa sezione di dialogo, è possibile definire i parametri dello smorzamento. Differiscono a seconda del tipo di smorzamento.
Smorzamento di Lehr
Lo smorzamento di Lehr's è definito dalla costante di smorzamento di ' Lehr's' D. È definito per ogni singola forma i come un coefficiente tra lo smorzamento esistente e lo smorzamento critico come segue:
| Ci | Entrate nella matrice di smorzamento diagonale |
| mi | Masse modali |
| ωi | Frequenze angolari del sistema strutturale |
La matrice di smorzamento C deve essere una matrice diagonale.
Rayleigh
La matrice di smorzamento dello smorzamento di Rayleigh è definita mediante i due parametri di smorzamento α e β come segue:
| C | Matrice di smorzamento |
| M | Matrice di massa |
| K | Matrice di rigidezza statica |
La matrice di smorzamento C non deve essere necessariamente una matrice diagonale per l'analisi time history diretta. Ad esempio, puoi trovare ulteriori informazioni sullo smorzamento di Rayleigh in [1].
La seguente relazione esiste tra i coefficienti di Rayleigh e lo smorzamento di Lehr's:
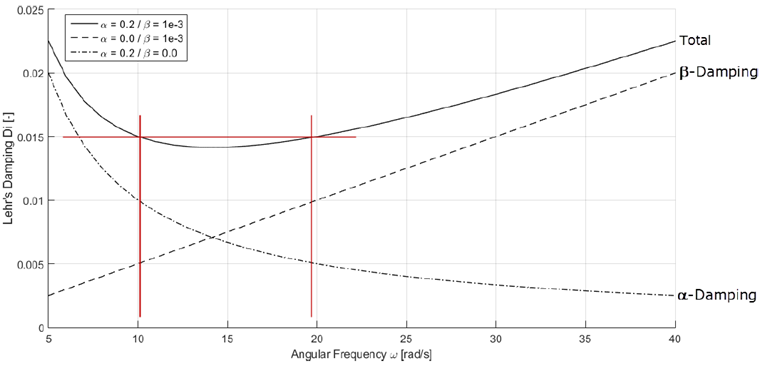
Questa equazione è visualizzata nel grafico seguente. Vengono considerate diverse costellazioni per i parametri di smorzamento α = 0.2 e β = 0.001.
Per ogni coppia di coefficienti di Rayleigh risultano diversi valori di smorzamento di Lehr's. Dipendono dalla frequenza angolare.